Gleeble试验中再热裂纹敏感性评价方法探讨

(合肥通用机械研究院有限公司，合肥 230031)

0 引言

再热裂纹是Cr-Mo钢压力容器安全使用的威胁之一[1-3]，早在20世纪70年代，我国压力容器学会就牵头组织国内15个单位，采用6种方法对10种压力容器用钢进行再热裂纹敏感性的试验研究[4]。随着改进型含V的Cr-Mo钢的研发和使用，其再热裂纹倾向更为突出，20世纪80年代，西安交通大学在插销试验中利用X-Y记录仪记录的载荷-位移曲线计算塑断功，以此评价其再热裂纹敏感性[5]。20世纪初期，中国一重结合加氢设备的制造，采用多种方法对加钒钢及其焊材进行再热裂纹试验，并按API-A附录B的要求作筛选[6]。

Gleeble试验是对一定直径的试样进行高温缓慢拉伸，在试样断裂后，测量断口上3个截面的直径，计算断面收缩率来评价再热裂纹敏感性。近年来，国内外已有多篇关于再热裂纹Gleeble试验的报道[7-10]，在这些研究中，均是采用断面收缩率(ROA)作为参量来评价材料的再热裂纹敏感性。笔者在试验过程中，发现作为主要依据的断面收缩率，其测量并不可靠，由于Gleeble试验是采用试样本身的电阻热对试验部位加热，在试样断裂瞬间产生电弧，局部会发生熔化，断口位置的电流很大，导致不规则的断口截面难以准确测量(见图1)，受人为因素影响且评定结果容易产生争议。

图1 再热裂纹筛选试样试验后的断口形貌

而在Gleeble试验中，若利用试验机记录的载荷-位移曲线，计算载荷对位移的积分，得到试验从开始拉伸到断裂全过程所消耗的功，可以定量评价材料抗变形的能力，这在早期的类似试验中都有采用，能否在Gleeble试验中利用此变量来判断材料的再热裂纹敏感性?在焊缝金属或熔敷金属的再热裂纹筛选试验中采用内积功作为评价指标，可以客观地反映其再热裂纹敏感性。本文试图对此进行探索研究。

1 试验用材料和试验方法

1.1 试验用材料

本次试验采用厚度为280 m的2.25Cr-1Mo-0.25V钢锻件，供货状态为正火+回火，其化学成分和力学性能分别见表1,2。

表1试验用材料的化学成分%

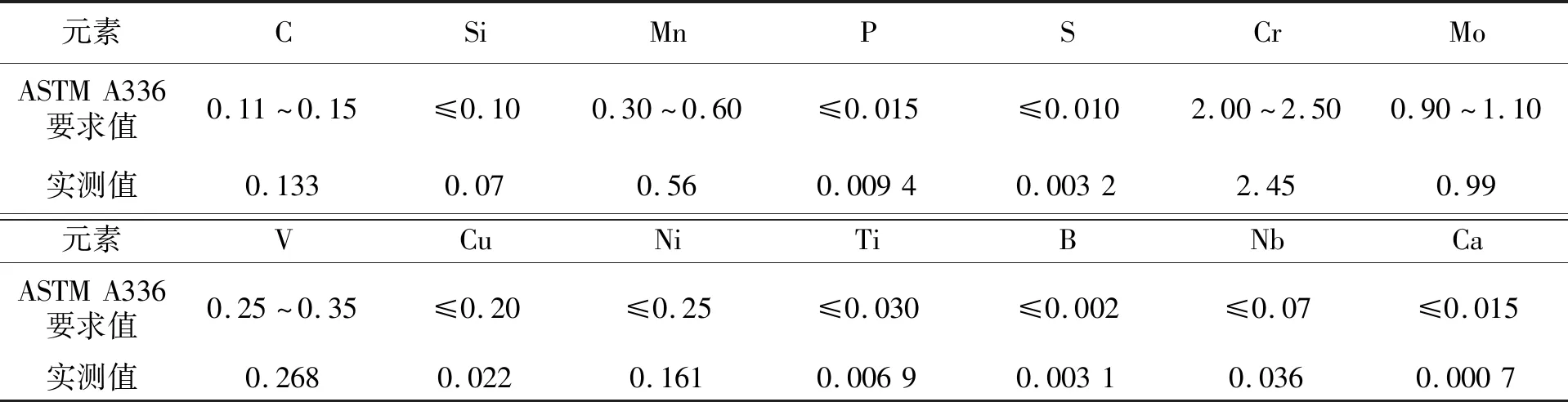
元素CSiMnPSCrMoASTMA336要求值0.11～0.15≤0.100.30～0.60≤0.015≤0.0102.00～2.500.90～1.10实测值0.1330.070.560.00940.00322.450.99元素VCuNiTiBNbCaASTMA336要求值0.25～0.35≤0.20≤0.25≤0.030≤0.002≤0.07≤0.015实测值0.2680.0220.1610.00690.00310.0360.0007

表2 试验用材料的力学性能

试验采用规格为∅4.0 mm、牌号US-521H的埋弧焊丝，配套焊剂牌号为PF-500，符合JIS Z3352 SACG1的要求。

1.2 再热裂纹Gleeble试验程序

对母材进行试验时，先对试样进行焊接热循环的模拟[8]，然后再进行再热裂纹Gleeble试验；而对焊缝金属则直接进行Gleeble试验。Gleeble试验程序和试验过程曲线与文献[8]相同。

1.3 内积功计算方法

试验过程中采用的是恒速拉伸直至试样断裂，其载荷与变形的关系如图2所示。

针对试验过程中某点D而言，其与上一时间点C组成的ABCD包围的面积S可简化计算如下：

Si=0.5(Pi-Pi-1)(Xi-Xi-1)

(1)

W=S0+S1+……

(2)

式中P——载荷，N；

X——变形量，mm；

W——内积功，N·mm。

图2 载荷与变形的关系示意

面积S表示在试样变形从X1到X2期间，试验装置对试样所做的功，对整个拉伸过程进行积分，得到的值即为在整个拉伸过程中试样变形所做的功Wt，在此称为内积功。内积功在一定程度上反映试样在高温拉伸过程中承受变形的能力，也可以看成反映材料抗再热裂纹的能力。

打开Gleeble试验机所记录的试验数据文件，可以看到试验机所记录的数据结构，如表3所示。

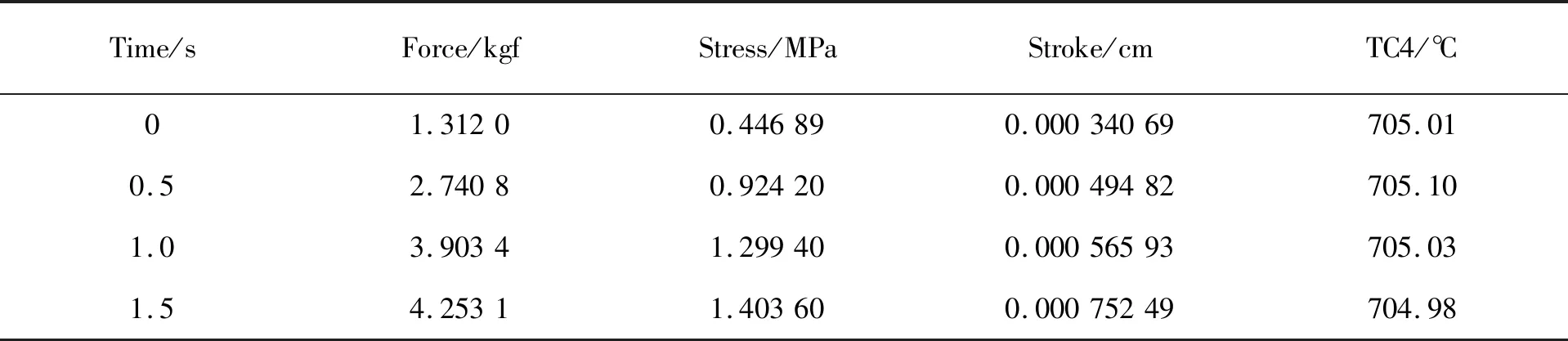
表3 Gleeble试验机记录的试验数据结构

其中,time(sec)为试验时间计时，force(kgf)为载荷，stroke(cm)为变形，TC4(℃)为温度。由于试验数据量较大，为处理该数据，编制了一个试验数据处理程序，程序框图见图3。程序首先计算屈服强度，得到变形的起始位置X0，将指针移至X0，读取force字段和stroke字段的数据作为初值，然后指针加1，读取第2个数据。按式(1),(2)计算当前内积功，继续指针加1，读取第3个数据，计算当前内积功，并与上次内积功合并，得到当前累积的内积功，依次类推，直至全部数据处理完，最后得到本次试验的内积功W。

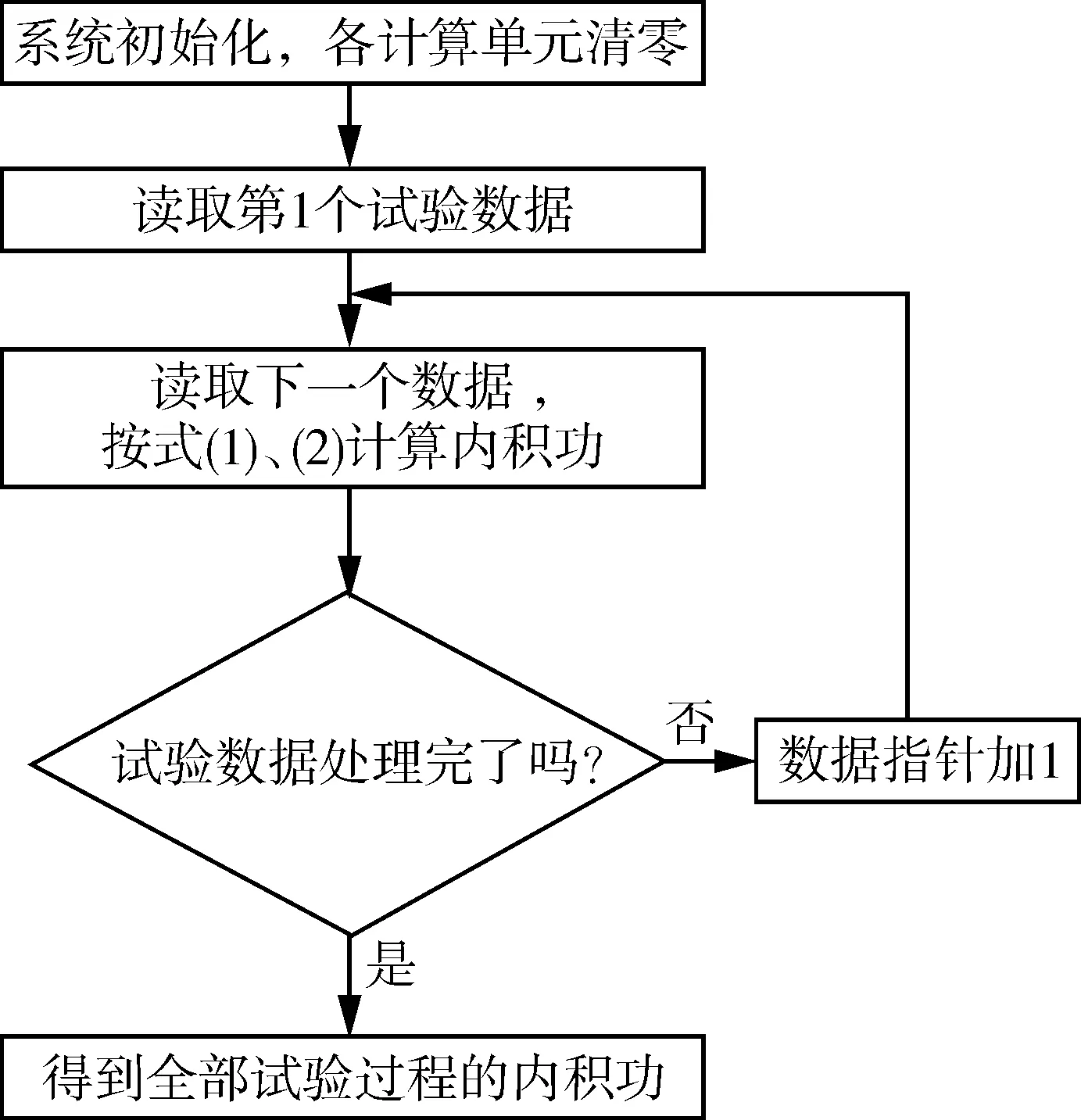
图3 由Gleeble试验数据计算内积功框图

2 试验结果及讨论

2.1 Gleeble试验中的内积功与插销试验结果的对比

2.25Cr-1Mo-0.25V钢的Gleeble试验结果处理时采用内积功作为参量，与插销试验的结果[10]进行对比，结果见图4。可以看出，随着试验温度的升高，其内积功和插销试验的断裂时间均呈现先降低、后升高的趋势，两种方法测得的2.25Cr-1Mo-0.25V钢锻件的再热裂纹“C”形曲线十分接近，敏感温度基本相同，均在690 ℃左右。

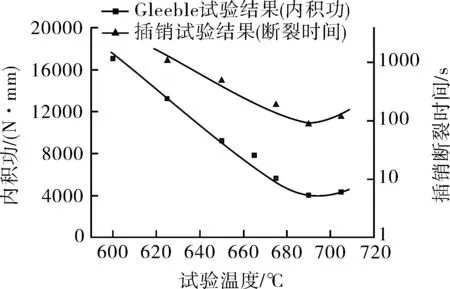
图4 Gleeble试验与插销试验的结果对比

2.2 Gleeble试验中的内积功与断面收缩率的对比

在Gleeble试验中分别以内积功和断面收缩率(ROA)为参量对试验结果进行处理，分别对2.25Cr-1Mo-0.25V钢及其焊缝金属进行再热裂纹敏感温度的测量，其中，焊缝金属试验数据与比利时焊接研究所(BWI)的试验结果[11]进行对比，见图5,6。

图5 Gleeble试验中内积功与ROA对比

由图5,6可以看出，Gleeble试验得到内积功和ROA作为参量的试验结果基本一致，其再热裂纹敏感温度也相同，其中2.25Cr-1Mo-0.25V钢焊缝金属采用内积功的结果与本次试验采用ROA及国外试验结果有很好的对应关系，说明Gleeble试验可采用内积功参量测试材料的再热裂纹敏感温度。

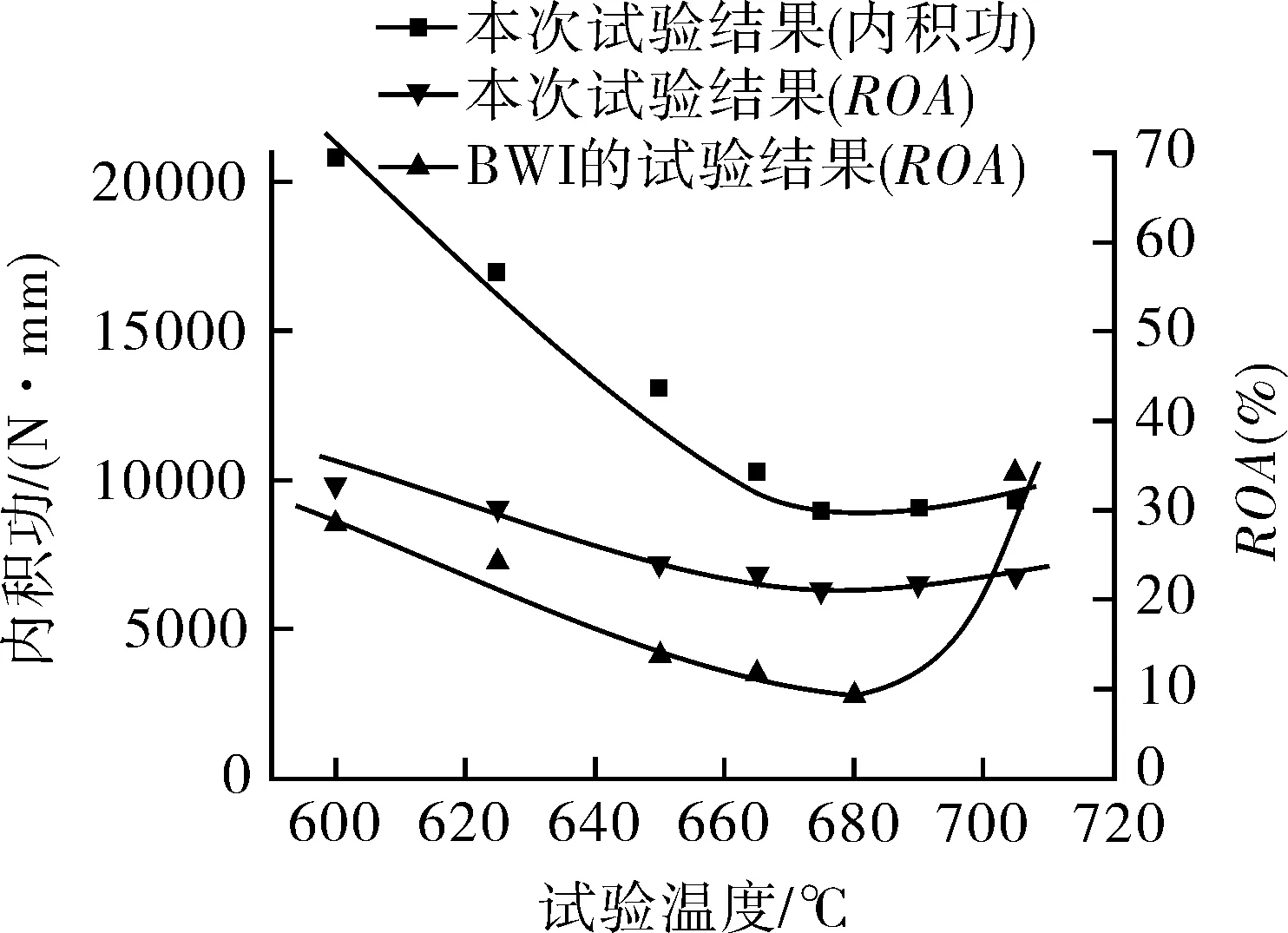
图6 焊缝金属Gleeble试验中内积功与ROA对比

2.3 Gleeble试验中采用内积功作为再热裂纹评价的可行性分析

断面收缩率是衡量材料塑性变形能力的指标，Gleeble再热裂纹试验中，采用试样拉断时断裂部位的截面积与原始截面积之差，除以原始截面积之商的百分数即为断面收缩率。断面收缩率越小，说明拉伸过程中仅发生少量的变形即发生断裂，材料高温下抵抗变形的能力较差，对再热裂纹敏感性高。所以，断面收缩率一定程度上可以反映材料的再热裂纹敏感性。

内积功是将Gleeble高温拉伸过程中的载荷对位移进行积分，其表征的是材料在高温下抵抗变形的能力。随着试验温度的提高，材料的强度下降，拉伸载荷相对较低，载荷对位移积分所得到的内积功呈下降趋势；在再热裂纹敏感温度附近，晶界强度低于晶内强度，拉伸产生的变形主要集中于晶界，随着拉伸应力的持续，相对弱化的晶界首先产生空穴，且空穴长大逐渐形成微裂纹。若继续拉伸，裂纹会快速扩展，直至断裂，在敏感温度附近，由于断裂时间缩短，实际计算的内积功较小。

当试验温度升高后，晶界与晶内强度趋于一致，材料抗高温变形能力增加，虽然载荷有所下降，但断裂时间延长，积分得到的内积功有所增加，在试验温度范围内得到一种“C”形曲线，对应最小内积功的温度为再热裂纹敏感温度。由于内积功反映的是HAZ粗晶区在不同温度下的塑性储备，相对而言，采用内积功更能准确反映材料的再热裂纹敏感性[12]。对前期SA543钢Gleeble再热裂纹试验过程数据进行处理，采用内积功作为参量的再热裂纹“C”形曲线与插销试验的结果[13]进行对比如图7所示，可以看出，采用内积功参量测得的再热裂纹敏感温度也与插销试验结果吻合。这说明，不同的材料均可采用内积功参量来测试其再热裂纹敏感温度。

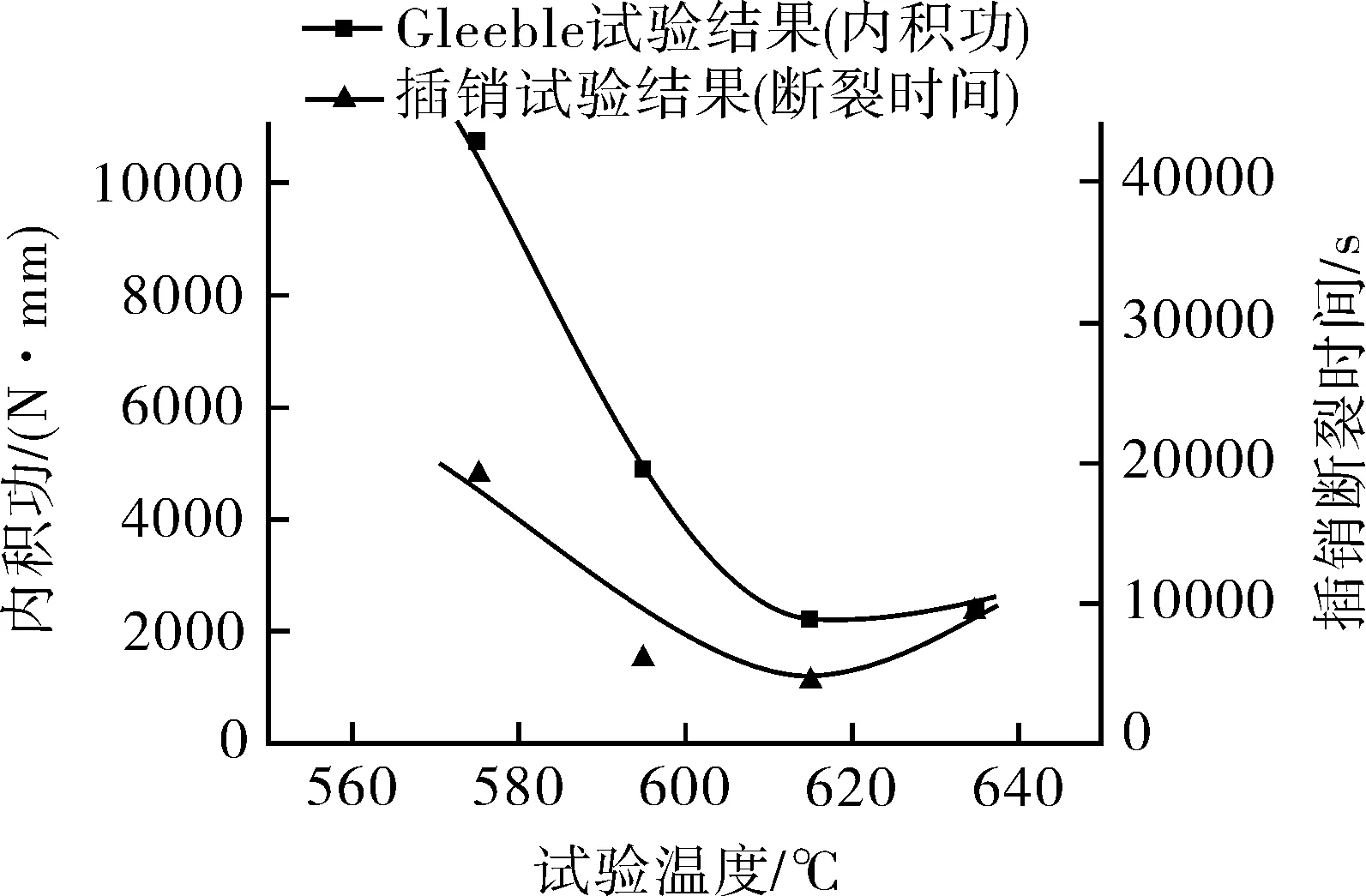
图7 SA543钢Gleeble试验结果与插销试验对比

目前各种材料的Gleeble试验数据较少，以现存的试验数据提出内积功的再热裂纹敏感性判据尚不严密。可先参照ROA判据间接推算内积功的判据，例如2.25Cr-1Mo-0.25V钢的Gleeble试验内积功与ROA的对应关系(见图8)。

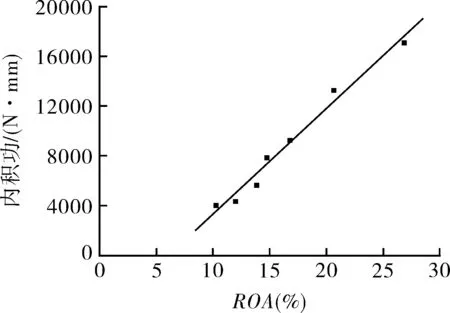
图8 Gleeble试验中内积功与ROA的对应关系

对图8中的数据进行线性拟合，得到2.25Cr-1Mo-0.25V钢的Gleeble试验中内积功与ROA的关系式如下：

内积功=850×ROA-5240

(3)

一般认为，当ROA<20%时，认为该材料对再热裂纹敏感。这样，ROA=20%，按式(3)计算得对应的内积功为11 760 N·mm，则可以认为当内积功大于11 760 N·mm时，该材料对再热裂纹不敏感，反之，则对再热裂纹敏感。本次试验中敏感温度下的内积功为3 398 N·mm，可见该材料有一定的再热裂纹敏感性，这与插销试验的结果基本吻合[10]。

在相同的试验条件下，内积功受材料高温强度的影响，若采用内积功来衡量再热裂纹敏感性需考虑材料高温强度的影响，也可将内积功折合成最大残余应力(约为高温屈服强度的80%)下的变形量来比较，此项工作尚需诸多的试验研究以及大量的工程积累，才能准确地评价材料的再热裂纹敏感性，并避免再热裂纹的产生。

3 结论

(1)对Gleeble试验过程中的载荷对位移的积分，可得到内积功参数。通过2.25Cr-1Mo-0.25V钢材和焊缝金属以及SA543钢的Gleeble试验数据处理表明：采用内积功来测试材料的再热裂纹敏感温度是可行的。

(2)通过对ROA值与内积功值对应关系的分析，可以采用现行评价再热裂纹敏感性的ROA判据来推算内积功临界值，随着试验数据的积累，期望得到更加准确的内积功判据来评价材料的再热裂纹敏感性。