内压标准椭圆封头弹塑性屈曲分析及失效载荷研究

(南京工业大学 机械与动力工程学院，南京 211816)

0 引言

椭圆封头由于其椭球部分经线曲率变化平滑连续，应力分布比较均匀，且易于冲压成型，是目前中、低压容器中应用最为广泛的封头之一。椭圆封头内压弹性屈曲研究始于20世纪50年代。Galletly[1]针对一大直径硫化焦化器在静水压力试验时发生的屈曲失效进行了线弹性分析，发现椭圆封头过渡段呈受压状态;随后，Bushnell等[2-3]对内压作用下椭圆封头的弹性屈曲载荷进行了研究;为防止在椭圆封头转角区域的周向应力造成失稳,Shield等[4]给出了椭圆封头的弹性屈曲载荷。参照文献[4]等研究成果，我国GB 150—2011[5]中规定，为防止内压下的弹性失稳，标准椭圆形封头的有效厚度应不小于封头内直径的0.15%(非标准椭圆封头为0.3%)。徐思浩[6]基于文献[4]及WRC Bulletin提供的凸形封头弹性失稳压力表达式，针对几组常用材料，对不同径厚比下椭圆封头的弹性屈曲载荷和强度失效载荷进行比较，认为GB 150—2011对椭圆封头内压失稳的规定不够全面，值得进一步研究。

随着有限元技术及数值模拟软件的发展，大量学者对凸形封头的弹塑性屈曲行为进行数值模拟。Bushnell等[7-9]运用BOSOR5有限元程序分析内压下碟形封头的屈曲载荷，并与试验结果[10-12]进行比较。Galletly等[13]对内压作用下碟形封头进行弹塑性屈曲试验研究，通过探针得到了过渡段的变形曲线，成功地获得了屈曲行为。周益[14]通过内压试验、形貌扫描以及数值模拟等研究工作,获得了椭圆封头与筒节过渡段变形规律，数值模拟结果与试验结果较为一致。陶伟明等[15]采用有限元软件ABAQUS分析了碟形封头过渡区局部塑性屈曲问题，并提出应尽可能地测量结构的真实几何形状和缺陷，才能保证模拟结果与试验相接近。张彤等[16-17]基于ABAQUS对内压碟形封头进行了非线性屈曲分析，其计算得到的临界屈曲载荷与前人试验结果接近，捕捉了完整的屈曲及后屈曲路径和形态。

本文采用有限元弹塑性分析，较为系统地讨论不同材料及不同厚径比δe/Di下标准椭圆封头分析结构内压屈曲载荷Pcr及极限载荷PL的变化规律，并与现行标准GB 150—2011[5]中的规定进行比较分析。本文结果可为内压薄壁标准椭圆封头设计准则提供指导。

1 碟形封头屈曲载荷的有限元验证

采用ANSYS软件中弧长法对某碟形封头进行弹塑性屈曲分析，碟形封头尺寸参照文献[13]，对封头过渡区周向受压区局部引入以下几何初始缺陷，计算分析屈曲载荷。

1.1 厚度缺陷施加

对于实际结构屈曲问题，由于在屈曲点处的不连续效应，导致问题无法直接求解。所以，往往通过引入初始扰动实现。本文通过对封头局部过渡区引入初始厚度缺陷扰动，使得屈曲点处的不连续响应转化为连续响应。根据封头制造规定GB/T 25198—2010[18]，初始厚度缺陷取极限情况下厚度减薄15%计算[19]。

实际封头结构中存在的缺陷是随机的，为比较不同方式构建的缺陷对屈曲载荷Pcr的影响，下面的算例中在过渡区设置了不同缺陷布置样式：(1)单个缺陷；(2)相邻45°布置2个缺陷；(3)相邻90°布置2个缺陷；(4)过渡区圆周一圈缺陷。

1.2 单元类型及边界条件

选用8节点有限元壳单元Shell 181对有限元模型进行划分网格，并对网格进行无关性验证，Shell 181 单元的有效可靠性在文献[20]中已有详细说明。椭圆封头模型边界条件为模型柱壳底部采用固定约束，封头内表面承受均匀内压。

1.3 材料本构模型

比较文献[21]中Ramberg-Osgood材料强化模型与理想弹塑性材料模型对封头内压屈曲载荷的影响，结果表明影响不显著。本文选用理想弹塑性本构模型进行有限元模拟计算。4种缺陷方式下碟形封头弹塑性屈曲载荷见表1。

由表1可以看出，不同缺陷布置方式得到的屈曲载荷存在差异，缺陷布置范围越大，计算得到的屈曲载荷越小。但各组屈曲载荷值相差较小，与试验结果误差最大仅为6.90%。考虑到单个缺陷模型得到的屈曲载荷与试验值最为接近，以下采用单个缺陷布置方式进行计算。

表1 4种缺陷方式下碟形封头弹塑性屈曲载荷

2 标准椭圆封头内压屈曲有限元模型

2.1 材料性能参数

选取几组压力容器常用材料S31603,S30408,Q235B,Q245R,Q345R,13MnNiMoR，常温下所选材料力学性能[5]见表2。

表2 材料参数

2.2 分析模型结构尺寸

2.2.1 不同厚径比

为了研究不同厚径比及材料参数对标准椭圆封头内压屈曲载荷的影响，固定封头内径Di=1 000 mm,通过改变封头的厚径比δe/Di、不同材料参数建立模型进行有限元分析。封头直边段取25 mm，柱壳段取h=55 mm；取厚径比δe/Di=1‰,1.25‰,1.5‰,1.75‰,2‰,2.25‰。

2.2.2 偏差及缺陷

GB 150.4—2011中6.4.2条款规定凸形封头内表面形状偏差，最大形状偏差外凸不得大于1.25%Di,内凹不得大于0.625%Di。为讨论不同偏差类型及偏差量对内压屈曲载荷的影响，参照文献[22-23]中给出的标准椭圆封头最大壁厚减薄位置，分别在标准椭圆封头最大壁厚减薄位置施加不同的形状偏差(最大形状偏差如图1所示)，计算结果见表3。

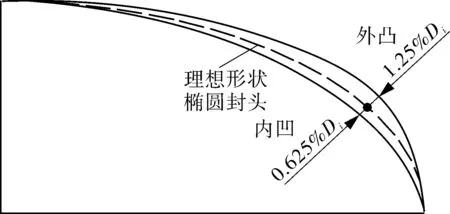
图1 椭圆封头内凹外凸形状偏差

表3 不同形状偏差下标准椭圆封头模型内压屈曲载荷Pcr

可以看出，相同厚径比下，各组计算模型屈曲载荷Pcr随缺陷类型(内凹、外凸)及偏差量大小变化而有所变化，但总体变化量较小，各组最大偏差在2.24%～6.87%。表3结果表明，各组椭圆封头计算模型内凹0.625%下屈曲载荷均小于外凸1.25%下屈曲载荷。为考虑极限工况，文中采用形状偏差内凹0.625%Di的椭圆封头模型，在最大壁厚减薄位置施加单个缺陷厚度减薄15%。

3 标准椭圆封头内压屈曲分析失效载荷

3.1 屈曲行为分析及临界屈曲载荷定义

以厚径比δe/Di=1‰、材料Q345R分析模型为例，对标准椭圆封头进行内压屈曲分析。运用弧长法成功获得其在内压作用下的弹塑性屈曲及后屈曲行为。以下对其进行分析。

图2示出内压为0.542 MPa时椭圆封头分析模型变形图。可以看出，椭圆封头中心区域与柱壳存在不同程度往外扩张，而过渡环壳则向内收缩。由此说明，在内压作用下，虽然结构总体呈向外膨胀的状态，但在过渡段却呈相反的变形，向内凹陷。通过研究该结构特点不难发现，该结构由柱壳与椭球壳两部分组成，这两部分结构由于几何形状不一致而导致变形不一致，因而在均匀内压作用下，柱壳向外扩展的速度与椭球壳向外扩展的速度不一致，结构需要通过过渡段向内凹陷的变形，协调整体的变形。

图2 内压0.542 MPa时分析模型变形图

图3 内压0.542 MPa时分析模型过渡段波状变形图

由图3可以看出，压力容器过渡段出现了波纹状变形，结构从对称变形发展到过渡段的波状变形，这说明结构的平衡路径已经改变。图4示出此时的Mises应力分布，可以明显地看出压力容器的屈曲模态和屈曲时小波的数目。随着内压进一步增加，过渡段将出现凸起的褶皱(如图5所示)，结构开始进入后屈曲阶段。

图4 内压0.542 MPa时分析模型Mises应力分布

图5 内压0.568 MPa时分析模型出现第一个褶皱

取第一个褶皱生成的相邻部位的6个节点(节点位置见图5右上方)，提取节点从开始加载到生成第一个褶皱，变形随载荷的变化曲线。图6示出各节点相应周向位移随载荷的变化曲线。直到加载到一定载荷前，各节点基本保持一致的变形。周向位移为0，说明过渡段周向保持不变。当内压超过一定载荷，各节点曲线开始分离，即节点的变形开始不一致，此时结构变形出现对称的正负增长，结构此时开始发生分叉屈曲。

随着载荷增加到某一时刻，各节点变形分离量突然剧烈增大，对应的压力约为Pcr=0.568 MPa，此时对应着第一个褶皱的完全生成。由此可以发现，从开始出现褶皱，到褶皱完全生成，实际上包含了一段压力范围，即褶皱生成的过程。参考文献[6-7]，本文将结构由对称变形转为非对称变形作为判断压力容器出现分叉屈曲的标志，将分叉屈曲结束时压力作为临界屈曲载荷Pcr的定义。

图6 褶皱处各节点的载荷-位移曲线

3.2 不同厚径比δe/Di下屈曲载荷分析

对不同厚径比δe/Di下标准椭圆封头分析模型进行内压屈曲分析，屈曲载荷Pcr计算结果见表4。

图7示出屈曲载荷Pcr与厚径比δe/Di变化关系。可以看出，屈曲载荷Pcr与厚径比δe/Di之间近似成正比，厚径比δe/Di值越大，屈曲载荷Pcr值越大。

表4 不同厚径比δe/Di下标准椭圆封头模型内压屈曲载荷Pcr

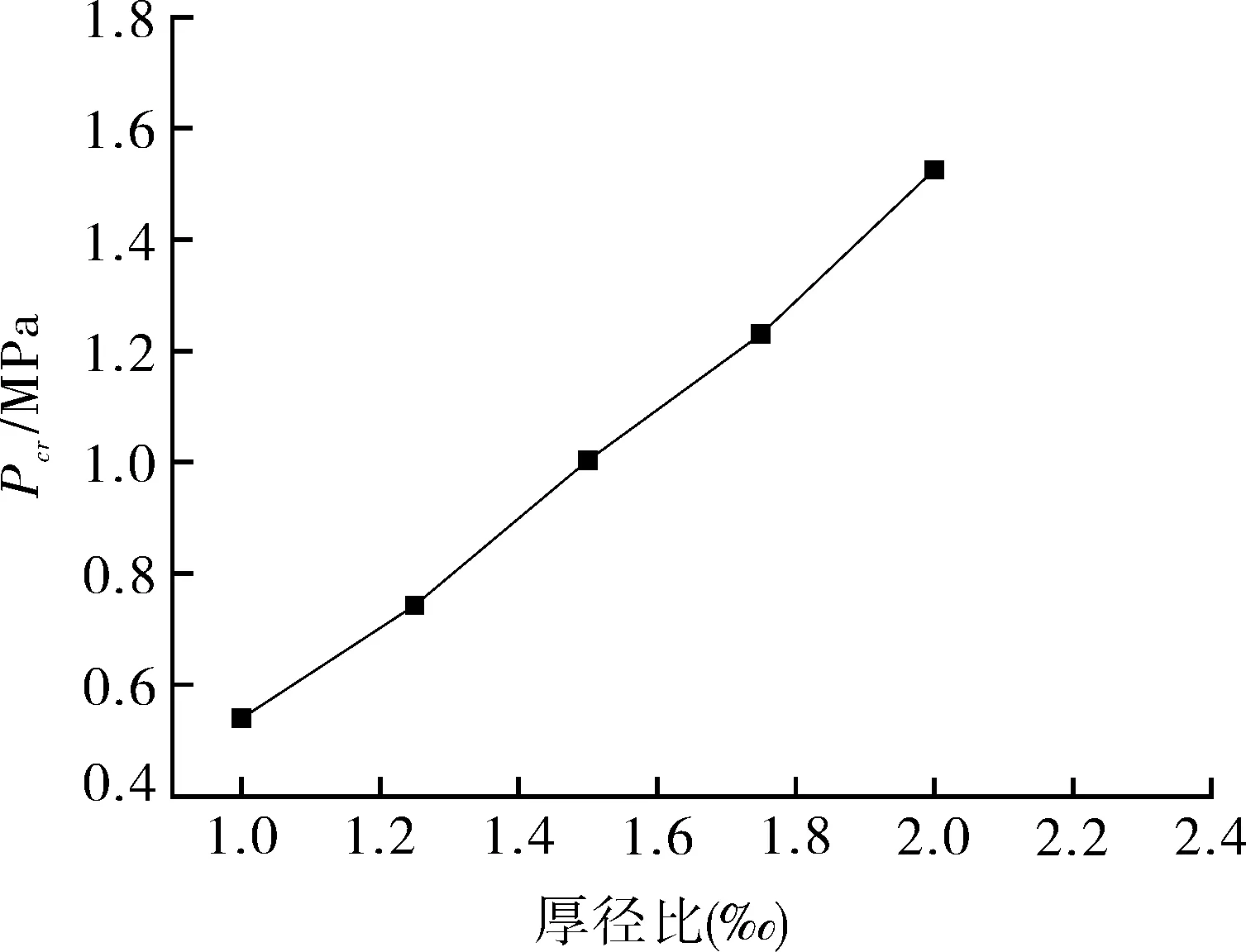
图7 模型临界失稳压力Pcr随厚径比δe/Di变化示意

厚径比δe/Di不仅影响临界载荷大小，同时还影响着屈曲模态。图8～10示出δe/Di=1‰，1.5‰，2.25‰时分析模型的分叉屈曲模态。

(a)Mises应力分布

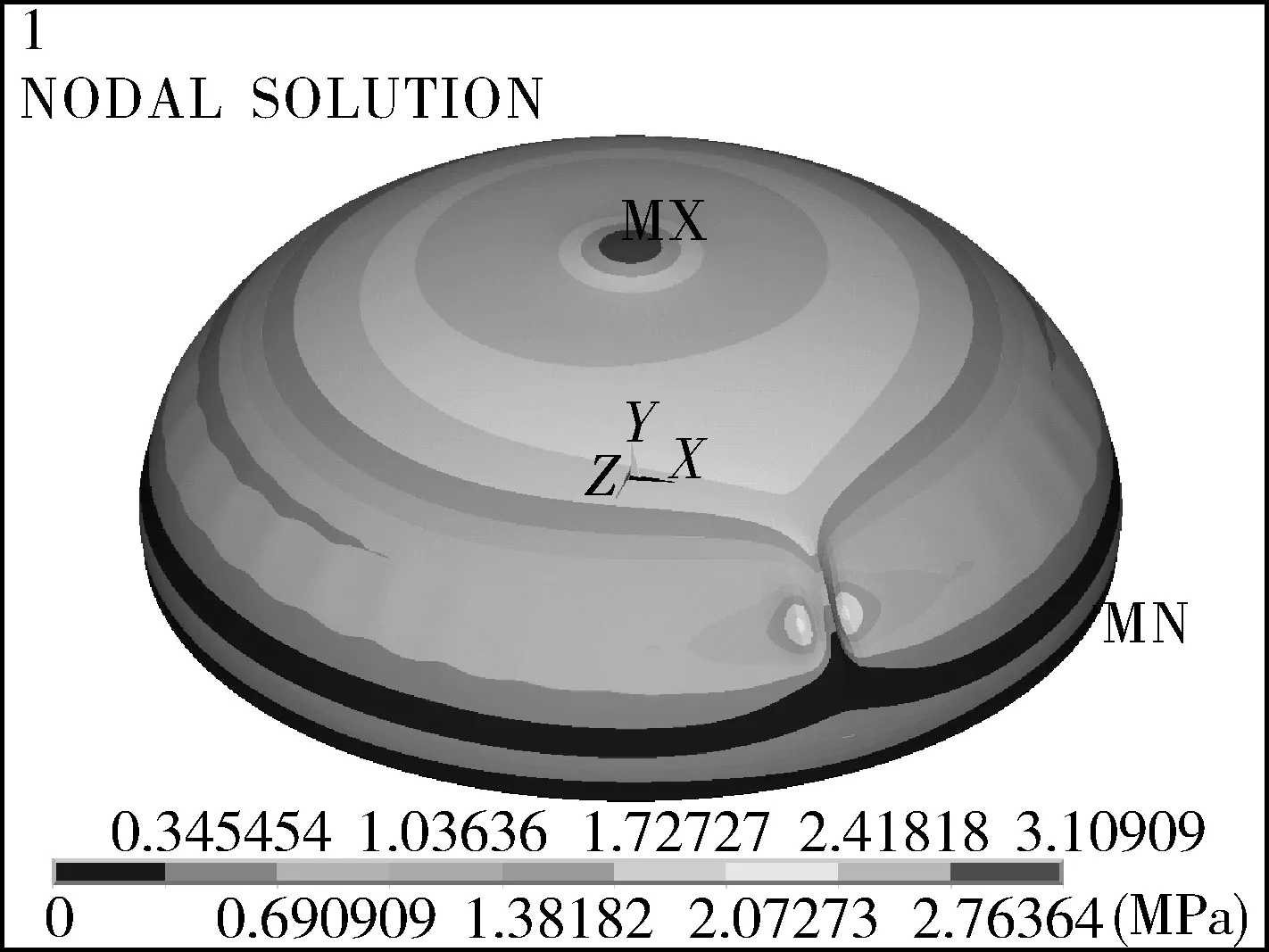
(b)变形图

图8δe/Di=1‰时分析模型的分叉屈曲模态(Pcr=0.568 MPa)

由图8～10可以看出，δe/Di=1‰，1.5‰时，Mises应力的波纹状分布。δe/Di=1‰时波状应力带较为明显；当δe/Di=1.5‰时，波状应力带显示不明显；而当δe/Di=2.25‰时，过渡段的波状应力带已不存在。可见，对于较厚的内压标准椭圆封头模型，并未出现分叉屈曲。可以看出，δe/Di=1‰，1.5‰的模型均在过渡段出现了肉眼可视的褶皱，而δe/Di=2.25‰的模型则没有出现褶皱，结构保持对称的变形。

3.3 极限载荷PL与屈曲载荷Pcr比较

椭圆封头模型在内压作用下主要有两种失效方式：周向屈曲和强度破坏。周向屈曲失效正是前文中重点讨论的分叉屈曲现象，对于强度破坏失效的临界压力，本文称之为极限载荷PL，其值根据载荷-位移曲线，采用两倍弹性斜率的收敛准则来确定。

(a)Mises应力分布

(b)变形图

图9δe/Di=1.5‰时分析模型的分叉屈曲模态(Pcr=1.003 MPa)

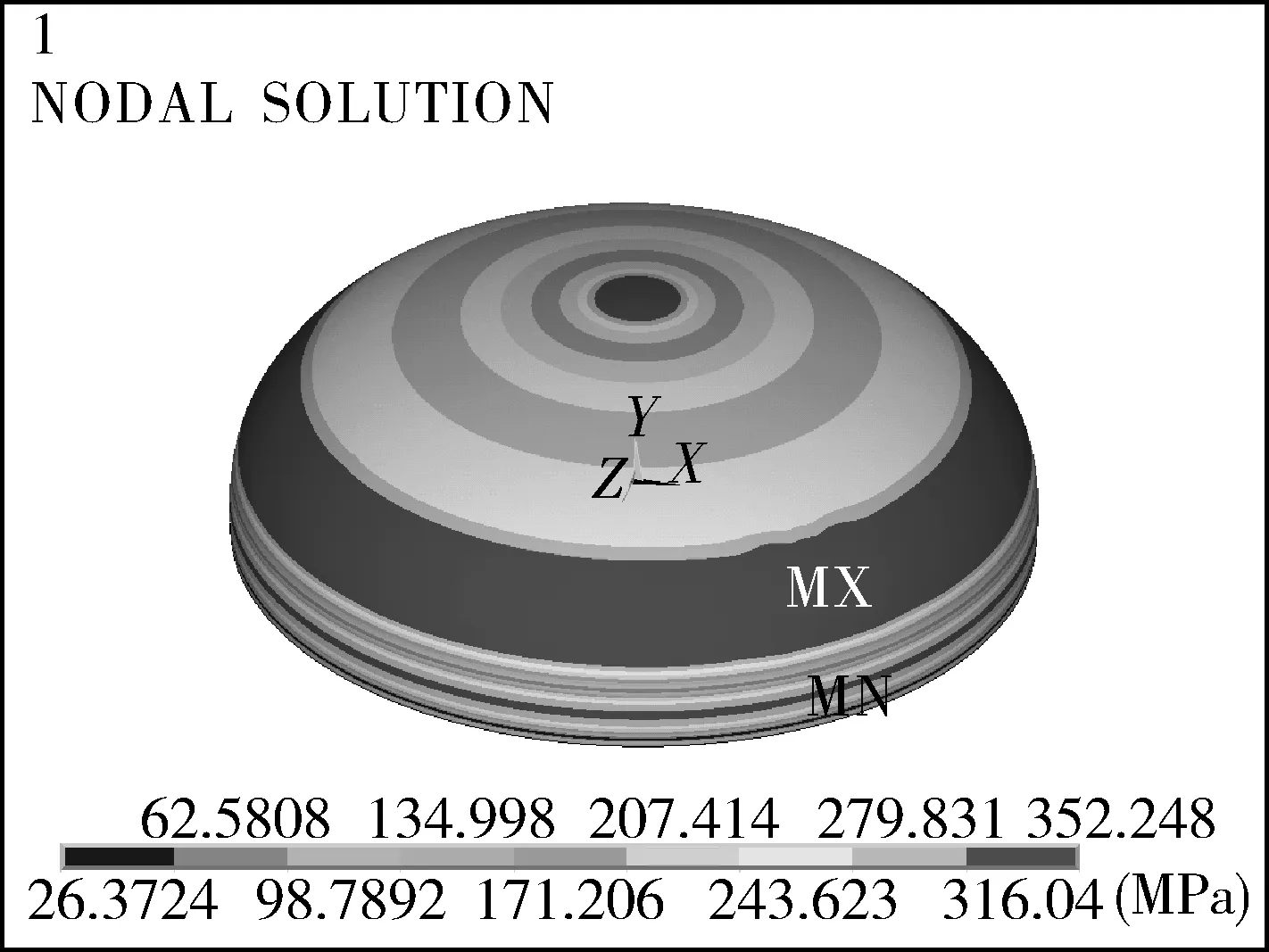
(a)Mises应力分布

(b)变形图

图10δe/Di=2.25‰时分析模型的分叉屈曲模态(Pcr=1.44 MPa)

仍以Q345R为例，对不同厚径比椭圆封头分析模型进行应力分析，对椭圆封头短轴端点最大拉应力处的载荷-位移曲线进行分析，计算所得极限载荷PL见表5。

表5 不同厚径比δe/Di分析模型极限载荷PL

图11示出了分析模型屈曲载荷Pcr和极限载荷PL与厚径比的变化关系。可以看出，对于Q345R标准椭圆封头模型，当厚径比δe/Di<1.649‰，屈曲载荷Pcr<极限载荷PL，此时椭圆封头分析模型的失效形式为周向屈曲；当厚径比δe/Di>1.649‰，屈曲载荷Pcr>极限载荷PL，此时容器的失效形式为强度破坏。

图11 椭圆封头模型屈曲载荷Pcr与极限载荷PL

4 常用其他材料屈曲分析失效载荷

4.1 不同厚径比δe/Di与不同材料下屈曲载荷Pcr

表6 不同厚径比δe/Di不同材料分析模型的屈曲载荷Pcr MPa

图12 分析模型屈曲载荷Pcr与厚径比δe/Di变化关系

表6列出了不同δe/Di、不同材料分析模型的屈曲载荷Pcr。可以看出，相同厚径比δe/Di下屈曲载荷Pcr随着材料屈服强度的增加而增加。图12示出不同材料分析模型屈曲载荷Pcr随δe/Di变化图。可以看出,各材料的屈曲载荷Pcr与厚径比δe/Di之间近似成正比关系。

4.2 极限载荷PL及屈曲载荷Pcr与δe/Di关系

采用第3.3节方法计算不同材料分析模型的极限载荷PL。表7列出各分析模型的极限载荷，图13示出不同材料椭圆封头分析模型屈曲载荷Pcr及极限载荷PL与厚径比δe/Di关系曲线。

表7 各材料椭圆封头分析模型的极限载荷PL MPa

(a)S31603

(b)S30408

(c)Q235B

(d)Q245R

(e)13MnNiMoR

由图13可以看出，各材料屈曲载荷与极限载荷随厚径比变化规律基本一致，随着厚径比增大，屈曲载荷与极限载荷显著增大；厚径比小于某临界值时，屈曲载荷低于极限载荷，分析模型发生屈曲破坏；厚径比大于某临界值时，屈曲载荷高于极限载荷，分析模型发生强度屈服破坏。各分析模型厚径比临界值见表8。

表8 各分析模型厚径比临界值

GB 150—2011对内压标准椭圆封头防止弹性屈曲的厚径比规定最小值为1.5‰，由表8可以看出，本文计算的防止屈曲失效厚径比值位于1.4‰～1.9‰范围内，多数材料模型得出的防止屈曲失效厚径比与标准规定(1.5‰)基本一致。但对于高强钢13MnNiMoR材料，本文计算得出的防止屈曲失效厚径比最小值为1.905‰，GB 150—2011的规定偏于冒进。本文结果可靠性尚需得到更多的试验支持。

5 结论

本文讨论了几种常用材料标准椭圆封头结构屈曲载荷Pcr与极限载荷PL的变化规律，得到主要结论如下。

(1)采用ANSYS软件中弧长法对某碟形封头进行非线性屈曲分析，对碟形封头局部过渡区引入15%厚度减薄量的单一缺陷,计算所得的分叉屈曲载荷0.597 MPa与前人试验值0.609 MPa基本一致，由此说明本文有限元内压屈曲分析解的可靠性。

(2)厚径比小于某临界值时，屈曲载荷低于极限载荷，分析模型发生屈曲破坏；厚径比大于某临界值时，屈曲载荷高于极限载荷，分析模型发生强度屈服破坏。不同材料标准椭圆封头分析模型厚径比临界值存在一定差异，但基本位于1.4‰～1.9‰范围内。

(3)GB 150—2011中规定：防止内压标准椭圆封头弹性屈曲失效的最小厚径比为1.5‰，对高强钢13MnNiMoR材料而言，这一规定偏于冒进。本文结果可靠性尚需得到更多的试验支持。