基于EEMD和单通道盲源分离的齿轮箱复合故障诊断研究

史云林，郝如江，安雪君

(石家庄铁道大学 机械工程学院，河北 石家庄 050043)

0 引言

齿轮箱的状态监测和故障诊断，对防止突发事故的发生和维持机械设备正常运行具有重大的意义［1］。在齿轮箱故障诊断研究中，大多是对齿轮箱的单一故障进行分析与诊断，目前对齿轮箱复合故障的研究较薄弱［2］。盲源分离(BSS)方法在机械设备故障诊断及状态监测中已获得成功应用。但是该方法大多局限于观测信号数目(传感器个数)需多于或等于源信号数目。实际情况中，由于成本问题，以及受监测环境所限，会出现仅能对其进行单通道监测的状况［3-4］。毋文峰等［5］将经验模态分解(EMD)与盲源分离结合用于机械故障诊断，实现单观测通道下机械振动信号盲分离。但是EMD分解存在模态混叠现象，而且在含有噪声的情况下效果不太好。李晓辉等［6］将总体经验模式分解(EEMD)和单通道盲源分离算法应用于轴承的单故障特征提取，但是对齿轮箱复合故障的提取还有待研究。针对以上问题，提出一种基于EEMD和单通道盲源分离的齿轮箱复合故障诊断算法，能有效提取齿轮箱的复合故障特征。

1 EEMD原理及IMF分量选择标准

1．1 EEMD原理

EEMD算法全称总体经验模式分解，为改进的EMD算法，不仅能有效抑制模态混叠现象，得到更有意义的IMF分量，而且能将原一维观测信号分解成多维，为实现信号的盲源分离创造条件［7］。EEMD算法步骤如下:

(1)将采集的信号x(t)中添加均值为零，标准差为常数的随机白噪声，得到含噪信号xi(t)，随机白噪声的标准差一般为采集信号标准差的0．1～0．2倍。

(2)对xi(t)进行EMD分解，得到K个IMF分量。

(3)重复进行步骤(1)和(2)各N次，每次添加的白噪声序列不相同。

(4)由于不相关随机白噪声序列的统计均值为零，对相应的IMF分量相加取均值，消除各个IMF分量的噪声成分，得到EEMD分解后的IMF分量。

式中，i=1，2，…，N;j=1，2，…，K。cj(t)为经EEMD分解得到的第j个IMF分量，N为添加白噪声的次数，一般情况下取50或100。

1．2 峭度标准

峭度K是归一化的四阶中心矩，作为一个无量纲参数，反映了振动信号的分布特性［8］，其定义为

式中，μ和σ分别为信号x的均值和方差，E(x－μ)4表示四阶数学期望值。

峭度特征与系统转速、尺寸、载荷无关，对冲击信号特别敏感。当齿轮箱的齿轮或轴承发生故障，引起机械冲击时，峭度值随之增大。峭度值的大小也从一个侧面反映了故障的严重程度［9-10］。

1．3 相关系数标准

相关系数用来测定变量之间的相关程度。假设两个变量X和Y，相关系数可以表示为

式中，Cov(X，Y)是两个变量X和Y的协方差;D(X)、D(Y)分别为变量X和Y的方差，相关系数的取值范围是［－1，1］。相关系数越大说明两个变量的线性相关程度越高。

2 盲源分离算法

盲源分离算法有很多，采用基于特征矩阵联合对角化(JADE)的盲源分离算法［11］。由多通道信号x(t)=［x1，x2，…，xN］构建的一系列四阶累积量矩阵近似对角化，以确定分离矩阵W，从而实现对独立信源s(t)=［s1，s2，…，sN］的合理估计y(t)=Wx(t)。在计算四阶累积量之前，必须先对混合信号进行预白化，即经过一个线性变换Q，使得混合信号的各分量互不相关，得到白化后的信号z(t)=Qx(t)。白化Λ(M)信号的四阶累积量矩阵为

此式说明，用V阵对矩阵Cz(M)作二次型处理可以得到对角矩阵。任意选择p个不同的N×N维矩阵Mp，计算各N×N维矩阵下的四阶累积量矩阵。最后将这些累积量矩阵组合成一个大的矩阵Cz(Mp)，然后采用联合近似对角化方法对Cz(Mp)进行对角化，得到正交分离矩阵U。综上所述可以得到分离矩阵，W=UTQ。JADE算法步骤简要归纳如下［12］:

(1)对多通道信号x(t)中心化，并作白化处理，得到z(t)=Qx(t)。

(2)联合近似对角化z(t)的四阶累积量矩阵Cz(Mp)，得到酋矩阵U。

(3)计算分离矩阵W=UTQ。

(4)求得源信号s(t)的估计y(t)。

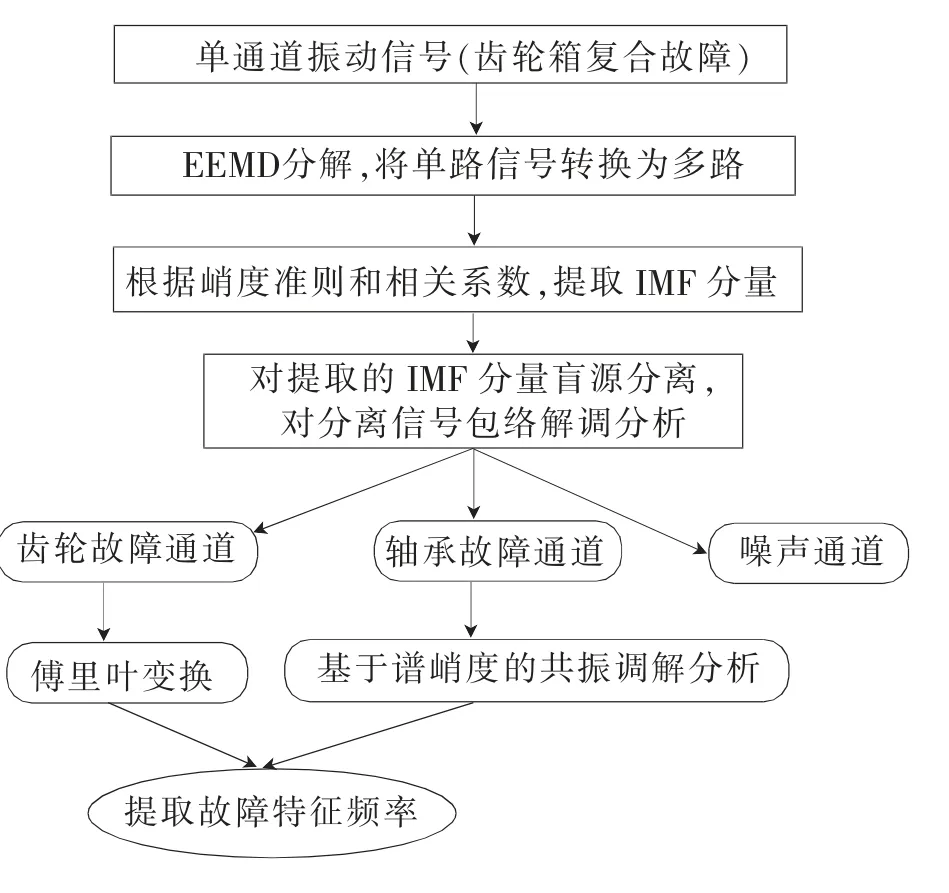
图1 齿轮箱复合故障诊断流程图

3 齿轮箱复合故障诊断流程

齿轮箱的复合故障为齿轮故障和轴承故障的复合，其中还有噪声干扰。基于本文算法，齿轮箱复合故障诊断的流程如图1所示。

4 实验验证

为验证所提方法的可行性及有效性，在齿轮箱实验台上进行了实验验证。实验台为美国DDS实验台，如图2所示，实验台从左至右依次为电动机，行星齿轮箱，定轴齿轮箱，磁粉制动器。其中齿轮传动简图如图3所示。

图2 齿轮箱实验台

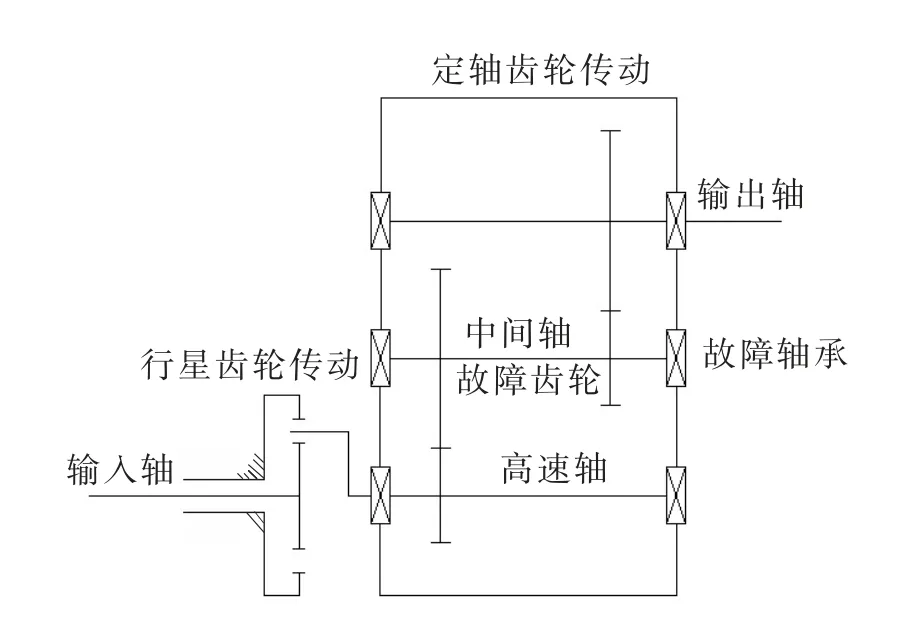
图3 齿轮传动简图

齿轮传动为三级传动，各级传动齿轮齿数及传动比如表1所示。

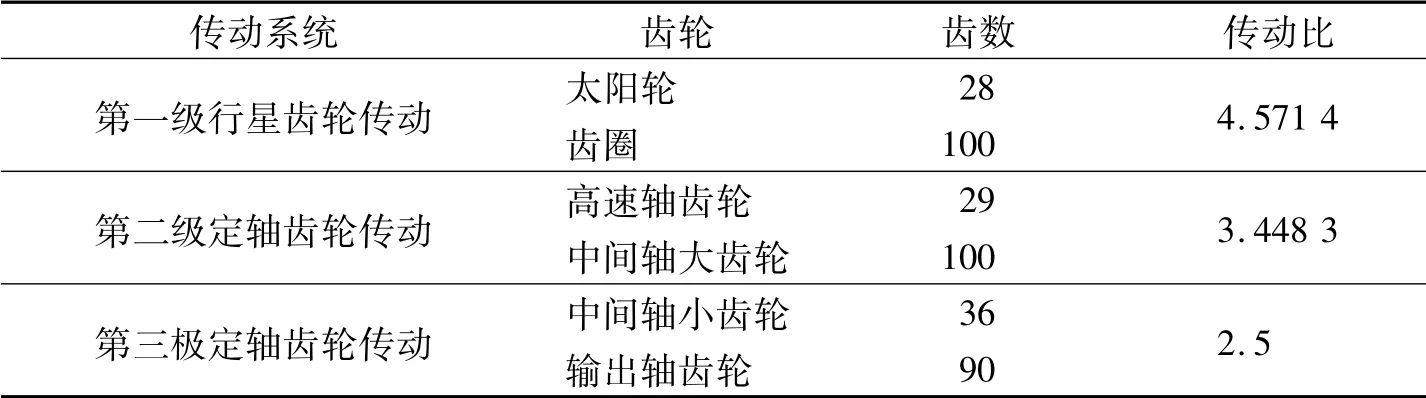
表1 各级传动齿轮齿数及传动比

齿轮箱故障采用齿轮缺齿和轴承内圈故障的复合，故障设置在中间轴上，可参见图3。其中轴承型号为ER16K，轴承的几何参数如表2所示。在轴承内圈加工点蚀故障，点蚀的直径为1 mm，深0．5 mm。

表2 轴承的几何参数

用单个加速度传感器采集齿轮箱振动信号，传感器布置在故障轴承轴承座的上方。

设定实验台电动机转速为2 400 r/min，负载调节磁粉制动器显示为1．8 A，计算传动系统中的轴的转频、齿轮啮合频率、轴承内圈故障频率如表3所示。

表3 传动系统中相关频率 Hz

用DASP振动信号采集仪采集振动信号，采样频率为25 600 Hz，采样时间为10 s，取前2 s数据进行分析。得到的故障齿轮箱时域波形如图4所示，对信号进行包络后的频谱如图5所示。在相同条件下，测得正常齿轮箱信号时域图如图6所示，对信号进行包络后的频谱如图7所示。

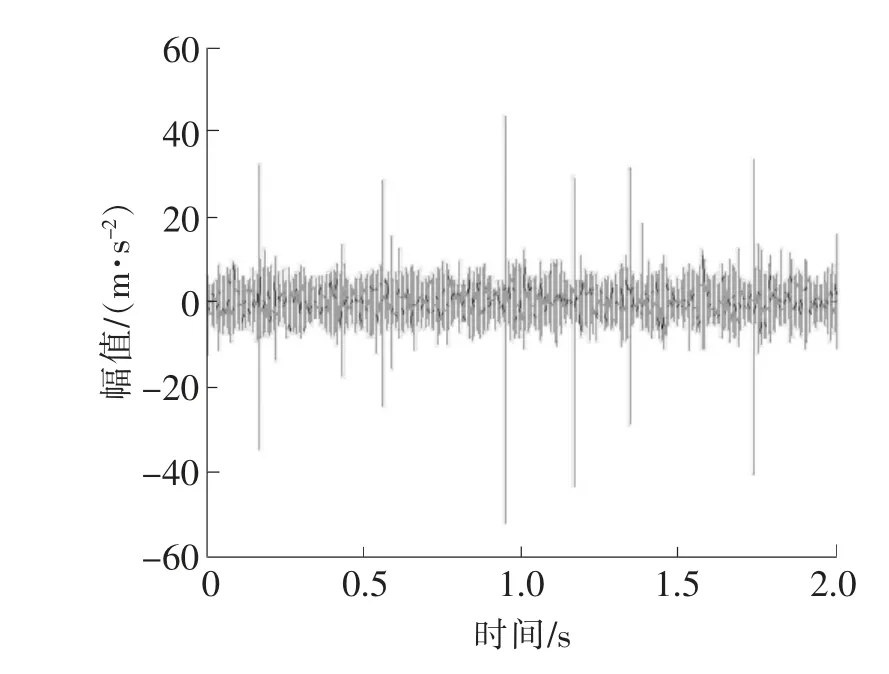
图4 故障信号时域图

图5 故障信号包络频谱图

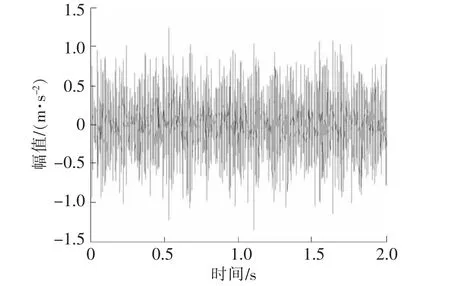
图6 正常信号时域图

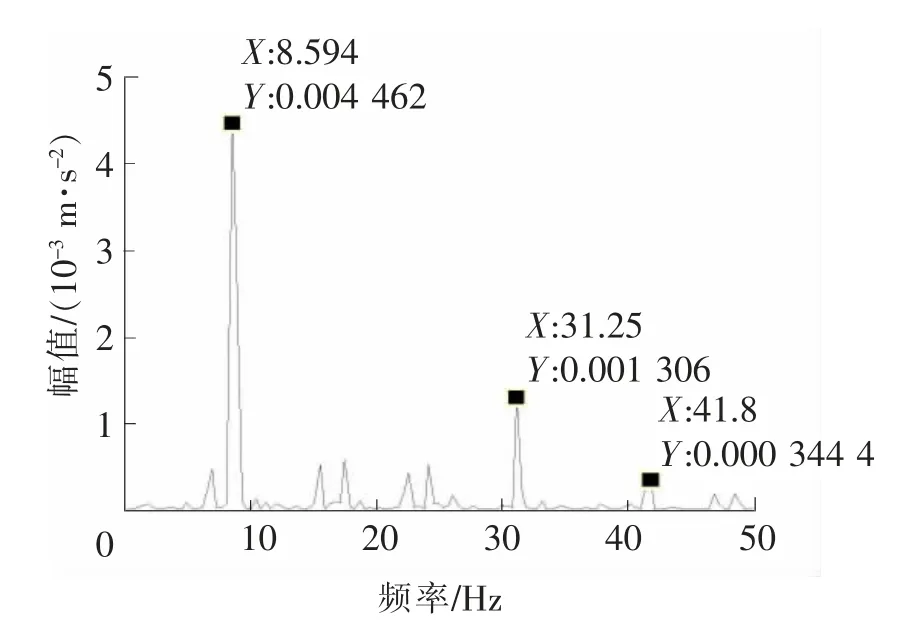
图7 正常信号包络频谱图

通过图4和图6的对比，可知从图4中可以看到信号有明显的冲击成分，初步分析传动系统中某一齿轮存在断齿故障。图5中含有高速轴转频8．984 Hz(理论值8．75 Hz)，输入轴的转频40．63 Hz(理论值40 Hz)，其中17．58 Hz为高速轴的二倍频。图7中也含有高速轴转频8．594 Hz(理论值8．75 Hz)，输入轴的转频41．8 Hz(理论值40 Hz)，两者的差为31．25 Hz。通过图5和图7的对比可知，在故障信号和正常信号中，高速轴转频和输入轴转频的幅值都很高，它们为故障信号中的主要噪声干扰。故障特征被噪声湮没，难以辨别。对故障信号进行EEMD分解得到8个IMF分量，如图8所示。

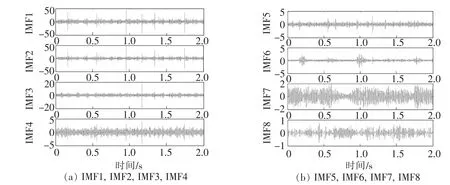
图8 EEMD分解IMF时域图

计算各IMF分量的峭度值，各分量和故障信号的相关系数如表4所示。

从表4中可得前3个IMF分量和第6个IMF分量的峭度值较大，前3个IMF分量和故障信号的相关系数较大，综合峭度和相关系数计算结果，选择IMF1、IMF2、IMF3这3个信号进行盲源分离。对盲源分离后重构的信号进行包络谱分析，得到包络后的频谱如图9所示。

表4 各IMF分量选择标准计算结果

图9中第一通道主要频率为高速轴转频8．984 Hz(理论值8．75 Hz)，为噪声通道。第二通道中可以看到轴承内圈故障频率13．67 Hz(理论值13．779 Hz)，为轴承故障通道。同时也有高速轴转频8．594 Hz及其二倍频17．58 Hz的干扰。第三通道中，可以看到中间轴转频2．344 Hz(理论值2．537 5 Hz)及其二倍频5．078 Hz，为齿轮故障通道，可以判断中间轴上某一齿轮存在断齿故障。同时可以看到40．63 Hz约为输入轴转频(理论值40 Hz)，为噪声干扰。为了进一步确定中间轴上哪一个齿轮存在故障，对第三通道做频谱分析，如图10所示。

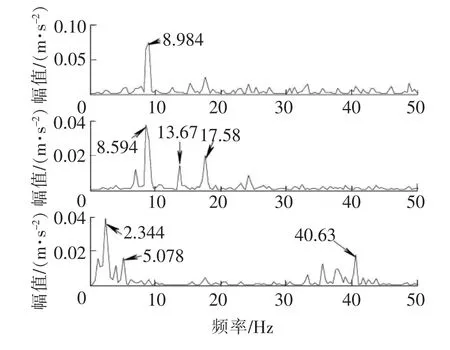
图9 盲源分离后的包络频谱图

图10 第三通道频域图

从图10中可以看到，第三级定轴齿轮传动的啮合频率91．41 Hz(91．35 Hz)，并且可以找到它的二倍频183．2 Hz、三倍频274．6 Hz。由此可以判断中间轴上的小齿轮发生断齿故障。从频域图中还可以看到40．63 Hz为输入轴转频，129．7 Hz和132 Hz为第三级啮合频率91．41 Hz和输入轴转频40．63 Hz的累加频率，被中间轴转频2．344 Hz调制而成，253．9 Hz为第二级啮合频率(253．75 Hz)，这些为干扰噪声。

为了进一步确定轴承故障，对第二通道做基于谱峭度的共振解调分析。第二通道的谱峭度图如图11所示，谱峭度值最大时所对应的中心频率fc=8 000 Hz，带宽Bw=1 066．67 Hz。用该共振带参数设置切比雪夫带通滤波器，滤波以后结合Hilbert变换对该通道振动信号包络频谱分析。包络之后的频谱如图12所示。从图12中可以看到轴承内圈的故障频率13．67 Hz(理论值13．779 Hz)，及其二倍频27．34 Hz，三倍频41．02 Hz。还可以看到围绕内圈通过频率及其谐波，间距为中间轴转频2．74 Hz(理论值2．537 5 Hz)的调制边带。由此可以判断中间轴上轴承内圈发生故障。

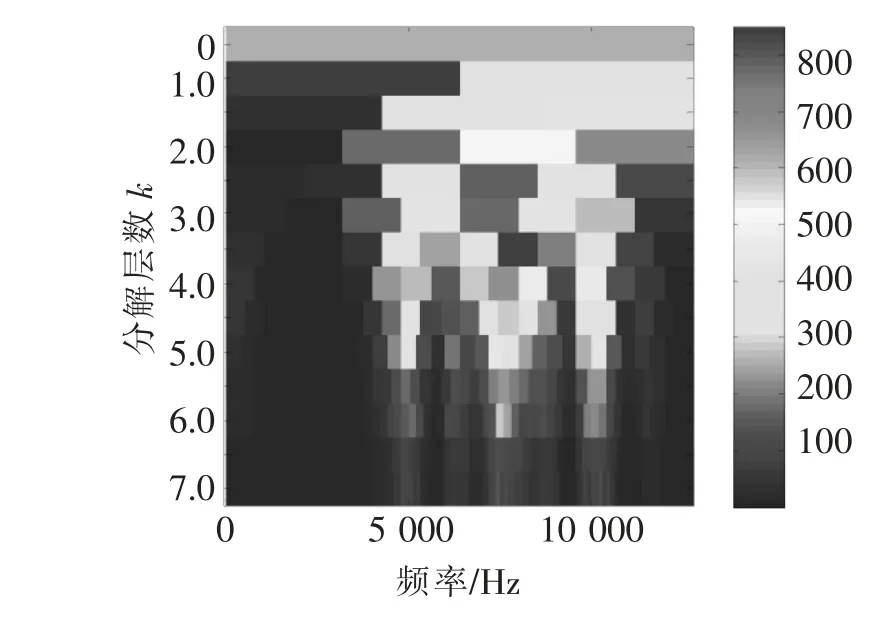
图11 第二通道谱峭度图

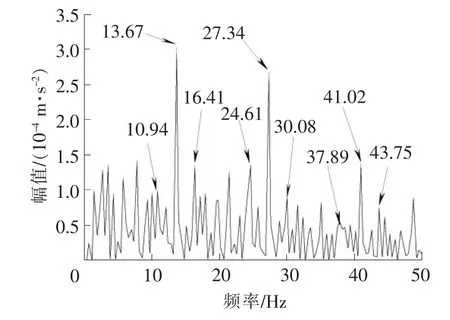
图12 带通滤波后的包络频谱图

5 结论

研究表明，基于EEMD和单通道盲源分离的齿轮箱复合故障诊断方法，在使用单个加速度传感器和含有噪声干扰的条件下，可以实现对齿轮和轴承复合故障特征的分离以及提取。其中EEMD分解后，通过峭度和相关系数能有效地提取IMF分量，盲源分离将不同故障类型和噪声分离开，结合谱峭度图和共振解调技术提取轴承微弱故障，通过实验验证了该方法的有效性。