移动荷载作用下曲线桥的动力响应分析

李皓玉，宋 健，任剑莹

(1．石家庄铁道大学 工程力学系，河北 石家庄 050043 2．石家庄铁道大学 交通环境与安全工程研究所，河北 石家庄 050043)

0 引言

随着我国交通运输的快速发展，交通量越来越大，曲线桥由于能较好地适应桥址受地形和路线限制的需要，可以更好地改善交通枢纽的美观程度，因此，曲线桥在我国的高等级公路建设以及城市道路的互通立交桥梁中得到了很大的发展与进步［1-2］。

车辆与桥梁的动力相互作用是一个复杂的课题，国外很多学者对其进行了研究，并取得了重要成果［3-5］。李华等［6］基于纯扭转理论单根曲线梁法，对常见的约束扭转简支支座等截面连续曲线梁进行了分析。宋郁民等［7］以新建的某铁路货运专线上的反向曲线上的小半径曲线桥梁为例，考虑列车曲线通过的特点及轮轨非线性相互作用，得出列车通过该反向曲线上小半径曲线梁桥的一些振动规律。单德山等［8］以某铁路曲线连续梁桥方案为例，讨论了大跨度铁路曲线梁桥的车桥耦合振动。郭秀英等［9］采用GSB方法研究车桥耦合模型一些特殊情况下的近似解。但这主要集中在了曲线桥理论计算以及铁路曲线桥的研究，因此研究公路曲线桥在移动荷载作用下的动力响应是很有必要的，而且曲线桥在使用过程中，上部结构容易发生横桥向的变位，但很少有学者进行这方面的研究，因此考虑曲线桥的横向位移也是很重要的。

1 曲线梁的有限元模型及数学模型

1．1 依托工程简介

图1为江西某等截面单箱双室钢筋混凝土曲线连续箱梁桥示意图。图1(a)为该曲线桥横截面示意图，箱梁顶板平均厚度为0．28 m、底板平均厚度为0．25 m，腹板平均厚度为0．65 mm。箱梁顶板横向宽12 m，箱底宽8 m，翼缘悬臂长2 m。图1(b)为该曲线桥立面示意图，纵向坡度为7%，跨径为15 m+15 m+15 m+17 m、平均曲率半径50 m。钢筋混凝土材料的弹性模量E=3.3×1010N/m2，密度ρ=2 600 kg/m3，泊松比μ=0.2。

为便于叙述，文中定义该曲线桥孔跨从左向右依次为第一跨，第二跨，第三跨，第四跨，桥墩从左到右依次为0，1，2，3，4号。

图1 曲线箱梁横截面及其立面示意图(单位:cm)

1．2 有限元模型建立

利用有限元软件ANSYS，采用solid45单元，建立了该曲线桥的有限元实体模型，如图2所示。该模型共包含16 532个单元，23 779个节点。曲线桥桥端采用固定支座，其它支座采用活动支座。将车辆简化为不考虑质量惯性的匀速移动的竖向集中荷载，将车辆离心力简化为匀速移动的横向集中荷载。选取桥面正中间沿桥向的节点作为荷载移动的位置轨迹对第一个节点施加竖向和横向荷载，当该荷载移动到下一节点时，将之前节点上的荷载删除，以此来实现车辆在曲线桥上的移动，计算移动荷载作用下曲线桥的动力响应。

图2 曲线桥有限元模型

1．3 曲线梁在移动荷载作用下的数学模型

对于图3所示多跨曲线梁，在移动速度为v的荷载(竖向力P0、扭矩T0)作用下，其动力响应的控制微分方程是

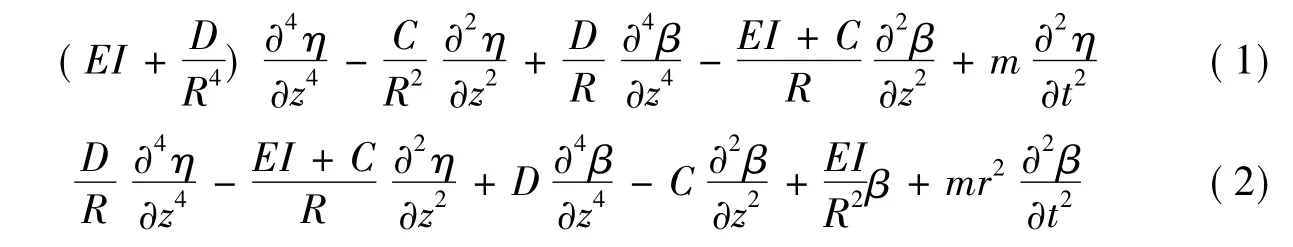
式中，η为竖向位移，η=η(z，t);β为扭转角，β=β(z，t);EI是曲线梁的抗弯刚度;C=GJ是截面的翘曲刚度，J是圣维南扭转常数;D=EIω是截面的翘曲刚度，Iw是翘曲系数，对于箱形、圆形薄壁闭口截面为零，对于工字形、槽形等开口截面为非零值;m是单位长度的质量;是截面的回转半径，Ip是截面对于z轴的二次矩，A是截面面积。

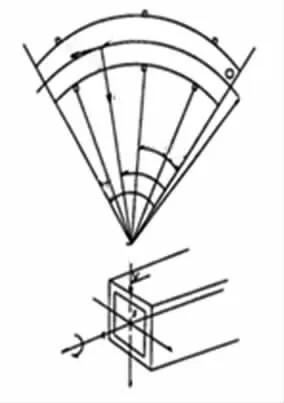
图3 多跨曲线梁的平、剖面图

2 有限元模型验证

2016年，在该曲线梁桥上进行了现场试验。试验采用电磁式测试系统，利用脉动法进行自振频率测试，由加速度传感器作拾振器，经电荷放大，然后进行信号处理，通过对脉动波形进行谱分析，得到脉动时桥梁的自振频率，同时利用ANSYS对现场试验工况进行了模拟，并将有限元计算值与试验数据进行了对比。曲线桥竖向一阶和二阶频率的实测值和有限元计算值见表1。重42 t的车辆分别以5，10，15 km/h不同速度行驶在曲线桥上时，第三跨跨中挠度的实测值和有限元计算值见表2，1，2，3号桥墩墩顶横向位移的实测值和有限元计算值见表3。

表1 频率实测值和有限元计算值

表2 挠度实测值和有限元计算值

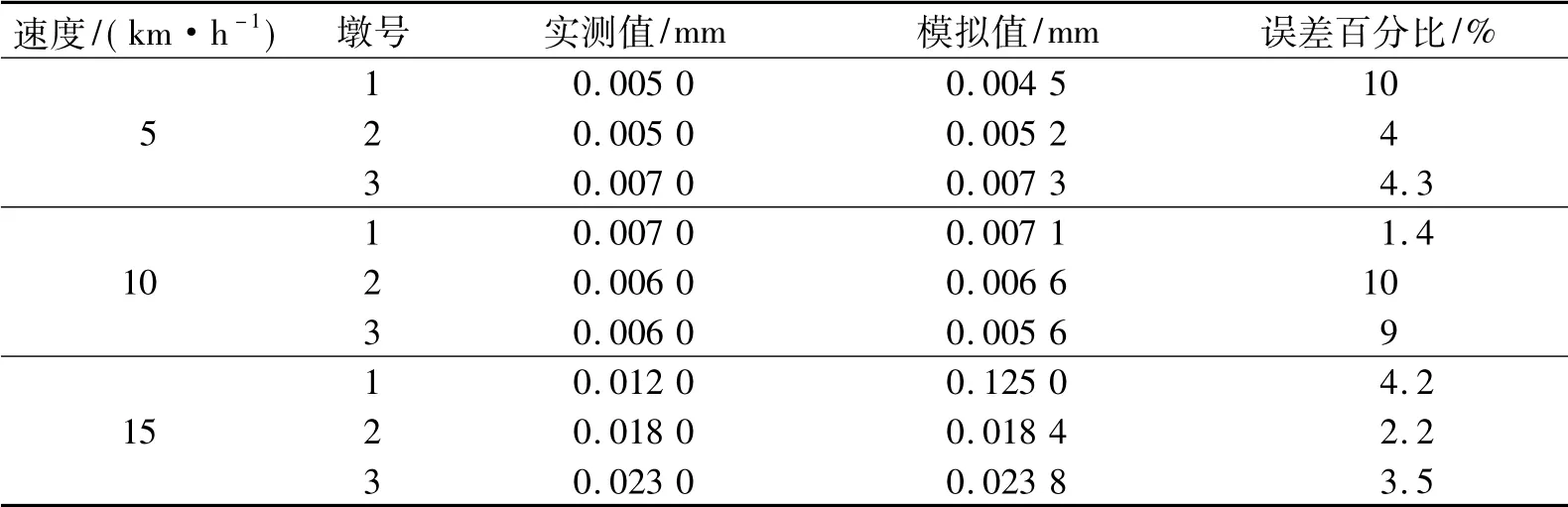
表3 墩顶横向位移实测值和有限元计算值

根据有限元计算值和现场试验数据的对比可以发现，曲线桥一阶频率相差3．1%，二阶频率相差8.3%，不同速度下，第三跨跨中挠度最大相差10．6%，墩顶横向位移最大相差10%，误差是在允许范围内的。误差存在的主要原因是该有限元模型的约束不能完全与实际曲线桥的约束一致，以及移动荷载不能完全模拟实际车辆行驶在曲线桥上的情况。所以该有限元模型还是可以较好地模拟该曲线桥。

3 不同参数下曲线桥的动力响应

依据上述有限元模型，计算了移动荷载作用下曲线桥跨中位移、扭转角和始端支座反力等的动力响应，讨论了车辆离心力，车辆载重以及车速对曲线桥动力响应的影响，由于篇幅有限，只分析了各参数对曲线桥第三跨跨中位移和扭转角以及曲线桥始端支座反力的影响。

3．1 离心力对曲线桥动力响应的影响

车辆通过曲线桥时，会有离心力的存在，离心力的表达式F=mv2/r，其中，m代表质量;v代表速度;r代表离心运动半径。本节分析了车辆载重25 t，以10 m/s的速度通过曲线桥时，车辆离心力对曲线桥第三跨跨中竖向位移、横向位移、扭转角以及支座反力的影响，结果如图4所示。

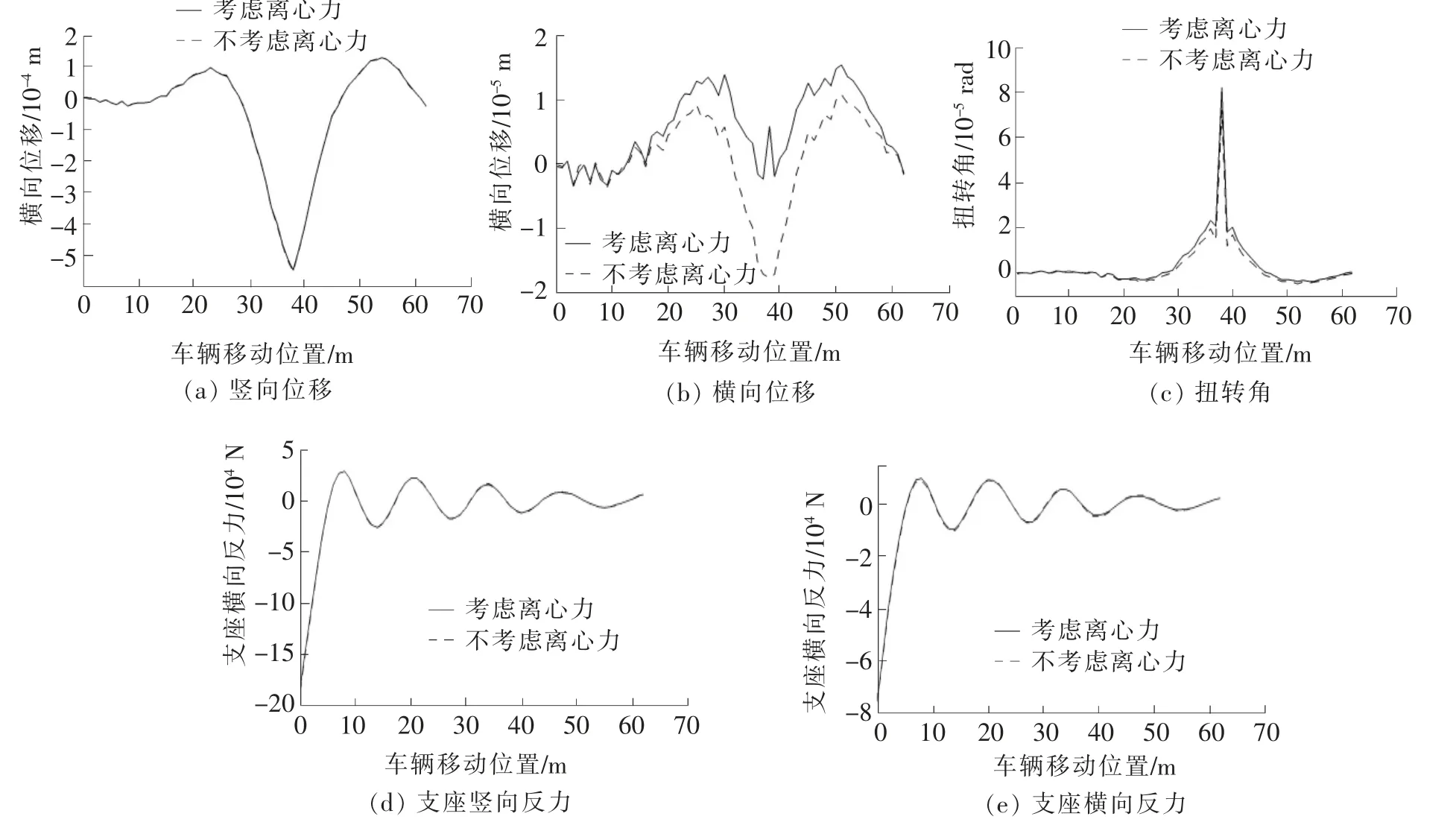
图4 离心力对曲线桥动力响应的影响

由图4可以看出:(1)离心力对曲线桥竖向位移和支座反力影响不大(图中两条曲线基本重合);(2)不考虑离心力时，车辆在驶入和驶离第三跨时，第三跨跨中存在较大的朝向曲线桥外侧的横向位移，车辆位于第三跨跨中时，第三跨跨中存在较大的朝向曲线桥内侧的横向位移，考虑离心力时，朝向外侧的横向位移会变大，而朝向内侧的横向位移会变小，说明离心力使曲线桥产生朝向外侧的横向位移;(3)离心力会增大跨中扭转角，不考虑离心力时，第三跨跨中最大扭转角为7.2×10－5rad，考虑离心力时，最大扭转角为8.1×10－5rad，变化幅度约为12．5%，与文献［10］得到的结论一致。

3．2 车辆载重对曲线桥动力响应的影响

分析了车辆在不同载重情况下(15 t，25 t，35 t，45 t)，以10 m/s的速度通过曲线桥时，曲线桥第三跨跨中竖向位移、横向位移、扭转角以及支座反力的动力响应，结果如图5所示。

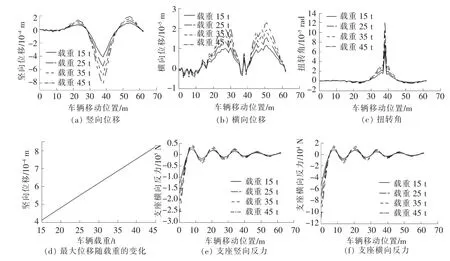
图5 车辆载重对曲线桥动力响应的影响

由图5可以看出:(1)曲线桥跨中竖向位移、横向位移、扭转角以及支座反力均随车辆载重的增加呈线性增长，由于篇幅有限，图5只给出了竖向位移随载重的变化趋势;(2)随着载重的增加，车辆产生的离心力也会增大，在载重和离心力的共同影响下，朝向曲线桥外侧的横向位移随着载重的增大而变大，但朝向曲线桥内侧的横向位移并没有随着载重的增加而变小(离心力产生的朝向外侧的横向位移会抵消朝向内侧的横向位移)，说明车辆产生的竖向荷载对曲线桥动力响应的影响大于横向荷载(离心力)对曲线桥动力响应的影响。

3．3 车速对曲线桥动力响应的影响

分析了车辆载重25 t，分别以5，10，15，20 m/s的速度通过曲线桥时，曲线桥第三跨跨中竖向位移、横向位移、扭转角以及支座反力的动力响应和各响应最大值的变化趋势，结果如图6所示。

由图6可以看出:(1)曲线桥跨中竖向位移随车速的增加先变大后减小，当车速在7 m/s时，跨中竖向位移有最大值，可能是由于车辆对桥梁的加载频率与该曲线桥本身的固有频率接近而造成桥梁振幅增大［11］;(2)曲线桥跨中横向位移和扭转角随着车速的增加而增大，当车速较低时，曲线桥跨中产生朝向曲线桥内侧的横向位移，随着车速的增大，跨中产生朝向曲线桥外侧的横向位移;(3)随着车速的增加，支座反力在减小。说明车速较快时，车辆通过曲线桥的时间较短，曲线桥振动还没有来得及充分发展，车辆己经驶过。

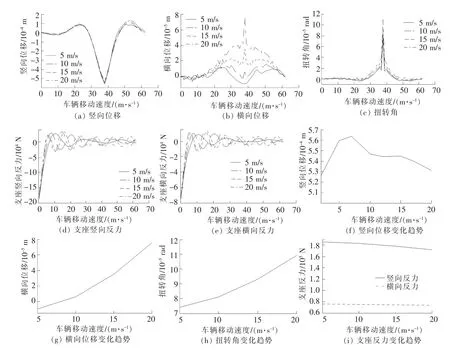
图6 车速对曲线桥动力响应的影响以及响应最大值随车速的变化趋势

4 结论

(1)离心力会使曲线桥产生朝向曲线桥外侧的横向位移，离心力对曲线桥竖向位移和桥端支座反力影响很小，但对曲线桥扭转角的影响较大，最大变化幅度约为12．7%。

(2)曲线桥跨中竖向位移、横向位移、扭转角以及支座反力随着载重的增加呈线性增长。

(3)竖向荷载对曲线桥动力响应的影响大于横向荷载对曲线桥动力响应的影响。

(4)随着车速的增加，曲线桥跨中横向位移逐渐增大;支座反力逐渐减小;竖向位移先变大后减小，在7 m/s时有最大值，可能是由于此时车辆对桥梁的加载频率与该曲线桥本身的固有频率接近而造成桥梁振幅增大。