基于高阶剪切变形理论梁的热屈曲和后屈曲分析

于旭光，申幸幸，郑 宏

(1．唐山工业职业技术学院 建筑化工系，河北 唐山 063299;2．长安大学 建筑工程学院，陕西 西安 710061)

0 引言

梁、板、壳体是工程中最常用的结构构件，它们在热荷载或轴向荷载作用下的屈曲分析问题长期受到国内外学者的密切关注。尽管对于各向同性及层合梁结构的非线性问题研究已经十分丰富［1-3］，但是对于该领域的研究却一直没有间断。国外学者Aydogdu［4］分析了基于Reddy位移模型下层合梁在各种边界条件下的热屈曲分析。Kiani et al［5］分析了功能梯度材料梁的热屈曲问题。Emam［6-7］分析了层合梁在湿热环境中的屈曲和后屈曲问题。马连生等［8-9］给出了经典梁及剪切变形梁的热过屈曲问题的解析解，但未采用高阶剪切变形理论来对梁的屈曲和后屈曲问题进行分析。

1 模型

考虑一个高度为h、宽度为b、长度为l的矩形截面梁:x轴沿梁轴线方向;z轴和y轴分别沿梁的厚度和宽度方向;xoy面置于梁的几何中面上;原点位于梁轴线的左端［8］。

1．1 位移场

文献［10］给出了高阶剪切变形理论下的位移场为

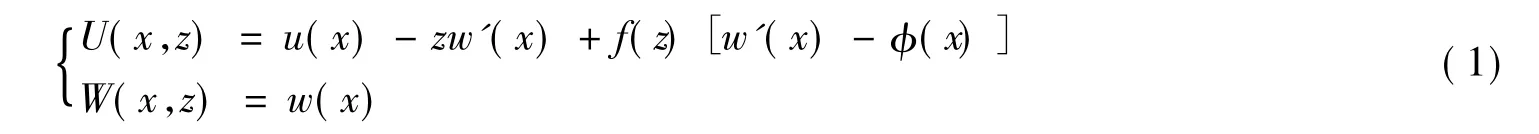
式中，u和w分别为梁中面上点的轴向和横向位移;为梁中面上横截面由于弯曲产生的转角;f(z)为形状函数，表达式见表1。

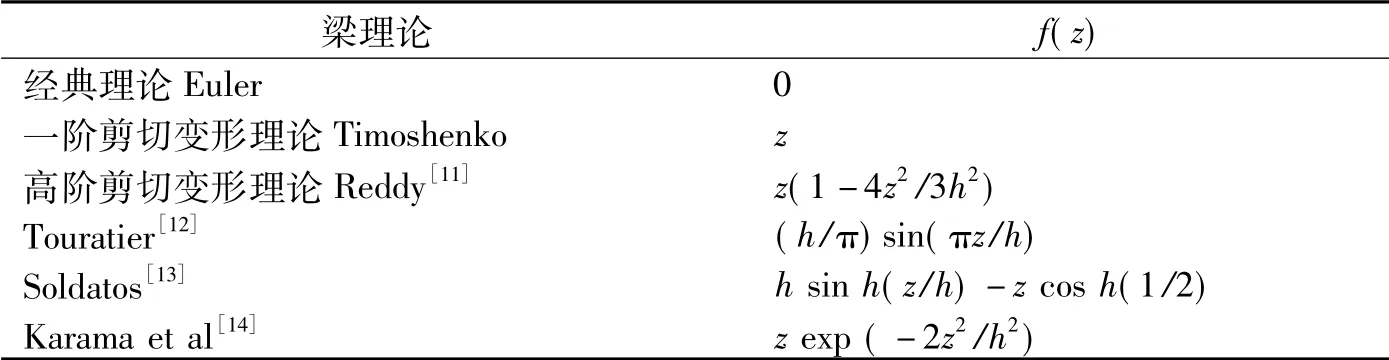
表1 不同梁理论的剪切应变形状函数

1．2 应变场

基于上述位移场的正应变和剪应变为

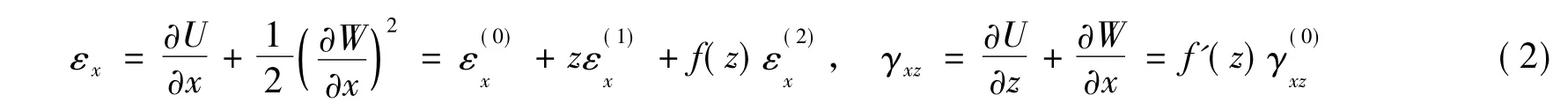
1．3 应力应变关系

考虑温度的变化，梁的应力应变关系可以表达如下

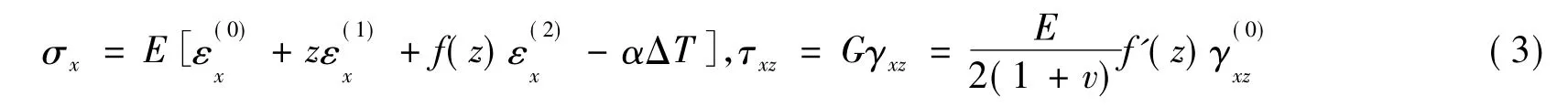
式中，E为弹性模量;G为剪切模量;v为泊松比;α为热膨胀系数;ΔT为温度改变量。现令

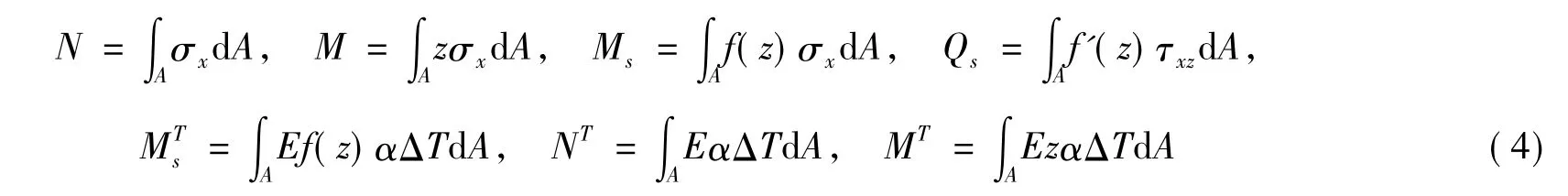
式中，N和M为经典理论下的轴力和弯矩;Ms和Qs为由于剪切变形产生的弯矩和剪力;NT、MT和MTs为热内力和热弯矩，它们是由于温度变化所引起。

将式(3)代入式(4)中可得到上述合力与应变的关系可以表达为

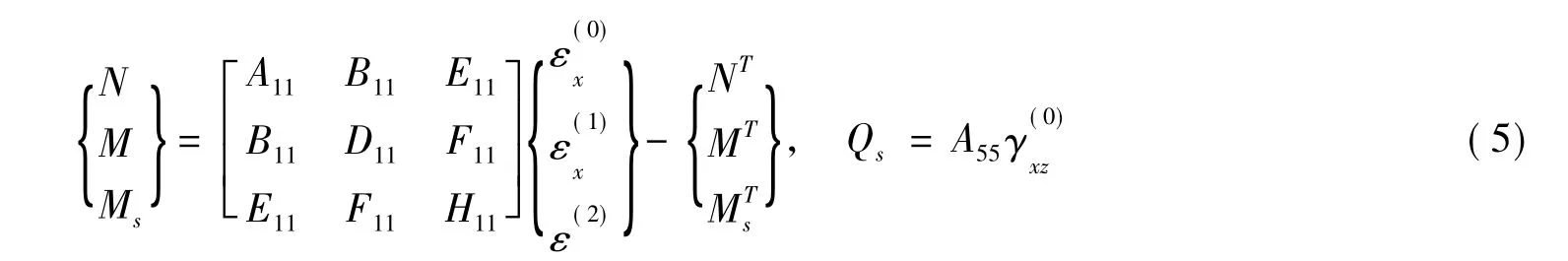
2 平衡方程及求解

根据最小势能原理，总势能的一阶变分为0，即δ∏=0，由此可得梁的平衡方程为

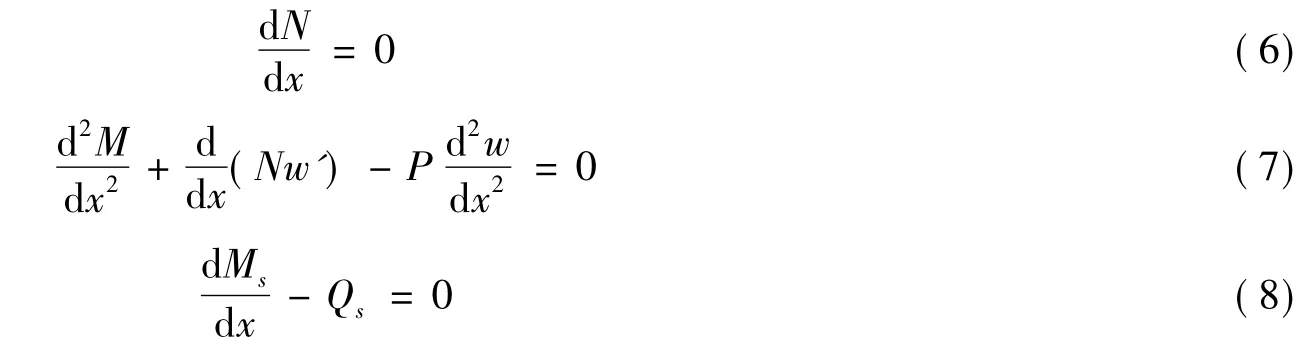
边界条件为:

固支端

简支端

将式(5)代入式(6)、式(7)、式(8)可得到

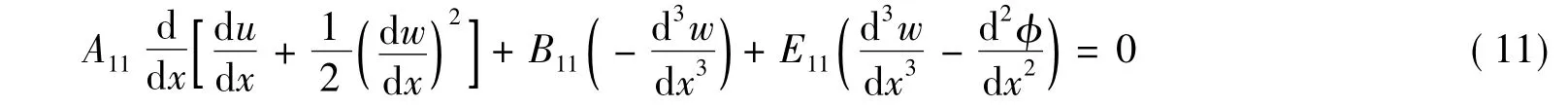
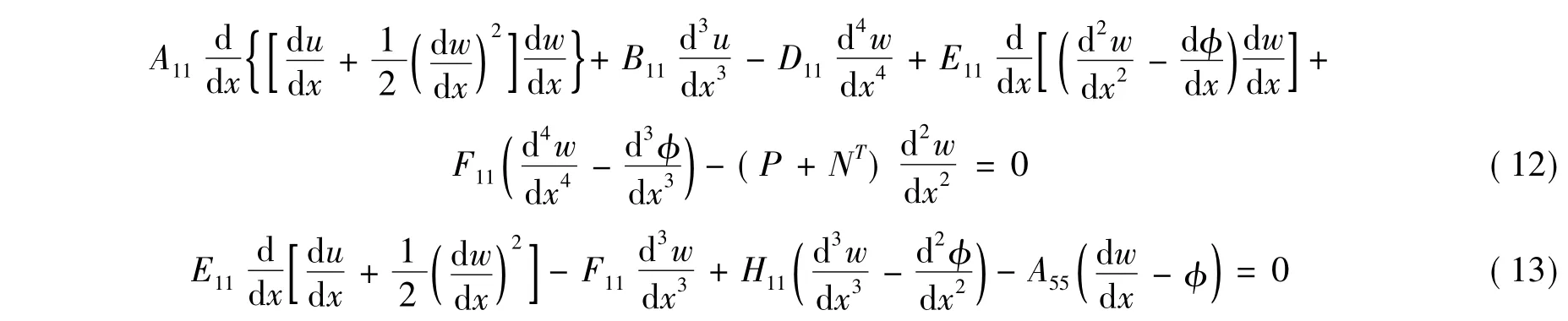
将式(11)对x积分一次得到

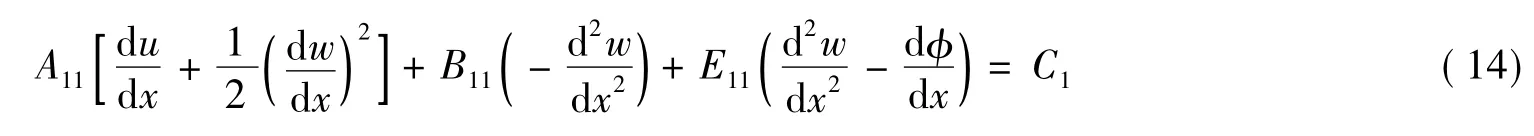
从式(14)可得出

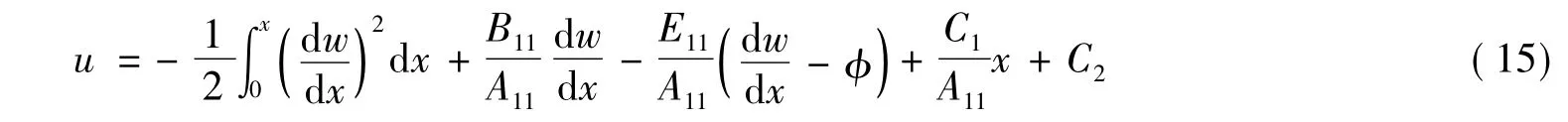
根据式(5)中知B11=E11=0，由固支端和简支端的边界条件u(0)=u(l)=0，得到

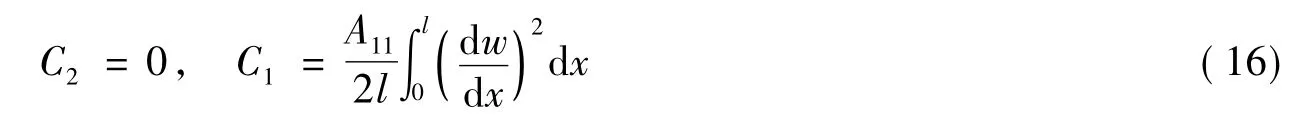
将式(16)代入式(14)得到

对式(17)两边对x求导一次得到

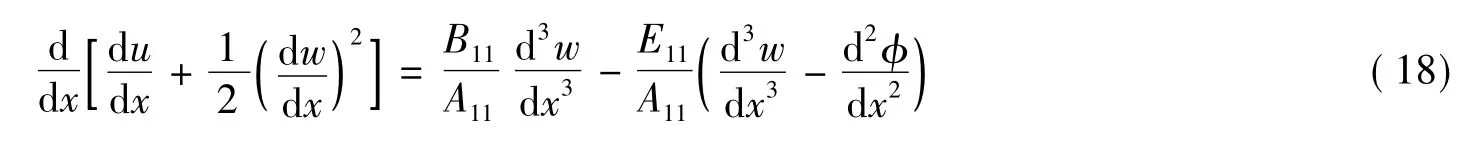
对式(18)两边再对x求导一次整理后得到

将式(17)、式(18)、式(19)代入式(7)、式(8)得到

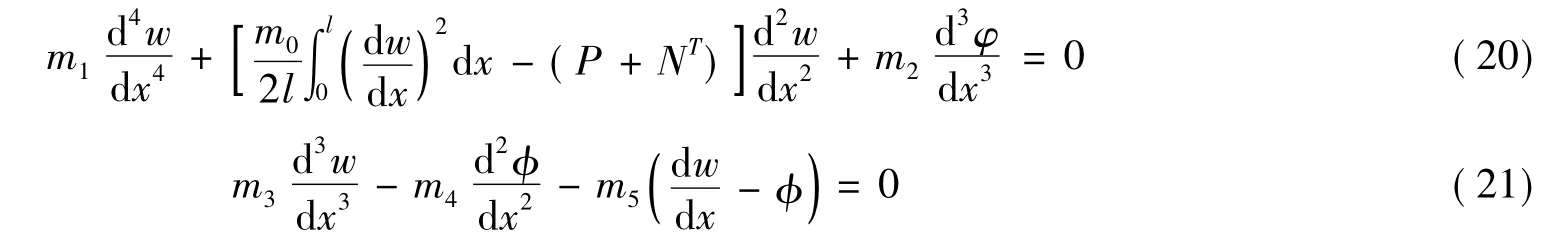
式(20)、式(21)便是关于横向挠度和转角的非线性积分—微分方程。

对于两端简支梁:

根据式(5)中可知B11=E11=0，由式(5)得到

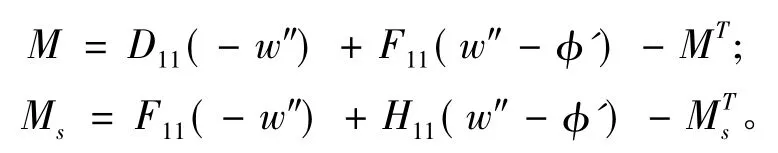
由式(5)中可知D11，F11，H11都不为0，由式(10)给出的两端简支梁的边界条件

目标要求：理解诚实正直三原则及其重要性；学习重要词汇和习惯表达法；把握文章各部分的重要信息；分析文章结构和逻辑组织方法，完成相关词汇、语法和翻译练习。

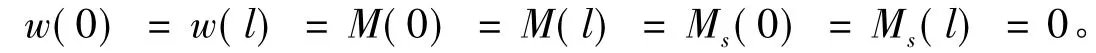
可以将两端简支梁的边界条件可以转化为

由文献［15］知，第一阶屈曲模态是结构唯一稳定的平衡位置。假设两端简支梁下的位移函数为

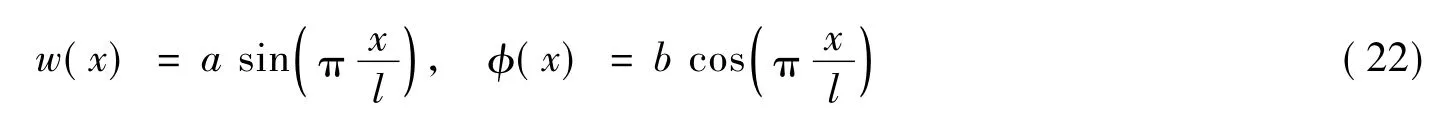
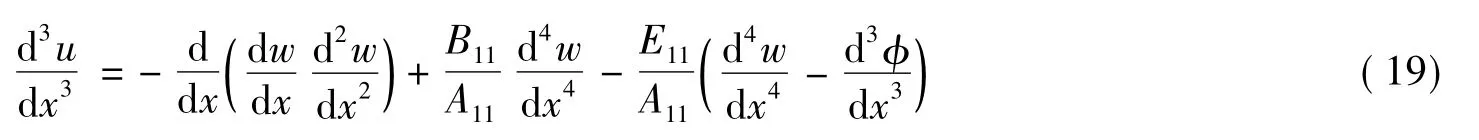
将式(22)代入式(20)、式(21)可以得到如下的表达式

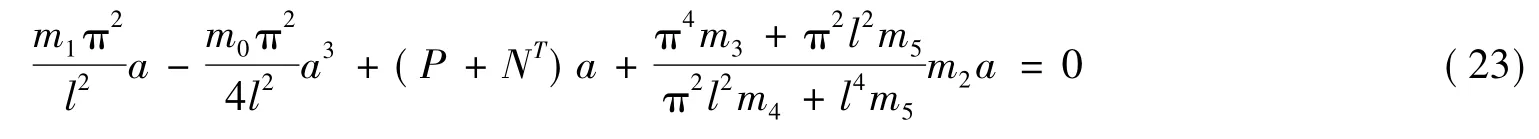
可以看出，式(23)有3个解，第一解:a=0反映梁前屈曲的直线平衡状态;剩下两个解:a≠0，反映梁后屈曲的稳定平衡位置状态。可以求出梁的后屈曲幅值(即跨中挠度)为

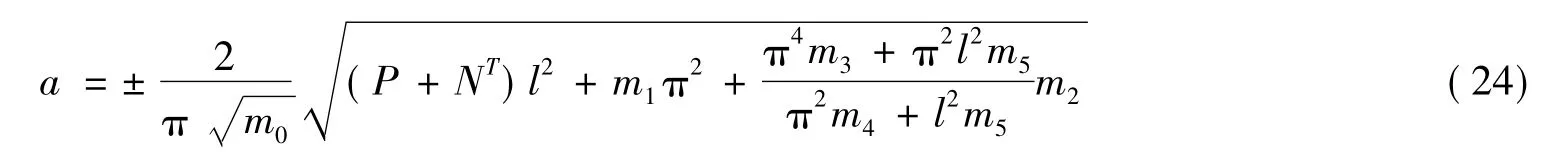
舍去式(23)中非线性项也可以得到临界屈曲荷载为

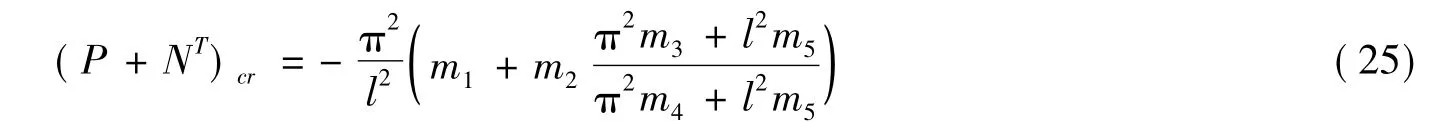
对于两端固支梁:

由边界条件w(0)=w(l)=w'(0)=w'(l)=(0)=(l)=0，假设两端固支梁下的位移函数为

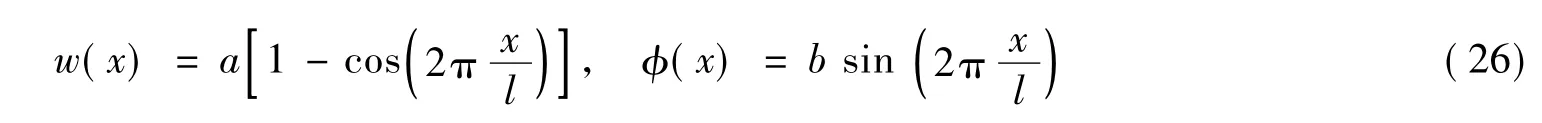
同样可以求出后屈曲幅值(即跨中挠度)为

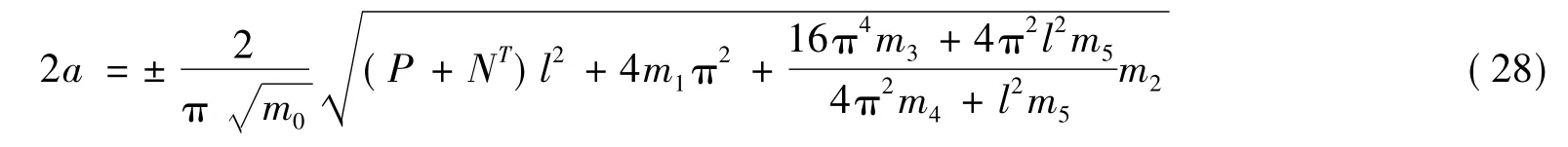
舍去非线性项可以得到临界屈曲荷载为

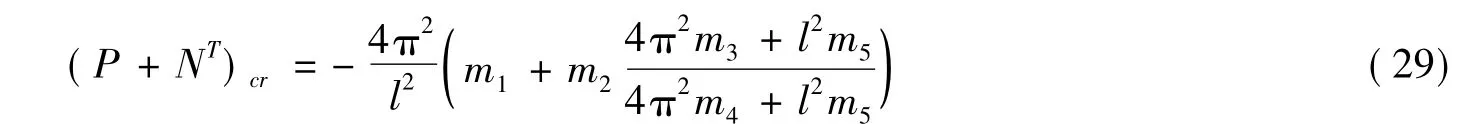
对应于经典的欧拉梁理论，当不考虑热内力时，由式(25)和式(29)可得到

这和材料力学中的公式是一致的。

对应于Timoshenko梁理论，当不考虑轴心压力时，由式(25)和式(29)可得到两端简支和两端固支的热屈曲荷载值。

两端简支

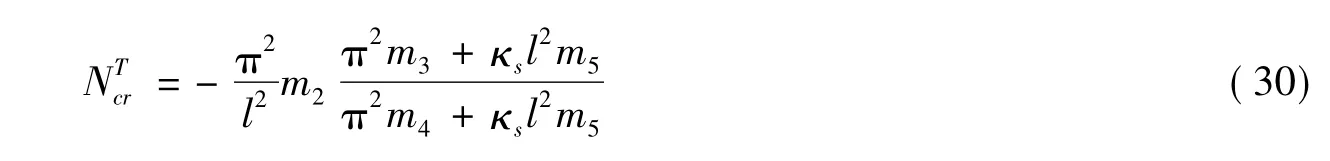
两端固定

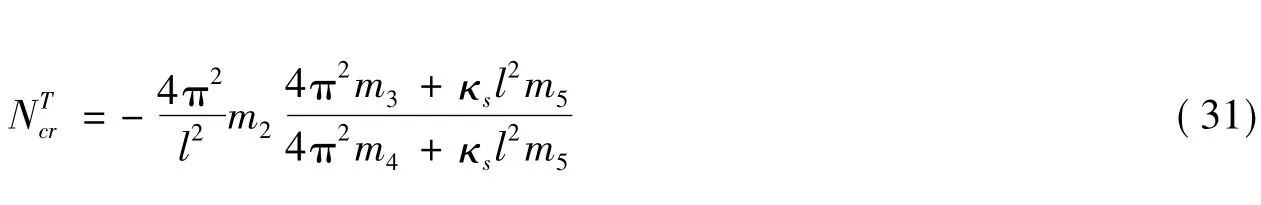
式中，κs为剪切修正系数，经比较式(30)和式(31)的表达式和文献［9］结果相同。

3 理论结果分析

通过上述分析，得到了两端简支梁和两端固支梁的临界屈曲荷载值和后屈曲幅值(梁的横向挠度最大值)，并与相关文献进行了对比分析，可以看出此理论可以包含经典的欧拉梁理论和Timoshenko理论，还能包含各种高阶剪切变形理论。

3．1 长细比对临界屈曲荷载的影响

图1和图2分别给出了不考虑热荷载作用下的两端简支梁和固支梁下不同梁理论下得出的临界屈曲载荷与欧拉梁理论得出的临界屈曲载荷之比随长细比的变化曲线，从图中可以看出，比值随着长细比的增大而增大，各种高阶剪切变形理论计算出的临界屈曲荷载基本相同。而对于两端简支梁:当l/h＞20，计算结果接近欧拉梁理论;两端固支梁:当l/h＞40，计算结果接近欧拉梁理论。

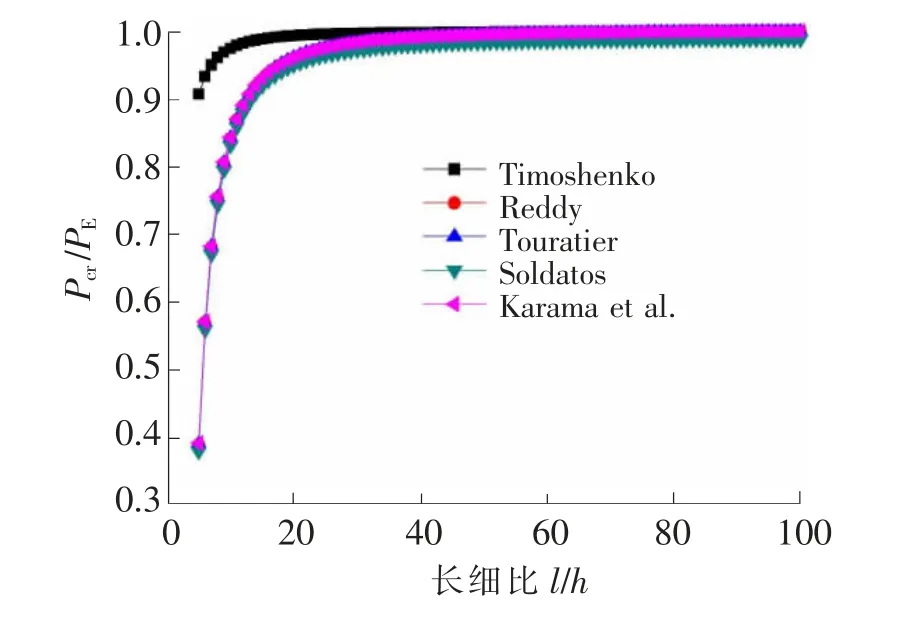
图1 临界屈曲载荷与欧拉梁理论之比随长细比的变化(两端简支梁)

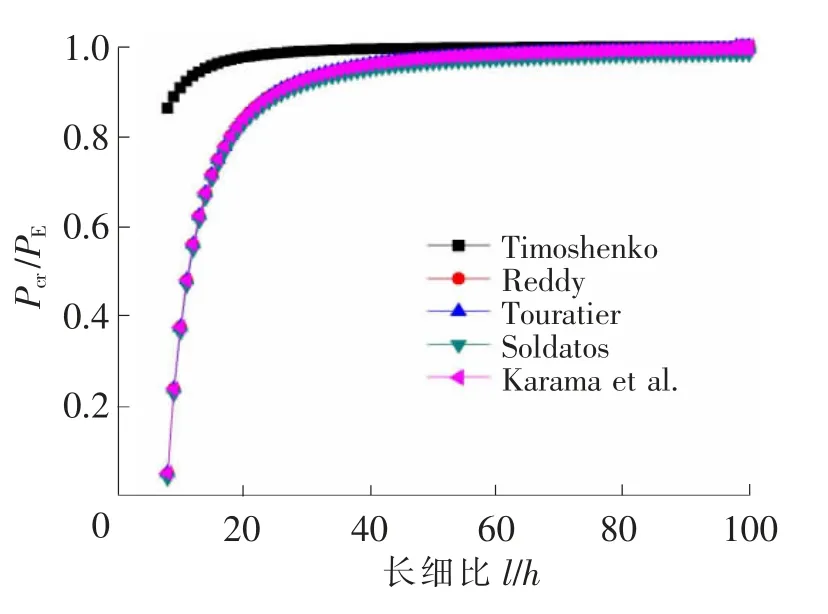
图1 临界屈曲载荷与欧拉梁理论之比随长细比的变化(两端固支梁)

3．2 温度和轴向荷载下对梁后屈曲幅值的影响

为了分析温度和轴向荷载下对梁后屈曲幅值的影响，假定泊松比v=0．3，热膨胀系数a=10－6/℃。为便于分析，以无量纲轴向荷载Pl2/Ebh3为横坐标，梁跨中挠度(a/h)或(2a/h)为纵坐标，得出两端简支梁和两端固支梁分别在不同温度变化下梁的中点挠度与无量纲轴向荷载的变化曲线，图3～图6表明:随着温度升高，梁的屈曲荷载值下降但是梁中点挠度值升高，这是由于梁的刚度削减造成的。

图3 两端简支梁(l/h=10)

图4 两端简支梁(l/h=30)

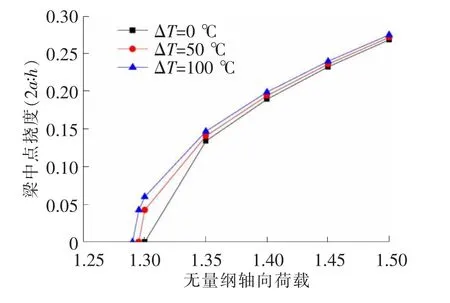
图5 两端固支梁(l/h=10)

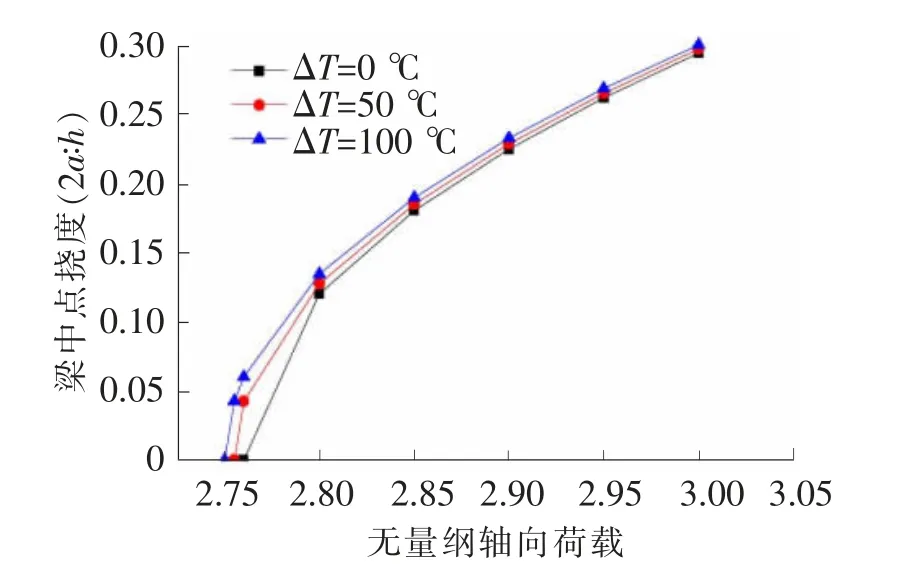
图6 两端固支梁(l/h=20)

4 结论

采用非线性高阶剪切变形理论，分析了两端简支和两端固支边界条件下的梁在不同长细比下的临界屈曲荷载以及温度和荷载下梁的后屈曲幅值。研究表明:①长细比较小时，剪切变形对临界屈曲载荷值的影响很大;随着长细比增大，逐渐接近欧拉梁理论得出的临界屈曲荷载值。②在温度和轴向荷载共同作用下，随着温度升高，梁的临界屈曲荷载值下降，梁中点挠度值逐渐变大。