基于改进模型的异步电机最小二乘参数辨识

孟庆硕，许鸣珠

(石家庄铁道大学 机械工程学院，河北 石家庄 050043)

0 引言

自从矢量控制等高性能变频调速技术的诞生，电机的参数辨识问题便成为了国内外学者的研究热点。矢量控制技术的关键在于转子磁链角的估算，用于实现转子的磁场定向，准确获取转子的时间常数，成为了解决该类问题的关键。但该参数在使用前往往是未知的，因此要实现异步电机矢量控制等高性能变频调速技术，必须预先获得电机的该项参数［1］。

最传统的异步电机参数检测方法莫过于转子空载、堵转和互感实验了，但这样获取的电机参数是粗略的。目前较实用的电机参数辨识典型方法有递推最小二乘法(RLS)、扩展卡尔曼滤波法(EKF)、模型参考自适应法(MRAS)等等。

其中，最小二乘法是常用的参数辨识方法，其目标函数为测量结果对计算结果误差的平方和，最小目标函数值等于零。其递推算法适合于异步电动机参数辨识，计算量也不算很大，但其线性化模型需要用到目标函数对电动机参数的二阶导数，对测量噪声和转速波动很敏感［2-4］。针对这些问题，采用基于转子磁场定向的异步电机同步旋转轴系的矢量方程，建立了电机的转子时间常数参数估计模型，本方法只需要获得一阶导数，同时采用二阶巴特沃思滤波器进行滤波，降低了噪声的影响。利用改进欧拉算法对巴特沃思状态方程进行求解，可以直接得到滤波后电流的一阶导数，不需要对参数进行离散化处理，降低了计算误差。在实际控制中采用双闭环的PI控制，对速度具有较好的控制效果，避免了速度波动对计算的影响。

1 递推最小二乘法参数估计理论

1．1 最小二乘参数估计理论概述

最小二乘法最早于1975年由高斯(K．F．Gauss)在形体运动轨迹预报研究工作中提出来，被广泛应用于系统辨识和参数估计，甚至在许多估计方法无效的情况下，最小二乘法却可以提供最简单有效的解决办法［5-6］。随着该理论的发展，递推最小二乘法、遗忘因子法、偏差补偿法、修正的辅助变量法等多种最小二乘估计算法相继出现，这些方法被应用于不同的系统参数估计系统中。

最小二乘估计算法可以解决线性定常系统、线性时变系统、含有色噪声的线性系统等参数估计问题。在利用最小二乘法对异步电动机进行参数估计时，主要是将电机的非线性模型线性化，得到与电机参数有着直接关系的线性化模型，再对其进行参数估计。

1．2 递推最小二乘法参数估计法

递推最小二乘法应用广泛，与一般的最小二乘法比较，避免了大矩阵求逆运算，计算量小、计算速度快且收敛速度快，可以实现实时在线应用。

由文献［7］～文献［10］可知，递推最小二乘法的参数估计算法为

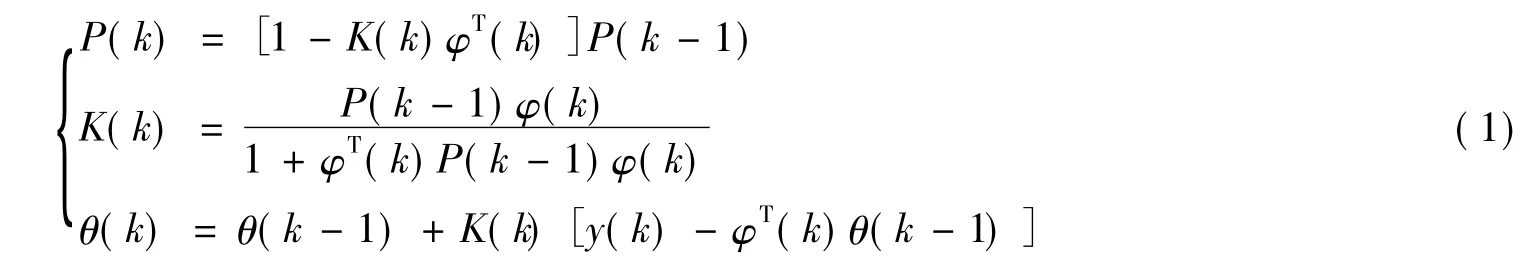
令P(0)=aI，θ(0)=ε，α为充分大的正实数，一般为104～1010之间，ε为充分小的正实数向量，一般取0。

2 异步电机的线性化数学模型

根据文献［11］，可以得到异步电机在任意旋转轴系下的暂态电流导数方程

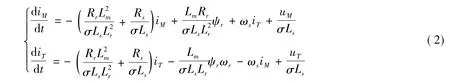
式中，σ=1－(L2m/LsLr);uM、uT为MT轴系定子电压矢量M、T轴分量;iM、iT为MT轴系定子电流矢量M、T轴分量;im、it为MT轴系转子电流矢量M、T轴分量;Rs为定子电阻;Rr为转子电阻;Ls为转子电感;Lr为转子电感;Lm为励磁电感;ωs为转子磁链矢量ψr的电角速度;ωr为转子的电角速度。

将式(2)改写成矩阵的形式如下

其中

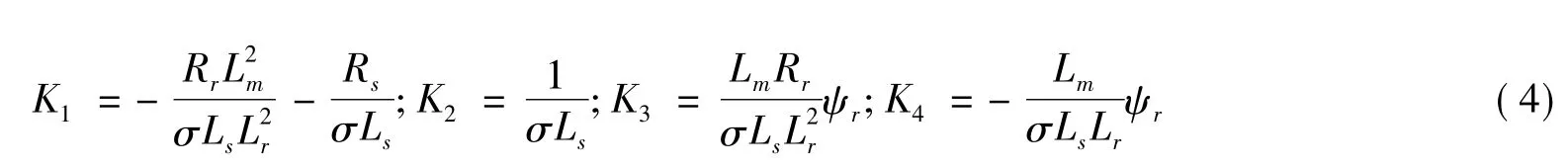
由式(3)可知，经过坐标变换得到了以定、转子电阻、电感、转子磁链为未知量的线性方程，y(k)=φT(k)θ，可运用最小二乘法对电机参数进行估计。输出矩阵

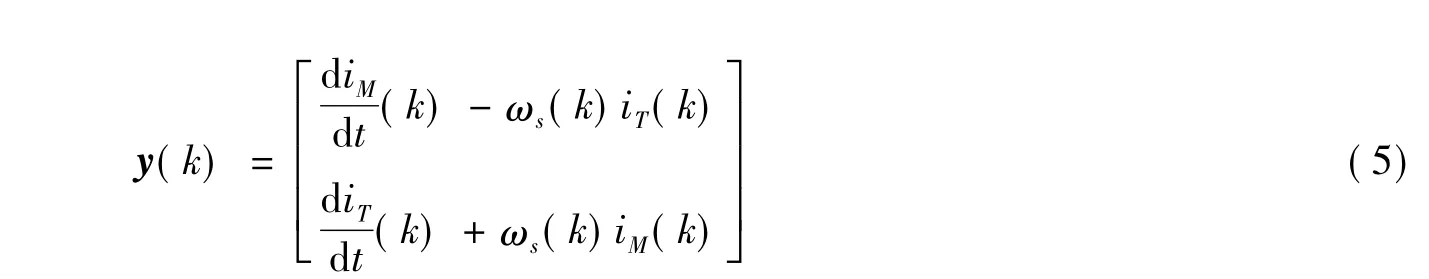
参数矩阵

输入矩阵

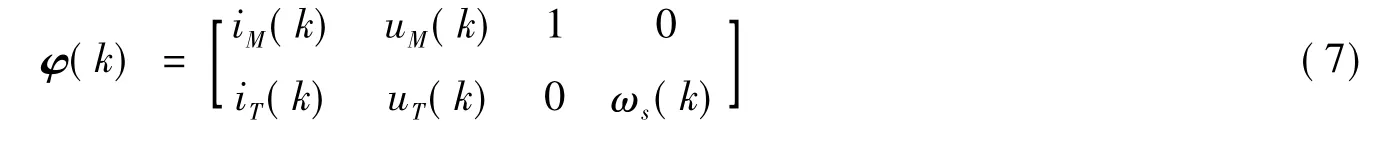
由于参数K3对应的输入为常数1，可能会造成该项收敛速度慢，精度低等缺点。由于K3项中就包含K2项，因此，将K2上次的估计值代替1，此时K3项变为

输入矩阵变为

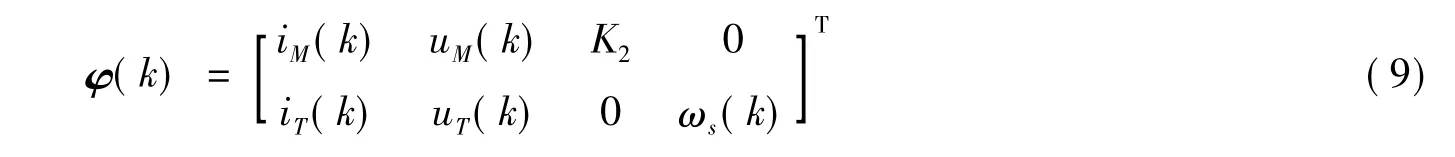
电机的运行往往是由静止到稳态的过程，利用电机的暂态过程可以对电机的转子时间常数Tr=－K4/K3、漏感常数Lsσ=1/K2进行估计。当电机由暂态进入稳态，此时 ψr=0，d iM/d t=0，d iT/d t=0，进而可以根据在转子磁场定向下转子磁链 ψr=－(Rrψr)/Lr+(LmRriM)/Lr得ψr=LmiM，结合估计值θ，进一步求得电机的各参数

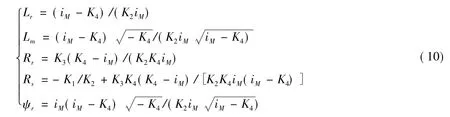
3 巴特沃思滤波器

由于采集的电压和电流信号含有高次谐波和噪声，因此除了硬件上的模拟滤波外，还必须对信号进行数字滤波处理。加入滤波必然造成信号的衰减和时延，为了能够实现对参数的精确估计，电压和电流信号必须同步和同比例采样。这就要求对电压和电流信号要进行相同的滤波。此外，由式(3)可知，在采用递推最小二乘算法参数估计时，除了需要采集电压和电流信号外，还需要得到电流信号的一阶导数。

因此，采用二阶巴特沃思数字滤波器对电压和电流信号进行滤波，二阶巴特沃思数字滤波器的传递函数系数可查表获得。并将其传递函数转换成状态方程形式(13)，写成能控标准型，便于运用改进的欧拉方法进行计算，这样可以直接求解出电流值和其一阶导数。避免了对导数的离散化，简化运算的同时提高了计算精度。

3．1 巴特沃思滤波器设计

巴特沃思低通滤波器的系统函数完全由3 dB截止频率Ωc和阶数N确定。其传递函数为Ha(s)=ΩNc

/DN(s)。其中，分母DN(s)称为N阶巴特沃思多项式

因此，其传递函数为

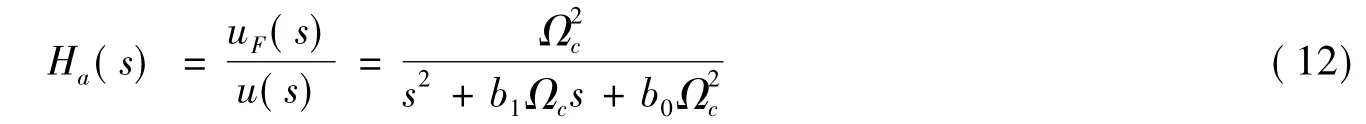
式中，Ωc为低通滤波器截止频率;b0，b1为滤波器系数，可在文献［12］查表获得。

将式(12)转换成状态方程，写成能控标准型

其中

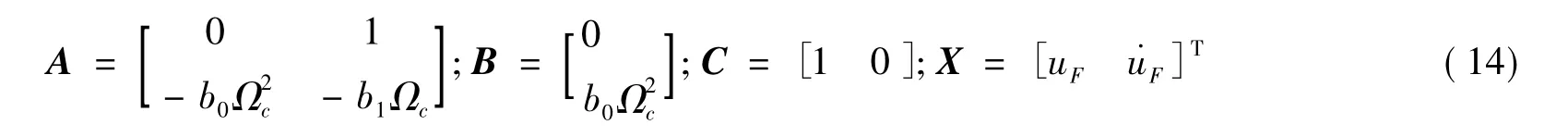
式中，状态变量即为滤波后的电流及其1阶导数。

3．2 改进的欧拉方法

改进的欧拉方法先用Euler格式求得X(k)一个初步的近似值，称为预测值。预测值的精度可能不高，再用梯形公式将它校正一次，得到其校正值［13］。

预测值

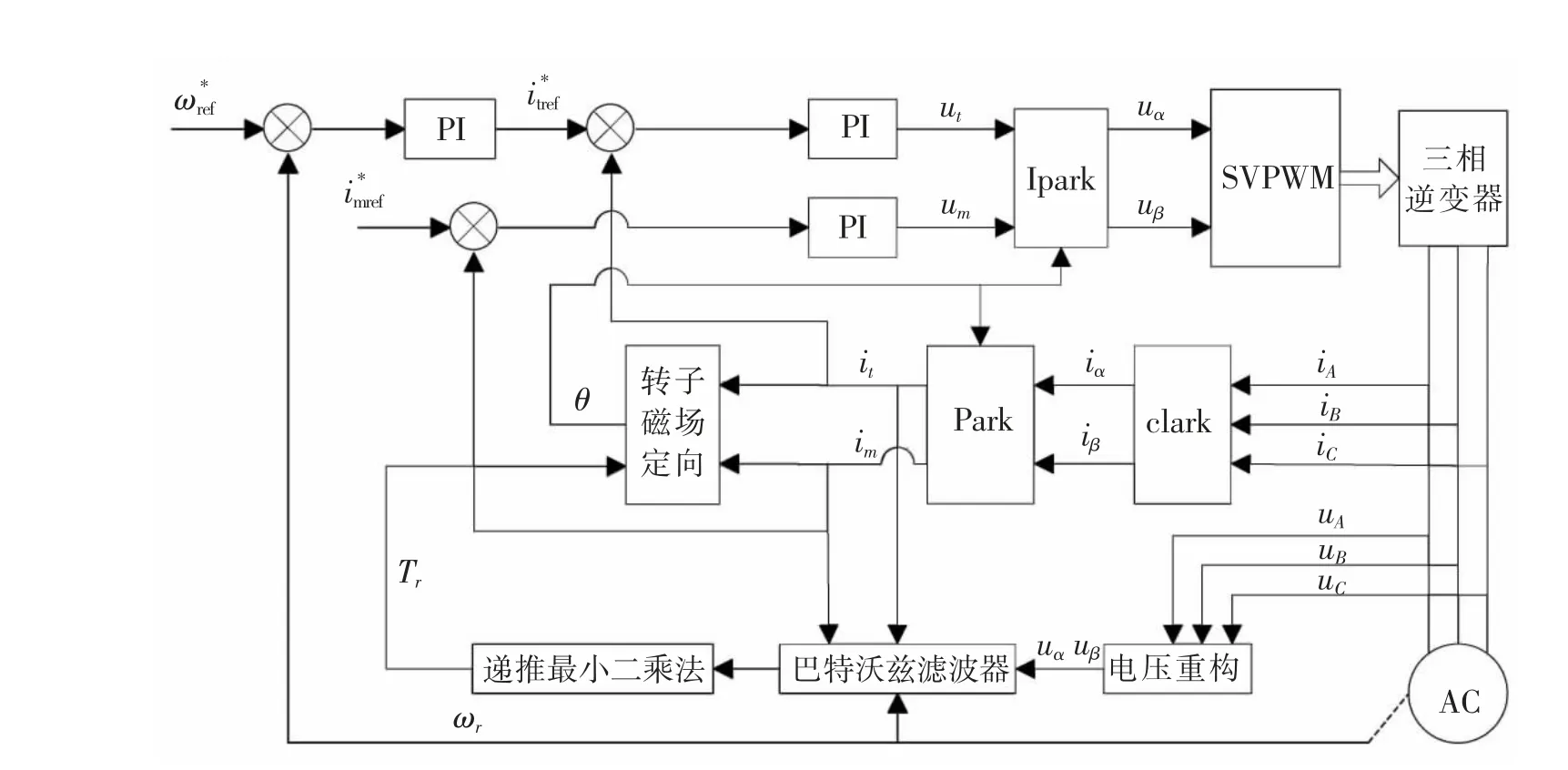
图1 控制系统结构框图

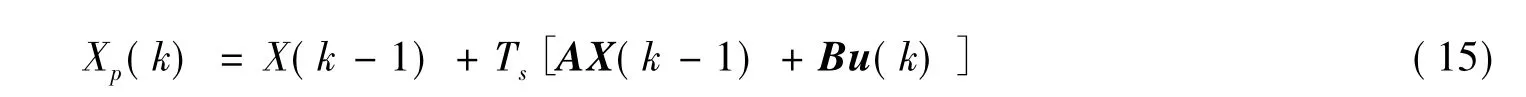
式中，Xp(k)=［uFp(k) uFp(k)］T为状态变量的预估数值解;Ts为采样周期。

由式(15)得到状态变量预估值

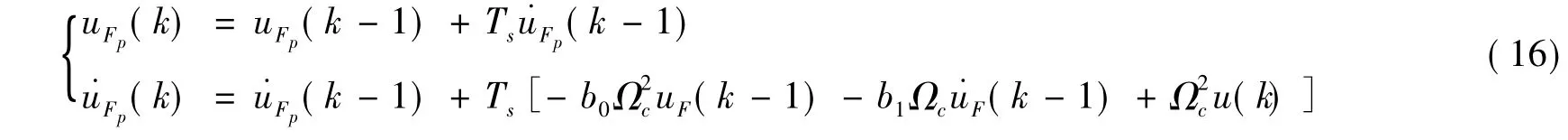
校正值

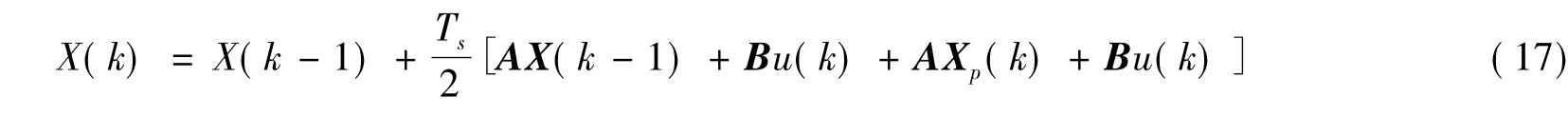
解得状态变量校正值为

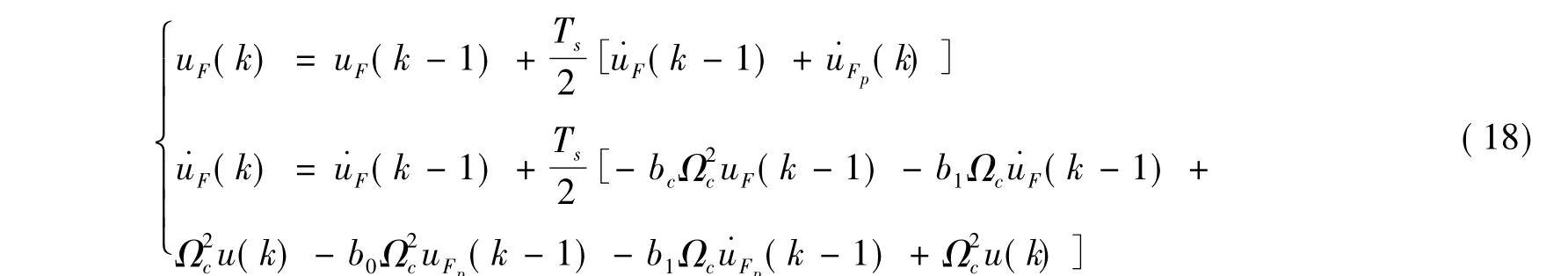
通过对式(18)进行N次迭代即可得到uF(k)，uF(k)即为最终状态变量数值解。

4 实验结果

本文采用异步电机矢量控制实验平台，通过该实验平台来验证所提参数估计算法。整个控制系统采用TI公司的TMS320F2812DSP芯片来实现参数估计算法。

实验用异步电机额定参数为:Pn=250 W;Un=36 V;In=9 A;ωn=1 400 r/min;极对数P=2。DSP系统时钟150 MHz，PWM调制频率为15 kHz。电压信号采样通过测试母线电压，利用电压重构技术得到A，B，C相电压。电流信号采样采用霍尔传感器对其进行测量。采样频率为15 kHz，二阶巴特沃思滤波器的截止频率为10 Hz，迭代次数为10。图1为控制系统结构框图。

本实验是在电机由静止状态运行到额定状态，得到的参数都为电机在额定情况下的参数。从图2～图6可知，在辨识初期电机各参数波动明显，但很快趋于稳定值，证明该辨识系统辨识速度快、稳定性好。表1为转速1 400 r/min时3次辨识的结果，每个参数误差都在5%之内，辨识效果较为准确，对于电机运行控制来说已经达到了足够的精度。

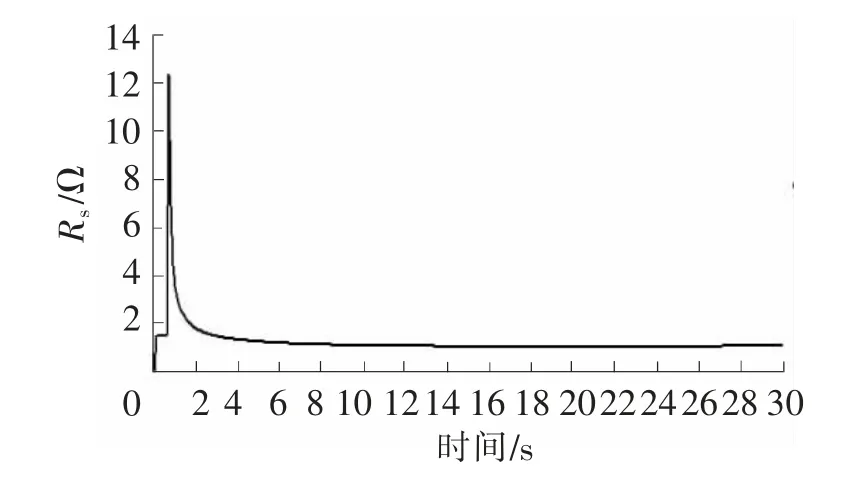
图2 定子电阻辨识曲线

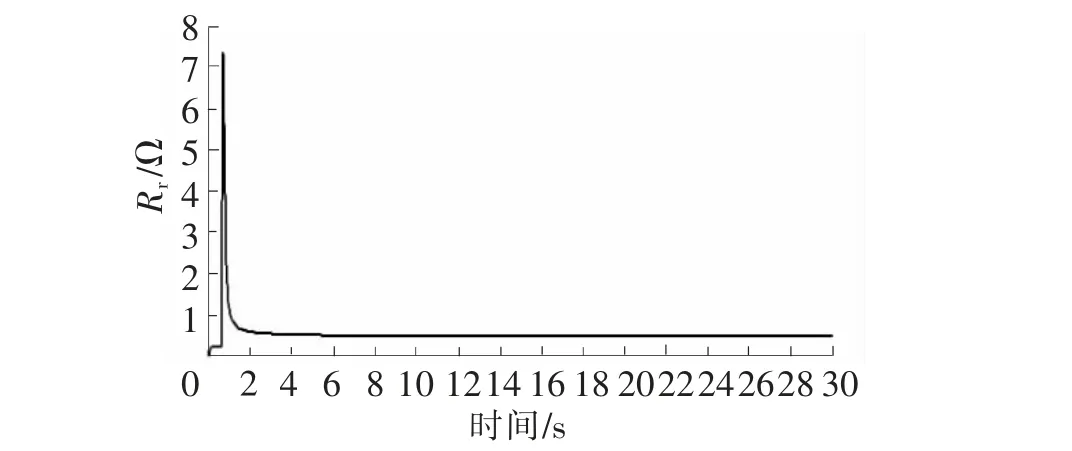
图3 转子电阻辨识曲线

5 结论

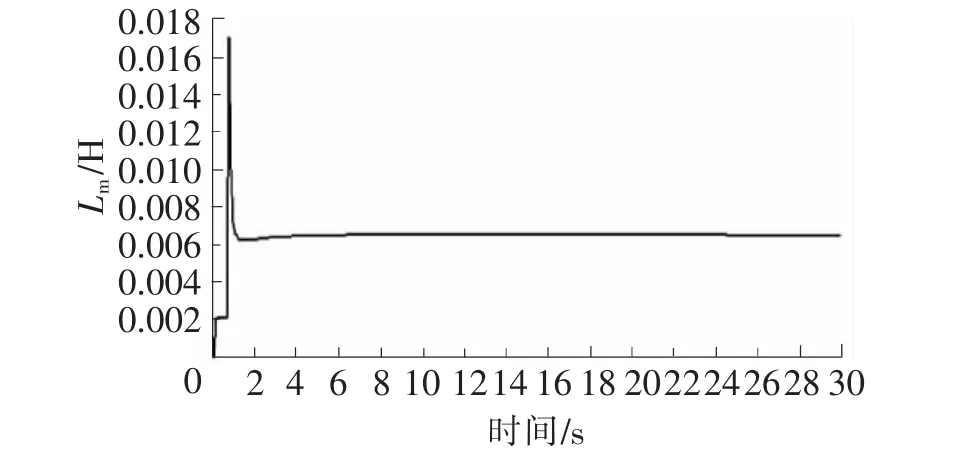
图4 互感辨识曲线

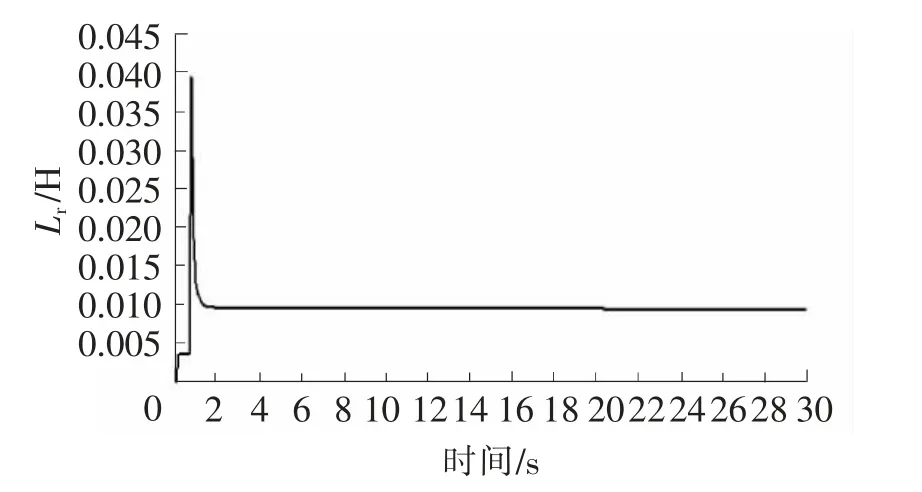
图5 定转子电感辨识曲线

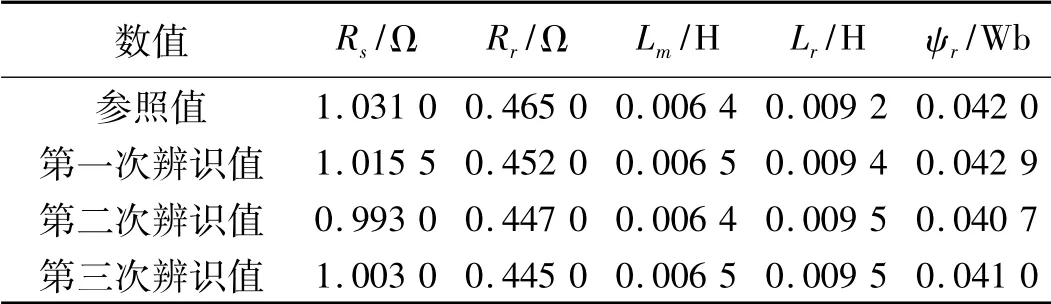
表1 3次辨识结果比较

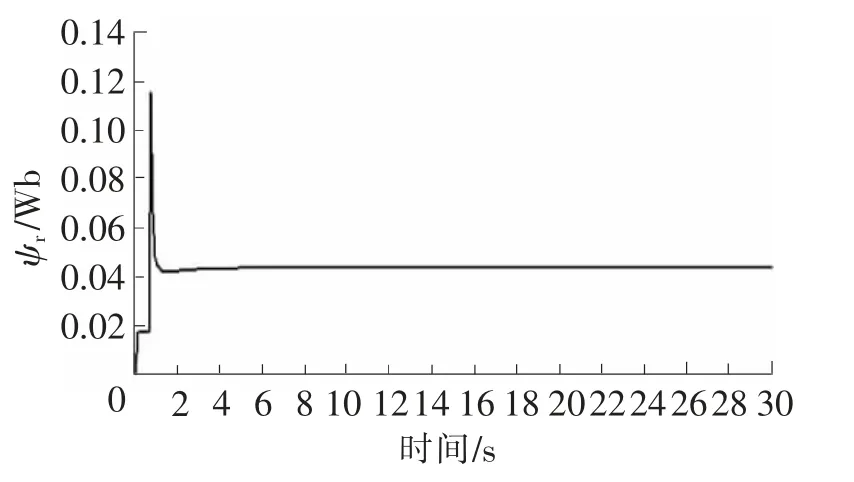
图6 转子磁链辨识曲线

在实验结果中，辨识结果存在着波动，但波动较小。产生波动的原因如下:

(1)采样误差。实验中存在着电磁干扰和噪声的影响，虽然采用了滤波但仍存在不足。滤波器截止频率的选择不合适，对参数辨识结果存在一定的影响，虽然可以通过大量实验选择较为合适的截止频率，但其间的关系还需要进一步研究。另外，由于硬件电路本身也存在误差，也会造成采样不准确，影响参数的辨识。

(2)工况影响。由于辨识出的参数是根据电机运行至稳态下计算得到，此时磁链恒定，经解耦后的电流也恒定，但由于环境的影响，电机的运行状况会受到影响，从而导致电机PI环节对电流进行调整，进而导致电流的变化，造成计算不准确。

本文以转子磁场定向下的同步旋转轴系矢量方程为根据，推导出了可用于递推最小二乘法的线性化电机模型，该模型简单，递推参数收敛速度快。采用二阶巴特沃思滤波器对信号进行数字滤波，并对巴特沃思滤波器的状态方程进行求解，得到了经过滤波后的信号以及信号的一阶导数，无需对导数进行离散化处理，简化了计算，降低了误差，提高了计算精度。