基于耦合混沌振子的微弱信号检测

石兆羽，杨绍普，赵志宏

(1．石家庄铁道大学 机械工程学院，河北 石家庄 050043;2．河北省交通安全与控制重点实验室，河北 石家庄 050043)

0 引言

如今很多领域都需要提取淹没在强噪声中的微弱信号，例如语音处理、生物医学工程、混沌保密通信等［1-2］。传统的信号处理方法忽略了混沌信号的固有几何性质而当做随机噪声进行处理，使得建立的模型精度比较差，从而导致检测微弱信号的能力降低。基于混沌振子的检测方法则利用了混沌的确定性性质来提取强噪声背景中的微弱信号［3］。混沌检测原理简单易行，利用混沌振子对参数及其初值的敏感性及对噪声的抑制性即可检测出微弱信号［4-6］，因此自从Birx et al［7］应用混沌振子检测微弱信号以来，国内外很多学者开始研究该领域，使得混沌检测法得到了不断地发展［8］。目前为止，利用混沌振子可检测的微弱信号类型有方波信号，谐波信号以及任意频率的周期信号，噪声类型有高斯白噪声，高斯色噪声，检测到的信噪比门限比其它检测方法要低得多，可见，应用混沌振子检测微弱信号具有很好的发展前景。

本文研究的是Duffing振子和Van der Pol-Duffing振子通过耦合进行微弱信号检测，首先使用分岔图及二分法确定耦合系统临界值，仿真研究发现该耦合混沌系统具有复杂的动力学行为，能够从强噪声背景中提取出微弱正弦信号，对于混合微弱正弦信号，则能够把不同频率的微弱正弦信号一一检测出来，从而验证了其可行性。

1 建立耦合混沌系统模型

Duffing振子因其自身的非线性动力学特性(振荡、同宿轨道、分岔、混沌和周期)而成为了经典的混沌系统之一，研究Duffing系统的动力学行为有助于进一步了解其性质以及更好地完善混沌理论。以下是经典的Homes型Duffing方程的数学表达式

式中，c为阻尼系数;ax+bx3为回复力;a和b是回复力系数;f1cos(ω1t)是周期策动力，f1和ω1分别是周期策动力的幅值和频率。

Van der Pol-Duffing振荡系统是一种典型的自激励振荡系统，自激极限环振荡系统的原形就来源于它。它的同步现象以及混沌现象是众多学者研究的热点。Van der Pol-Duffing振子作为一种描述振荡过程的基础模型已经在生物学、神经学、物理学和经济学领域广泛应用。Van der Pol-Duffing振子的数学表达式如下

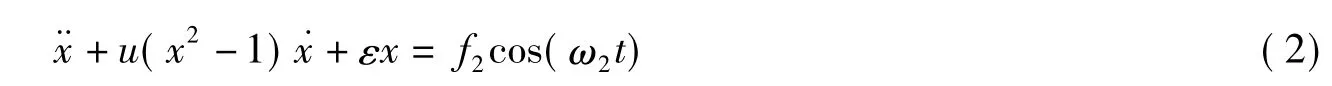
式中，u是阻尼系数;ε是刚度系数;f2cos(ω2t)是周期策动力，f2和ω2分别是周期策动力的幅值与频率。

由于Duffing振子和Van der Pol-Duffing振子均对参数和初值具有敏感性，对噪声具有免疫力，能够有效地提取出淹没在强噪声背景中的微弱信号，因而在微弱信号检测领域，混沌检测微弱信号成为了研究热点［9-15］。通过线性耦合将两振子耦合在一起，对于式(1)，取a=－1，b=1，对于式(2)，取ε=1，对耦合系统作用共同的参考信号f cos(ωt+θ)，ω取值为1，建立的耦合混沌系统如下

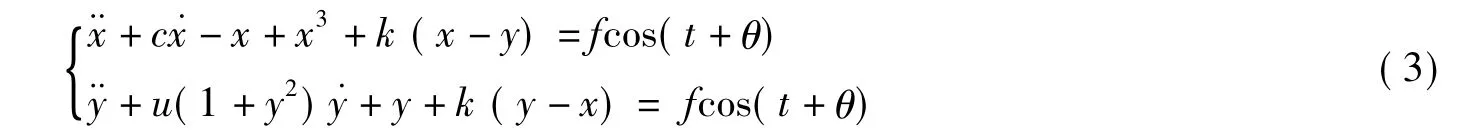
式中，c和u为耦合混沌系统的阻尼系数;k为耦合系数;f cos(t+θ)是参考信号，f是幅值，θ为初相位，通常情况下取0。当其它参数取固定值，耦合混沌系统的状态会随着f的变化而有规律地变化。当f处于临界阈值时，若输入与参考信号同频率(或频率相近)同相位的微弱信号，系统会由混沌态跃迁到周期态，从而完成对微弱信号的检测。

2 分岔图与二分法确定系统精确阈值

选取参数c=0．5，u=1。值得注意的是，当耦合系数k为0时，两个混沌振子的耦合作用就会消失，当k值越大，耦合强度越大，选取参数两振子之间的相互作用就越强。选取k=0．2画出系统分岔图，如图1所示。

由图1可以看出，随着参考信号幅值f的不断增大，耦合混沌系统经历了单周期状态，随后经倍周期分岔进入到双周期状态，经历混沌状态后继续分岔进入四周期状态，然后再次历经混沌状态，最后进入单周期状态。

由分岔图可以看出，耦合混沌系统的临界阈值fe的大致范围在0．75～0．8。当f=0．75时，耦合系统处于混沌状态，f=0．8时，耦合系统处于周期状态，如图2和图3所示。

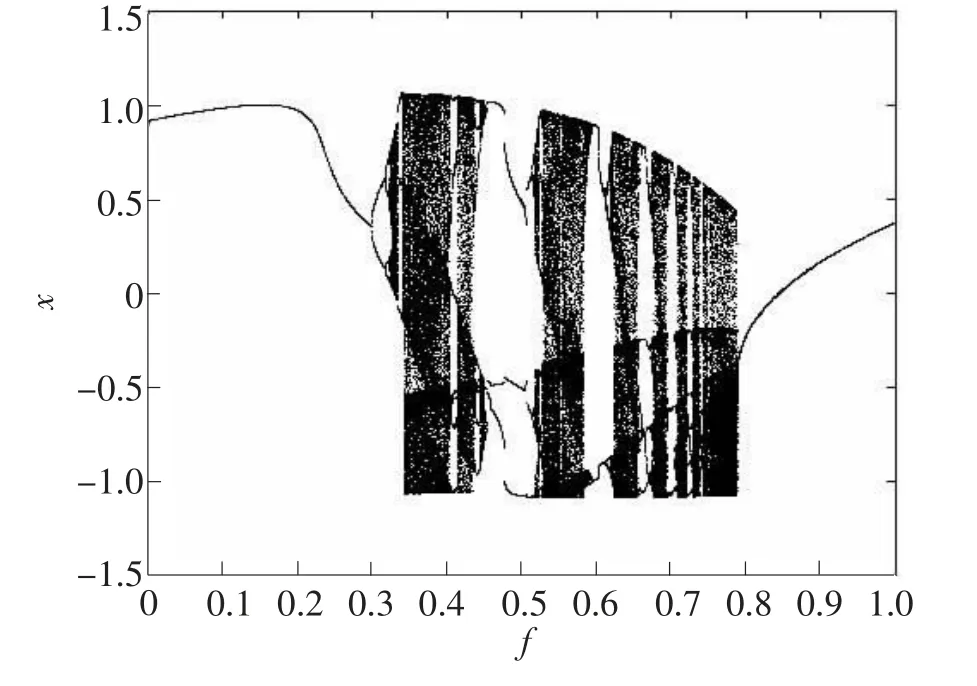
图1 k=0．2时耦合系统的分岔图

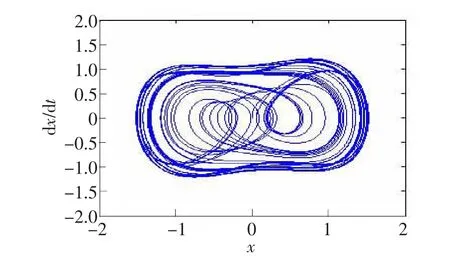
图2 f=0．75时，系统处于混沌态

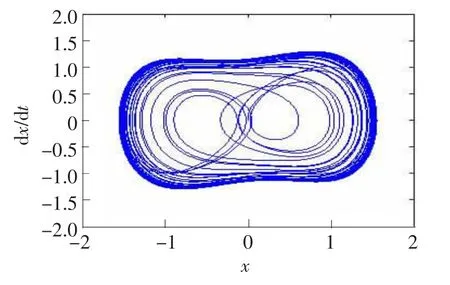
图3 f=0．8时，系统处于周期态

确定了临界阈值的大致范围后，可通过二分法快速搜索系统的精确临界阈值。步骤如下:

(1)由于0．75对应系统混沌态，0．8对应周期态，可取二者的中间值0．775。

(2)通过观察相图可知0．775对应混沌态，所以临界阈值的取值范围为0．775～0．8。以0．01为步长使0．775增加到0．785，该值对应混沌态，0．795对应周期态，再取二者中间值0．79。

(3)0．79对应周期态，临界阈值进一步缩小为0．785～0．79。以步长0．001使f增加到0．789，此值对应混沌态，取0．789和0．79的中间值0．789 5。

(4)0．789 5对应周期态，f的取值范围是0．789～0．789 5。

(5)最终确定耦合混沌系统的临界阈值fe为0．789，0．789和0．789 5所对应的相图如图4和图5所示。

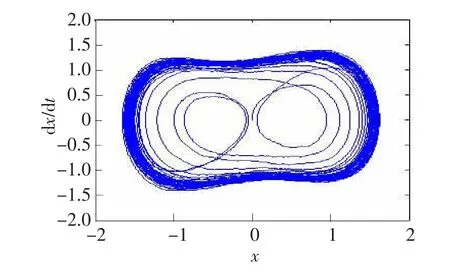
图4 f=0．789时，系统处于混沌态图

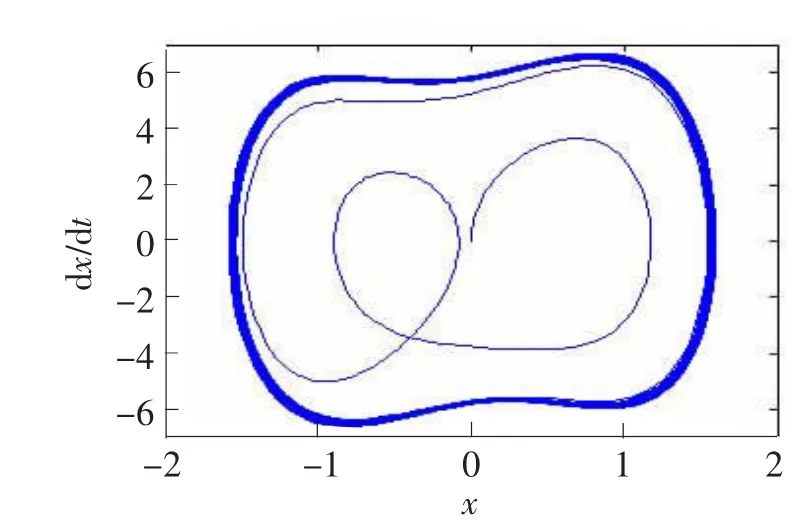
图5 f=0．789 5时，系统处于周期态

通过以上步骤来确定从混沌态到周期态的临界阈值不仅搜索速度快，精确度也较高，证实了二分法能够对临界阈值进行精确定位。为了便于检测任意频率的信号，令t=ωτ，可对式(3)进行时间尺度的变换，得到

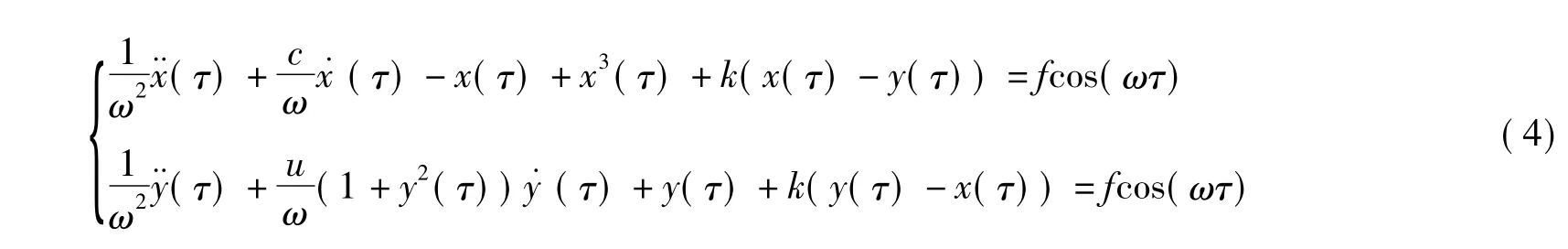
改写成动力学方程为

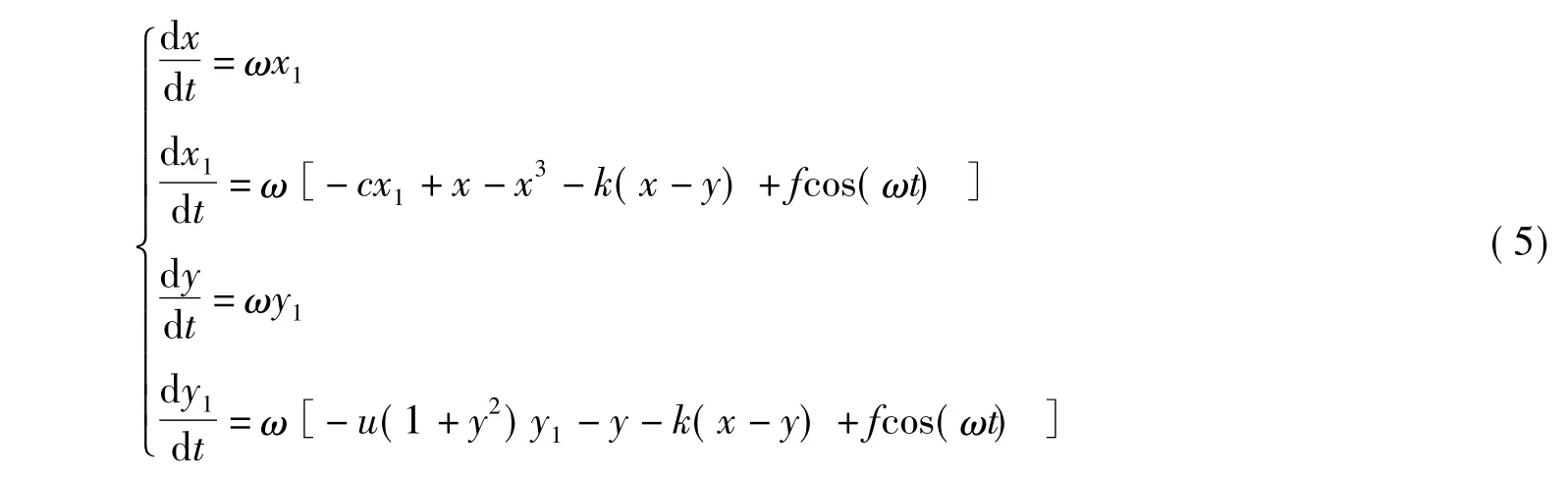
通过上述变换，只需改变式(4)中的ω值，即可检测任意频率的微弱信号。

3 检测单微弱正弦信号

检测微弱正弦信号时，首先调整参考信号幅值f使其处于临界阈值fe，然后将与参考信号同相位，频率相近的微弱待检正弦信号与噪声同时输入到耦合混沌系统，则式(4)变为

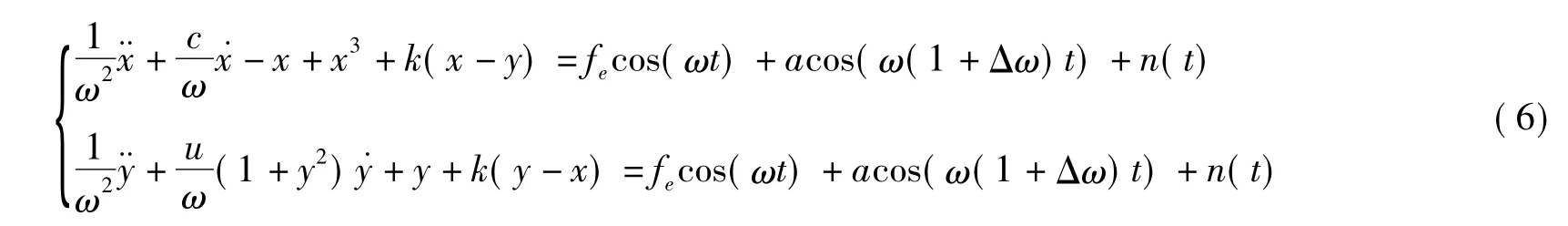
式中，a cos(ω(1+Δω)t)是微弱正弦信号，其中，a是幅值，远小于fe，且a+fe＞fe;Δω是微弱正弦信号与参考信号间的相对频差;n(t)=σ·ε(t)是高斯白噪声。式(6)可简化为

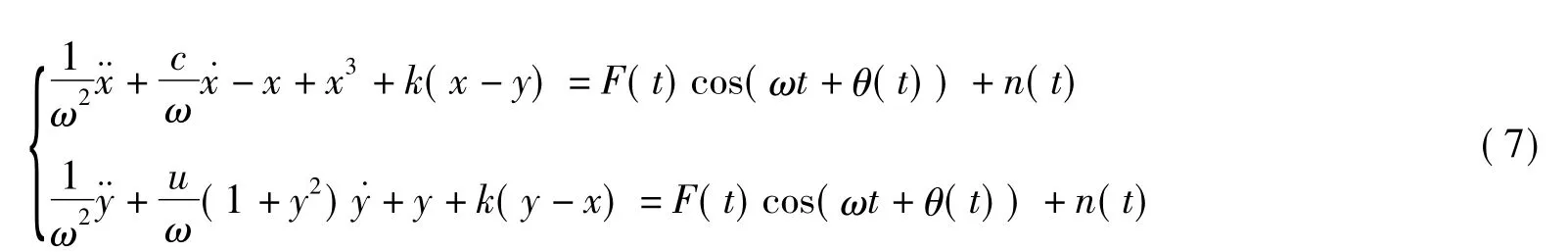
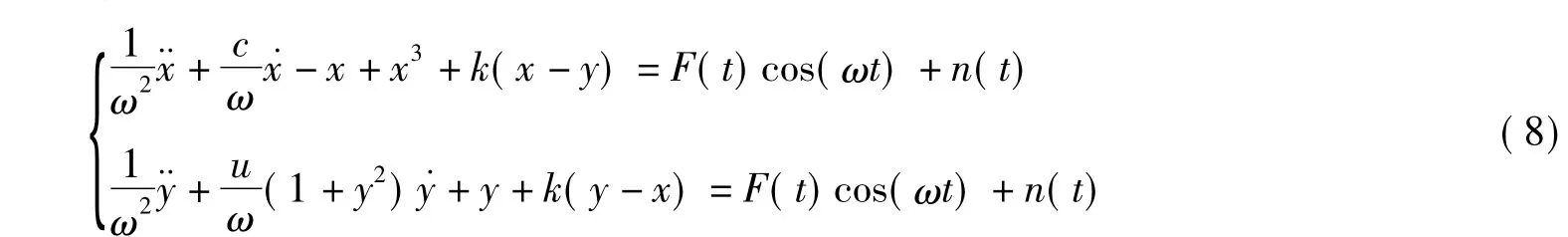
仿真实验表明，待检微弱正弦信号的频率与参考信号的频率的差值Δω的取值不是任意大的，必须在一定范围内，否则无论如何调节，耦合混沌系统都不会从混沌态跃迁到周期态，即此时耦合系统对待检微弱正弦信号免疫，所以要想检测出微弱正弦信号，待检微弱正弦信号的频率与参考信号的频率需满足︱Δω︱≤0．004 rad/s。混沌态到周期态的跃迁过程需要足够长的激励时间，如果︱Δω︱＞0．005 rad/s，会很难辨别阵发混沌现象，F(t)变化的速度也会很快，导致系统不能很好地响应。F(t)＞fe时，由于激励衰减太快，周期运动不会持续，F(t)＜fe时，激励增加太快，混沌运动不稳定，因此，︱Δω︱≤0．004 rad/s。下面给出一个仿真实例。采用四阶龙格库塔法对耦合混沌系统进行simulink仿真，步长h取0．01，ω=1。a=0时，即只输入纯高斯白噪声，σ=0．3，参考信号的幅值设为临界阈值0．789，仿真结果如图6所示。取a=0．000 5，Δω=0．004 rad/s，σ=0．08，f=0．789，仿真结果如图7所示。

对比图6和图7，当把微弱正弦信号和高斯白噪声同时输入到耦合混沌系统，系统状态明显由混沌态跃迁到周期态，验证了混沌理论用于微弱信号检测的正确性。通过simulink仿真，只有当σ≤0．08时，耦合混沌系统才能检测到微弱信号，因此该系统的信噪比门限为:－47 dB。

传统的微弱信号检测方法很难检测到信噪比门限低于－10 dB的信号，而Duffing振子和Van der Pol-Duffing振子耦合的混沌系统能够检测到的信噪比门限为－47 dB，实现了低信噪比下微弱信号检测，因此利用混沌系统检测微弱信号具有很好的研究价值和发展前景。

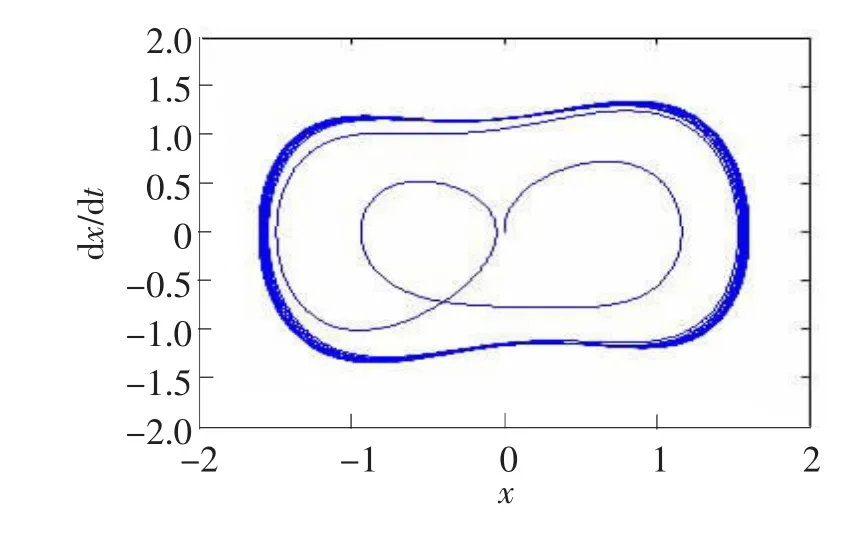
图6 只加入噪声时系统的相轨迹

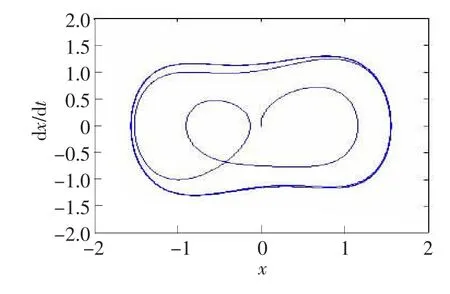
图7 加入待检微弱信号后的相轨迹

4 检测混合微弱正弦信号

实际检测当中，可能存在有不止一个微弱正弦信号，当多个不同频率的微弱正弦信号混合在一起时，如何把不同频率的微弱正弦信号检测出来成为研究的一个要点。混合微弱正弦信号之间的频率可能相差很大，又或者很小。当输入两种频率相差很大的微弱正弦信号时，设输入系统的混合微弱正弦信号为s=s1+s2=a cos(ω1t)+b cos(ω2t)，式(6)变为

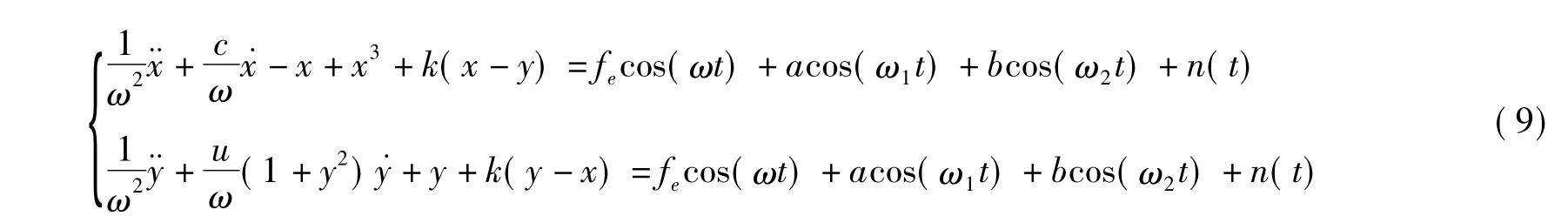
选取ω1=5 rad/s，ω2=15 rad/s来进行仿真。根据本文第3节的分析，当参考信号的频率ω与微弱正弦信号的频率ω'满足0．996ω≤ω'≤1．004ω时，才能使处于临界状态的耦合混沌系统对微弱信号敏感，对于频率与参考信号频率相差很远的微弱正弦信号不敏感。所以，要检测出微弱正弦信号s1和微弱正弦信号s2，只需将参考信号频率设置在5 rad/s，由于15 rad/s不在［0．996ω，1．004ω］=［4．98，5．02］的范围中，当输入混合信号时，微弱正弦信号s2与噪声并不会改变系统的状态，而微弱正弦信号s1会使耦合混沌系统由混沌态跃迁到周期态，从而将微弱正弦信号s1检测出来。如图8所示。

同理，当检测微弱正弦信号s2时，设置参考信号频率为15 rad/s，此时耦合混沌系统对微弱正弦信号s1免疫，输入微弱正弦信号s2时，耦合混沌系统会由混沌态变化到周期态。因此，如果有多个不同频率的微弱信号同时输入到系统，只需根据微弱信号的频率调节参考信号的频率就可以将它们一一检测出来。但在实际情况中，多个微弱信号之间存在频率相互接近的可能，此时系统即使发生相变也无法判断是哪个频率的微弱信号对系统产生了影响，因此会出现误判的情况。

当混合微弱信号之间的频率相差很小时，设输入系统的混合微弱信号为s'=s3+s4=c cos(ω3t)+d cos(ω4t)，本文选取ω3=0．6 rad/s，ω4=0．602 rad/s进行simulink仿真。为了能够检测到上述频率的微弱信号，需将ω3和ω4设置为参考信号的频率。因为参考信号的频率ω与微弱正弦信号的频率ω'满足0．996ω≤ω'≤1．004ω，所以耦合混沌系统能检测的频率范围为［0．597 6，0．602 4］和［0．599 6，0．604 4］，但是ω3=0．6 rad/s和ω4=0．602 rad/s都在这两个检测范围内，当系统出现相变时，并不能判断检测到的微弱信号是s3还是s4。为了能够准确判断系统由混沌态转变为周期态是哪个频率的微弱信号所导致的，需要重新选择一个合适的参考信号频率，使得ω3和ω4不会在两个检测范围内。令

ωm=0.601。将ωm设置成参考信号的频率，则其检测范围为［0．598 6，0．603 4］，再将0．598 6和0.603 4分别设置成参考信号的频率，则它们的检测范围为［0．596 2，0．601 0］和［0．601 0，0．605 8］，这时ω3和ω4只满足一个检测范围。因此检测微弱信号时首先将参考信号的频率设置为0．598 6 rad/s，此时耦合混沌系统只对微弱正弦信号s3敏感，对微弱信号s4免疫，如图9所示。

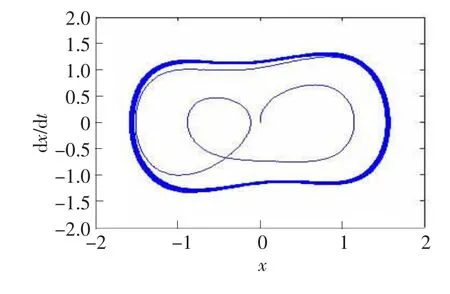
图8 微弱信号s1作用下系统的相轨迹

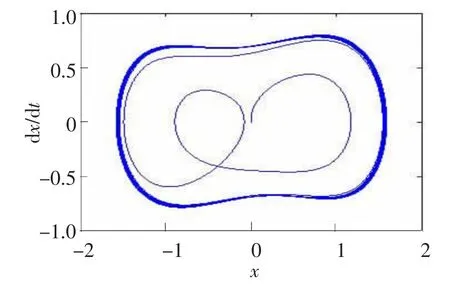
图9 微弱信号s3作用下系统的相轨迹

同理，参考信号的频率设置为0．603 4 rad/s，在微弱正弦信号s4的作用下，耦合混沌系统完成由混沌态到周期态的转变，微弱正弦信号s3不影响系统的相变，从而检测出微弱正弦信号s4。

讨论了如何检测混合微弱正弦信号(两种不同频率的微弱信号)，当两频率相差很大或两频率很接近时，都进行了实例仿真，证实了本节方法是可行的。当两个以上的微弱正弦信号输入到耦合混沌系统，其检测原理也是相同的。

5 结论

本文建立了Duffing振子和Van der Pol-Duffing振子耦合的混沌系统，提出了通过分岔图和二分法来确定系统精确的临界阈值，通过分析可知该方法可行。对单微弱正弦信号进行检测，信噪比门限达到了－47 dB，比单混沌振子的最低信噪比门限还要低，最后阐述了如何检测混合微弱正弦信号，获得了较好的效果。