分类讨论思想在数学教学中的运用

广东省东莞市石龙第三中学(523323) 王烈群

义务教育数学课程标准指出:”数学思想在义务教育阶段应结合教学内容进行逐步渗透,是把知识型教学转化为能力型教学的关键,是实施素质教育的重要组成部分.”分类讨论就是其中一种重要的数学思想.分类讨论思想是按照某一标准将研究问题划分为不同类别,逐类研究获取每类结论,最后综合各类结论解答整个问题.分类讨论的一般步骤:1⃝明确分类对象;2⃝对问题中的若干条件依据同一标准进行合理分类,做到不遗漏、不重复,然后逐步讨论所分种类,分级进行以得到各类讨论结果;3⃝归纳总结各类讨论结果.

分类讨论思想能够将复杂问题简单化,化繁为简,既做到将教学内容条理化又清楚的呈现出问题本质,更易于解决问题.它揭示了数学对象之间的内在规律,有助于学生逻辑思维的养成和归纳总结能力的提高.分类讨论思想是一种重要的数学思想,也是一种解决问题的逻辑方法.

教师在概念教学渗透分类讨论思想,提高学生的数学思维能力.

1.概念教学渗透分类讨论,突显概念本质

数学中的许多概念的定义是分类给出或有一定的限定,教师可以通过启发引导,在概念教学中渗透分类讨论思想,让学生逐步体会分类讨论,突显概念本质.

例1人教版九年级上册第3页,一元二次方程的概念中对二次项系数的限定

一元二次方程一般式ax2+bx+c=0(0)中涉及0的规定.教学中,为了让学生更深刻地理解概念中0,可以让学生进行分类讨论.当a=0时,方程变形为bx+c=0,没有二次项,因此不是一元二次方程,若此时,0,此方程就为一元一次方程,若b=0,则此等式不是关于x的方程.当0时,方程中才还有二次项,才能成为一元二次方程.这样学生能够更深刻地理解一元二次方程概念中二次项系数0的条件限定.

在初中数学教学内容中,还有许多数学概念的定义,如实数和有理数的分类、绝对值的化简、一元二次方程的概念中对二次项系数的限定、平方根中对于被开方数的限定、点与圆、直线与圆的位置关系……都渗透着分类讨论的数学思想.教师在概念教学中渗透分类讨论思想,让学生对分类讨论思想有正确的认知、理解、掌握和运用.

2.法则、定理、性质或公式教学中渗透分类讨论,培养学生良好思维能力

在法则、定理、性质或公式中也常常需要分类讨论,教师在教学中渗透分类讨论思想可以培养学生良好思维能力.

例2人教版九年级上册第10和第11页一元二次方程ax2+bx+c=0(a0)根的判别式

一元二次方程ax2+bx+c=0(0)的实数根,判别式∆=b2−4ac.由于一元二次方程的实数根中被开方数含未知数,所以要进行分类讨论.

当∆>0时,方程有两个不相等的实数根;当∆ =0时,方程有两个相等实数根;当∆<0时,方程没有实数根.

在教学中渗透分类讨论思想,让学生对一元二次方程根的判别式有更深刻地认识,也培养了学生良好的思维能力.

3.问题解决教学中强化分类讨论,培养学生良好思维习惯

问题解决中常见的分类讨论主要有以下两类:(1)代数型分类讨论,含有字母系数或参数的问题,有时需讨论该字母的不同取值范围;如绝对值化简,方程根的个数,函数的图像和性质,二次函数最值等;(2)某些不确定的结论、不确定的图形的位置或形状以及不确定的数量等需进行分类讨论.几何型分类讨论,如求等腰三角形第三边,直角三角形的第三边,相似三角形的分类讨论等.

例3.1人教版八年级数学上册习题13.3第81页1(2)题

(2)等腰三角形的一个角是80◦,它的另外两个角是多少度?

题目中没有指明这个角是底角还是顶角,所以已知角按照底角和顶角两种情况进行分类讨论.

解①当这个角是底角时,另外两个角是:80◦,20◦;

②当这个角是顶角时,另外两个角是:50◦,50◦.

答:另外两个角是:80◦,20◦或 50◦,50◦.

该问题解决中不明确已知角是底角还是顶角,因此,已知角按照底角和顶角两种情况进行分类讨论.对题目进行分类讨论,可以让学生养成良好思维习惯.

例3.22018年广东中考数学试题23题第三小问中涉及分类讨论思想

23.如图1,已知顶点为C(0,−3)的抛物线y=ax2+b(0)与x轴交于A,B两点,直线y=x+m过顶点C和点B.

(1)求m的值;

(2)求函数y=ax2+b(0)的解析式;

(3)抛物线上是否存在点M,使得∠MCB=15◦?若存在,求出点M的坐标;若不存在,请说明理由.

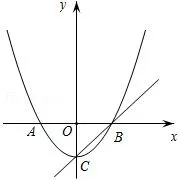
图1

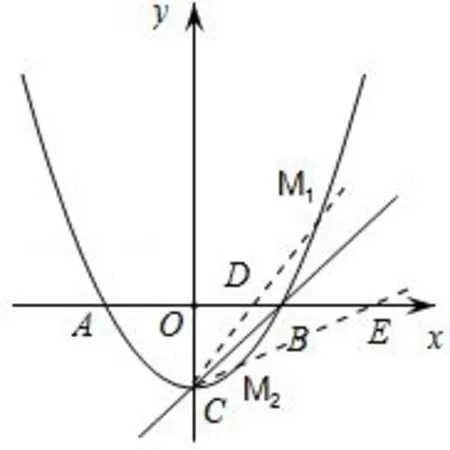
图2

(3)分M在BC上方和下方两种情况进行解答即可.因为题目要使得∠MCB=15◦,所以点M不在BC上,故M在BC上方或者下方,因此,分两种情况进行分类.

解(3)存在,分以下两种情况:

若M在BC上方,设MC交x轴于点D,则∠ODC=45◦+15◦=60◦,所以,设DC为y=kx−3,代入,可得:,联立两个方程可得:解得:,所以;若M在BC下方,设MC交x轴于点E,则∠OEC=45◦−15◦=30◦,所以设EC为y=kx−3,代入可得:解得:,所以,综上所述M的坐标为.

初中数学教学中渗透分类讨论思想,是新的课程标准的要求,也是进行数学素质教育的一个切入点.初中数学教学中渗透分类讨论思想,有利于提高学生对学习数学的兴趣,有利于学生从深层次地理解和掌握数学知识,有利于培养学生思维的条理性、缜密性、科学性,有利于学生养成良好的数学思维习惯.