两类异质混沌系统的同步研究

(1) 山东师范大学数学与统计学院，250358，济南； 2) 齐鲁师范学院数学学院，250014，济南)

1 引 言

混沌系统的同步理论是非线性科学的研究热点，在众多领域中有重要的实际应用价值.综合已有的研究成果[1-4]我们发现，其主要研究基础是连续动力系统理论，通过建立系统间的误差系统，利用李雅普诺夫稳定性理论来研究误差系统的渐近稳定性.当无法有效建立误差系统时，上述方法就失效了.2005年，Luo提出了不连续动力系统理论[5]，并取得了一系列的研究成果[6-10].将该理论应用于同步问题的研究能克服利用连续动力系统理论方法存在的不足，并且对不同约束条件下不同类型的同步问题均可得到有效的分析结果.2014年，Sun和Fu研究了在正弦约束下Van der Pol方程与单摆方程的混沌同步问题[11].2015年，孙晓辉[12]利用不连续动力系统理论研究了一类异质二阶多自主体系统的一致性问题，给出了两个系统部分时间一致性开始和消失的解析条件.在此基础上，本文将研究陀螺仪系统与具周期外力的单摆系统的同步问题，并建立相应的同步条件.

2 模型分析

选取具有周期外力的单摆方程作为主动系统(master system)

(1)

陀螺仪方程作为被动系统(slave system)

(2)

其中σ(y)=-α2(1-cosy)2/sin3y.

将m-系统写为向量形式

(3)

取函数Ξ为控制条件，其中Ξ(X,Y,t)=(ξ1,ξ2)T,ξ1=k1sgn(y1-x1),ξ2=k2sgn(y2-x2).那么在此控制条件下s-系统为不连续系统，从而

(4)

由于两个系统是独立的，m-系统的流不受影响，不会发生变化.但是两个系统要达到同步，s-系统的流受会到m-系统流的影响.基于以上控制条件，受控s-系统的相空间可分为如下的四个子区域Ωj(j=1,2,3,4):

由于控制条件的影响，受控s-系统在不同子区域内的动力学方程是不同的，比如在Ω1内为

类似的，可给出其它三个子区域上受控s-系统的表达式.

受控s-系统的四个子区域之间的边界为

各边界的交点是

由此可见若要两个系统的动力学行为一致，同步只能在各边界的交点处发生.

下面利用不连续动力系统的方法，将受控s-系统表示为以下形式

(5)

其中

边界是由m-系统决定的，边界上的子系统定义为

(6)

其中

由于各区域之间的边界是随时间变化的，直接建立相应的解析条件较为困难，因此下面采用相对坐标形式进行研究.令z1=y1-x1,z2=y2-x2.于是，

相对坐标下受控s-系统为

(7)

边界上的系统为

(8)

3 主要结果

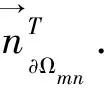
(9)

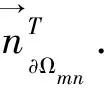
(10)

于是，边界上的法向量和相应的G函数分别为(j=1,2,3,4.)

其中

为方便起见，定义如下的基本函数:

(i) 当(m,n)={(2,3),(4,1)}时，

(ii) 当(m,n)={(1,2),(3,4)}时，

则受控s-系统的同步将消失.

证由不连续动力系统的流转换理论[5]可知，系统在零点形成同步(Zk=0)的条件是

根据g1,g2,g3,g4的定义, 上述同步条件变为

其它情形的证明类似可得.

(i) 当(m,n)={(2,3),(4,1)}时,

(ii) 当(m,n)={(1,2),(3,4)}时,

则受控s-系统开始达到同步.

上述定理的证明与定理1类似，在此略去.

其中L-函数为

由以上分析可知，同步现象的不变域可以由-k1

0≤z2

当参数k1和k2适当选择时，可以得到系统间不同状态的同步情形.

4 数值仿真

图1 系统的不变集

图2 m-系统轨线与不变集的位置关系

下面对系统里的参数取值分别为a0=-1,A0=0.23,ω=1.187 9,c1=0.5,c2=0.05,α=10,β=1,f=35,Ω=2,x1=y1≈0.779 2,x2=y2≈0.512 7.对于控制条件中的参数先选取k1=5,k2=100,则系统的不变集如图1所示.在上述参数选择下，首先给出m-系统的轨线与不变集之间的位置关系(图2).显然轨线完全落在不变集内部，但是否能够形成完全一致性则需要对达到同步的条件进行验证.由图3可以看出四个gi函数是没有转换点出现的，满足了达到同步的条件，因此可以判定此时系统出现完全同步.图4给出了取定参数后，两个系统间位移与速度的关系，从图中可以看出，两个系统能够达到完全一致性，并始终保持.但是当参数k1,k2的取值变化时，同步情形将发生变化.下面取k1=5,k2=40.从图5可以看出，系统的轨线无法完全落在不变集中，因此即使在不变集外满足相应条件也无法保证系统间的同步.对此情况进一步判断gi函数的情形.由图6可以看出，此时一定会有满足定理结论的同步开始和消失的转换点存在，因此在此情况下系统间不可能达到完全同步.这就需要利用结论中建立的条件对转换点的情况进行分析，判断系统在什么时间范围内能够形成同步，什么时间同步消失，最终得到系统间的部分同步情形.最后对两个系统轨线的关系进行模拟.从图7可以看出，两个系统的位移无法形成完全同步，由于存在转换点同步会在某些点处消失，然后在控制条件的作用下于某一满足转换条件的点处再次形成同步.这也说明关于位移的模拟与之前理论分析的结论是一致的.

图3 gi(i=1,2,3,4)函数图像(k1=5,k2=100)

图4 位移与速度的完全同步

图5 m-系统轨线与不变集的位置关系

图6 gi(i=1,2,3,4)函数图像(k1=5,k2=40)

图7 位移的部分同步图