指数平方损失下变系数部分非线性模型的估计

(山东师范大学数学与统计学院,250358, 济南)

1 引 言

本文考虑一个重要的半参数模型—变系数部分非线性模型, 其模型形式为:

Y=ZTα(U)+g(X;β)+ε,

(1)

其中α(·)=(α1(·),...,αp(·))T是未知系数函数的p维向量,g(·;·)是预先指定的函数,β是未知参数函数的d维向量,ε是独立于(ZT,U,XT)T的随机误差并且E(ε)=0.

近年来, 关于变系数部分非线性模型的统计推断得到广泛关注. 例如, 文献[1]提出了一种轮廓非线性最小二乘估计, 并进一步引入了广义似然比检验, 去检验模型中的变系数是否为常数. 文献[2]提出了两阶段估计程序, 他们首先基于正交投影方法去估计参数系数, 然后用B样条基函数逼近每一个变系数函数. 文献[3]应用似然方法去推断参数和非参数部分. 但是这些方法都是基于最小二乘方法提出的, 对异常值非常敏感. 最近, 文献[4]基于指数平方损失对一般线性模型进行一系列的稳健估计, 证明了所提出的估计方法不仅能保持高稳健性, 而且在正态误差条件下, 与无异常值的最小二乘方法一样, 得到很好的估计结果. 文献[5]对变系数部分非线性模型应用指数平方损失方法进行估计, 它们对变系数部分进行局部多项式展开, 分两步进行估计, 并提出新的MM算法去计算非参数和参数部分的估计, 得到不错的结果. 但是分两步估计, 计算量很大.

在本文中, 受文献[4]和文献[5]的启发, 我们对模型(1)也使用指数平方损失方法, 对未知参数进行稳健估计, 但是我们对变系数部分采取B样条基函数逼近的方式展开, 这样变系数部分可以写成线性组合表示的形式, 便于计算和估计. 并在一定正则条件下, 建立了估计量的渐近性质.

2 估计方法

(2)

其中h是调节参数, 它控制着估计的稳健性和有效性.

(3)

3 估计的渐近性质

为了建立所提估计的渐近性质, 本文提出以下正则条件, 其中C表示正常数, ‖·‖代表2-范数.

条件1 指示变量U有有界支撑Ω并且它的密度函数fU(·)是正的, 还有连续的二阶导数, 不失一般性, 我们假设Ω是单位间隔[0,1].

条件2 变系数函数α1(u),...,αp(u)在[0,1]上是r次连续可微的, 并且r>2.

条件3 令Σ1(u)=E{ZZT|U=u},Σ2(u)=E{g′(X;β)g′(X;β)T|U=u}关于u是连续的, 此外, 对于给定的u, Σ1(u)和Σ2(u) 是正定矩阵, 并且他们的特征值是有界的, 除此之外, 假设

条件5F(z,x,u,h)和G(z,x,u,h)关于(z,x,u)是连续的.

条件6 对任意的h>0, 都有F(z,x,u,h)<0.

条件8g(·;β)是关于β的连续函数,g(·;β)关于β的二阶导存在并且连续.

记α0(·)和β0分别是α(·)和β的真实值, 有下面的定理1和定理2成立.

定理1 假设正则条件1至条件6成立, 并且k=O(n1/(2r+1)), 那么我们有

定理2 假设正则条件1至条件8成立, 并且k=O(n1/(2r+1)), 那么我们有

其中定理和定理证明中所使用的符号表示如下：

4 估计性质的证明

我们首先证明, 对于任意给定的η>0, 存在C使得

(4)

通过泰勒展开, 我们有

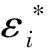
类似的我们能得到I3=Op(nδ3k-1‖V‖3), 因为δ=n-r/(2r+1)→0, 当‖V‖=C时,δ‖V‖→0.因此,I3也被I2控制住.

(5)

定理1的结论(1)证明完成, 下面证明定理1的结论(2).

4.2定理2的证明在定理1的证明中可以看到, 当n→时, 概率趋于1. (3)式中的l(γ,β)在和处获得最大值, 通过计算, 我们有

通过简单的计算及泰勒展开, 有

(6)

类似地,有

(7)

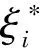
那么, 根据正则条件3和条件7, 基于等式(7), 经过计算有

(8)

将式(8)代入式(6)中, 我们得到

注意到

通过(8)很容易得到

(9)

利用大数定律, 有

(10)

利用中心极限定理, 有

(11)

联合(10)和(11), 应用Slutsky定理, 有

定理2证明完成.