Cattaneo模型的紧致有限差分法
(山东师范大学数学与统计学院,250358,济南)
1 引 言
本文考虑如下的Cattaneo模型:
(1)
其中Ω:={(x,t)∈R2:0≤x≤L,0 在传统的Fourier定律和Fick扩散定律描述的扩散现象中,一点在经过的一瞬时,在极远处就会受到该点的扰动影响,扰动的传播速度似乎是无限的,然而这个属性是非物理的.Cattaneo模型[1]修正了传统的Fourier定律和Fick扩散定律,通过增加一个松弛时间项来克服这个矛盾,由Christov[2]提出了Cattaneo定律的框架,并由Ostoja-Starzewski[3]给出了Maxwell-Cattaneo方程的数学推导.Haddad[4]利用Cattaneo-Christov理论研究了Brinkman多孔介质的问题,Straughan[5]研究了Cattaneo类型的不可压缩牛顿流体水平层的热对流问题.Ghazizadeh等[6]给出了分数阶Cattaneo方程的显式和隐式两种格式的有限差分算法,并且Qi等[7]给出了分数阶Cattaneo方程的精确解. 紧致有限差分法是一类高精度的有限差分方法,具有高精度、高分辨率以及对网格节点要求低等优点,受到很多学者的关注,1992年,Lele[8]提出了紧致差分格式的一般形式,Dennis和Hundson[9]研究的对流扩散方程的四阶紧致差分格式对后续研究影响较大.本文提出问题(1)的紧致差分格式,通过对具体算例进行数值模拟,并与二阶差分格式相比较,验证了其精确性和有效性. 应用公式 可得到 (2) (3) (4) (5) (6) 接下来,在此二阶差分格式的基础上建立4阶紧致差分格式,定义算子A,满足 由文献[10]中引理1.2(g),有 其中ξik∈(xi-1,xi+1) .将算子A作用于(2)式两端,并应用(3)、(4)和(5),整理可得 (7) 应用文献[10]中引理1.2(c)、(f)和(e),有 结合(1)式可得初始条件 对(7)式整理可得到 其中余项 (8) 其中紧致差分格式的截断误差为O(τ2+h4) . 在方程(1)中令ε=0.1,D=1,u0(x)=sin(πx),u1(x)=0, 由文献[11,12]可得其精确解为 对空间步长h和时间步长τ分别取对应的值,则紧致差分解与二阶差分解有以下相应的L2误差以及空间和时间收敛阶. 表1 紧致差分格式L2误差 表2 二阶差分格式L2误差 由表1、表2可以看出,紧致差分格式(8)可分别得到关于空间4阶收敛,关于时间2阶收敛,二阶差分格式(6)可得到空间、时间均为2阶收敛. 在h相同的情况下,可以明显地看出紧致差分格式(8)解的误差小于二阶差分格式(6)解的误差.由此可见,在使用同样节点数的情况下,紧致差分方法的计算精度优于二阶差分方法.2 格式建立
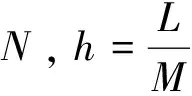
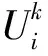
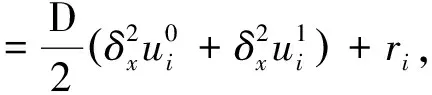
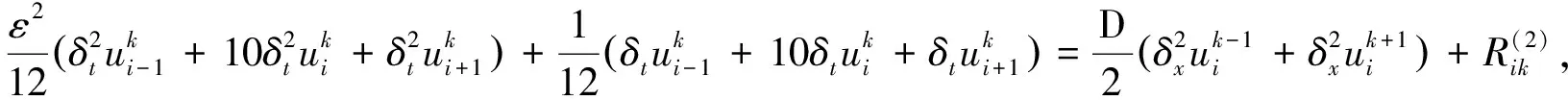
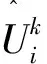
3 数值模拟