基于现代通信模型的遥远星系光色变化研究

寿元

(1) 北京师范大学天文系，100875,北京； 2) 山东师范大学信息科学与工程学院，250358,济南)

1 从现代通信模型质疑大爆炸宇宙学

光纤通信已成为现代通信的骨干网，其超长距离光孤子通信、光信号的存储、发射、信道传播、路由、接收、噪声、编码、译码、复用等技术很成熟.该文从现代通信模型重新审视遥远星系的光色变化问题.光属于电磁波范畴，它在太空遥远距离的传播过程中，应该遵循电磁波传输基本原理和通信基本模型，现代通信模型如图1所示.

图1 现代通信模型示意图

设定Xi为光源发射信号，Y0为接收端输出信号.H(y,x)为信道的传递函数，反映信道的特征.信道大部分参数与信道长度有关，信道的作用是传输信号.但是信号通过信道时有伤害、损耗、改变等.即严格意义上，输出信号不等于输入信号，一定会有所改变.n(t)-信道受外界干扰，称为干扰信号.信道传输模型如公式(1).

Y(t)=H(y,x)X(t)+n(t).

(1)

由(1)式引起对大爆炸宇宙学的质疑.

质疑1：宇宙大爆炸余辉.在(1)式中，当信号H(y,x)*X(t)小于n(t)时，接收的信号主要成分就是噪声.但是，1964年，彭齐亚斯和威尔逊在矩形号角天线上收到的3 K噪声，定义为宇宙大爆炸余辉；1989年升空COBE卫星探测到符合温度为2.726 K(误差不大于0.01 K)的黑体辐射谱的噪声，再一次认定为宇宙大爆炸余辉.噪声是通信信道的最普通的事情，到大爆炸宇宙学，噪声如何成为爆炸余辉，笔者认为有待商榷.

质疑2：信号经过信道，特别是光波在太空超长距离(几十万光年-几千万光年)的传播，地面收到的光信号的功率、振幅会有极大的衰减，信号的频带也会压缩.还产生色变、相移、失真、误码、伪信号、噪声、干扰等.但是，1929年Edwin Hubble测量到遥远星系的光色变化，频率相对衰减量与星系距离成正比的哈勃定律，沿用多普勒效应，得出宇宙膨胀、加速膨胀、大爆炸的结论[1-5].把收到光信号的频率衰减全部归结为光源的移动，太空信道没有任何影响，与现代通信原理相矛盾[6].1848年，多普勒在“论双星绕转运动的光色变化”一文中讨论双恒星由于引力绕转时，当恒星向我们方向运动时，以公转速度指向地球，光的波长会变短，出现蓝移，频率升高；当恒星运动在其轨道的另一边时，远离地球，出现红移，即频率降低.后来天文学家用该方法，测量到星系旋转运动及双恒星绕转运动方法得到验证，但是宇宙红移用多普勒效应解释，是否存在过度使用多普勒效应的问题？

质疑3：星系都远离地球，暗示地球再一次成为宇宙的中心.尽管宇宙学家一再辩解，地球不是宇宙的中心，用多维、弯曲面来诠释.但是难以消除地球成为宇宙中心的话柄.

历史的昨天：地心说与日心说争论——天旋还是地动.地球绕太阳运动容易，还是整个宇宙绕地球运动容易.伽利略说：相信哥白尼的日心说，每天看到的太阳东升西落运动都是假的，是地球运动的反映.

今天的宇宙大爆炸：整个宇宙大爆炸容易，还是光波频率衰减容易？光波频率衰减从实验上可以测量，可以通过实验来验证.宇宙大爆炸无法验证.

2 太空信道新特征—信道频率衰减

一般通信信道，主要传输各种模拟或数字信号，主要关注信号功率、振幅的衰减及噪声.对于信号的频率变化或称为色变化，因为变化极其微小，工程上影响很小，通常不考虑.

太空信道，距离超长，达几亿光年.光功率、光振幅衰减很大.天文学家把遥远星系发来的光，频率衰减即光色变红的现象，用多普勒效应解释，推理出遥远星系都后退，导致宇宙膨胀、宇宙大爆炸等结论.影响之大，震撼之深,已成为人类关注的焦点.

信道特征：任何波(包括机械波、声波、电磁波)在信道传输过程中，由于波能量存在三种主要耗散模式：第一是扩散,波能量企图占据更大的空间，使波能量密度降低；第二色散，波能在时间上企图占据更长的时间段，使波能量密度降低；第三损耗，媒质直接接触损耗或间接损耗，使波能量密度降低.波能量耗散理论分析如下：

波动是振动状态相位的传播.振源的能量以波速向外传递.假定介质中每个质量元彼此通过弹性力相联系，沿Y轴方向振动，沿X轴向传播.

波函数的一般表达式为

y(x,t)=A(x)cos(ω(x)t-kx).

(2)

式(2)中，A(x)-波的振幅，通常随传播距离而衰减，是传播距离x的函数；ω(x)——角速度.

波函数中每个质点沿Y方向振动的速度为

(3)

波函数在一个微小线元段，单位质量的动能函数Φy(x,t)为

(4)

(4)式表明波动能函数与波频率平方成正比,与波振幅平方成正比.

在一个波长范围内对фy(x,t)取均值，因为A(x)，ω(x)在一个波长范围内变化很小，认为是暂稳态值.均值只是对sin2(ω(x)t-kx)进行，得

考虑到振动的势能能量部分，则波动总能量函数φy(x,t)的均值为

(5)

(5)式表明，波能量函数与其振幅平方成正比,也与频率平方成正比.

2.1波能量随传播距离的衰减假定波函数在信道媒质内传播的功率与能量函数成正比.在一般的条件下，功率P随传播信道距离x而变化，可表示为

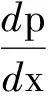
(6)

(6)式中，α是损耗系数，p(0)为信道入射端x=0处入射功率,p(x)为信道X处输出功率.

根据上面的假定，波函数在信道里传输，其能量函数受损耗的影响而衰减，α是损耗系数，设长度为X信道媒质，入射端x0振动能量函数为Φy(x0)，根据式(6)式，输出端x振动能量函数为Φy(x).

(7)

把(5)式带入(7)式，得

A2(x)ω2(x)=A2(0)ω2(0)e-αx.

(8)

两边开方，得

(9)

对(9)式进行讨论:

(10)

其振幅A(x)随传播距离x按(10)式衰减.雷同于调幅广播信号形态.

(11)

其波函数频率ω(x)随距离x按(11)式衰减.

雷同于调频广播信号传输.频率降低，波长变长，形成信道频率衰减.

3)A(x)，ω(x)共同分担信号的衰减量：

(12)

则波函数随传播距离的表达式为

(13)

振幅、频率随传播距离都衰减，衰减的份额相同.波函数随传播距离按(13)式变化.

(14)

4) 若信号频率按(14)式快速衰减，信号的能量积累到振幅上.则有A(x)>A(0).

5) 更一般自然现象，振幅A(x)随传播距离x而快速衰减，被实验和工程早已证实.但是迄今人类没有发现ω(x)随信道距离有明显的变化.由此猜想：波的衰减分成三段：1) 波能量密度很大，以传播距离、振幅衰减为主，频率衰减为辅——称为波状态；2) 波能量密度小，振幅衰减，频率衰减；3) 波能量密度非常小，振幅、频率都快速衰减为零——波消亡态.

2.2声波频率衰减的实验测量声波频率随传播距离有缓慢衰减的实验：声源→声道传播→(远传声波传感器)接收→放大处理→二次声源→声道传播→(远传声波传感器)接收→放大处理.实验测量框图如图2所示.

输入端信号频率为fi，经过信道传输后，接收端输出信号fo.信道对信号频率有极其缓慢的衰减，通过李萨图的变化，对频率衰减的相位角进行长时间的积累，可以反应出f0变化.如下式：

θ=2πtΔf=2πt(fi-f0).

(15)

(15)式中，t-时间段，可以是几个小时，也可以更长.可以实现频率衰减的极高精度的测量.

声波频率衰减实验数据：

用高灵敏度、远距离声压传感器测量到声波频率随传播距离微小衰减的结果，得到不同声音频率、不同声源功率的一系列实验数据.如用1 000 Hz声波源，100瓦扬声器，声波在山东师范大学长清校区信息楼五层120 m长廊中传播，每隔10 m设一个测量点，在100 m处频率衰减达0.1 Hz/S的衰减量.对应点的振幅衰减达1 000多倍.频率的测量数据、波长变化量、频率相对衰减量换算数据如表1所示.

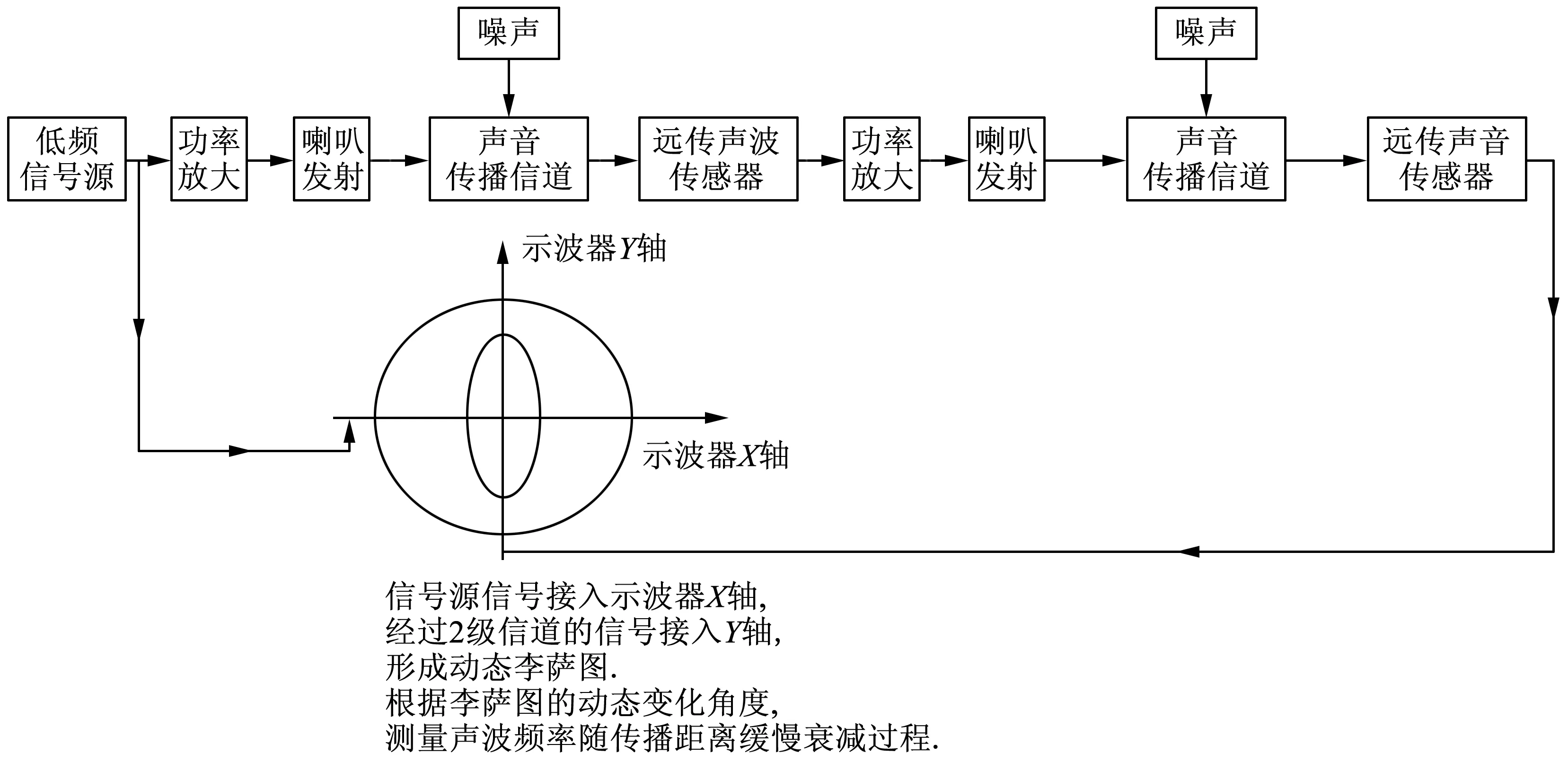
图2 声波频率随传播距离缓慢衰减的实验框图

传播距离(m)102030405060708090100频率衰减量(Hz/min)1/141/81/221.822.55.05.56.0波长增加量(μm)0.4040.7082.8311.32410.1911.3214.1528.3131.1433.97频率相对衰减量Z(10-6)1.192.088.2232.829.9732.241.082.2591.598.4

表1的实验数据表明了声波波长相对增加量(即频率相对衰减量)随距离的变化关系，数据受长廊形状、楼梯影响，在30～40 m处有楼梯、小方厅波能量扩散损耗大.

当距离不变(L=20 m)，源功率不变(P=80 db);波长变化、频率衰减、波长相对变化量随源频率变化时，测量数据如表2所示.

表2 声波频率相对衰减量随声源频率变化的实验测量

从表2实测数据可以看出，频率在高频率段相对衰减量小，低频率段相对衰减量大.频率相对衰减量大(既波长相对变化量)，损失波能量就多，与实验原理一致.

频率相对衰减量随波源功率的变化：取 距离为10 m，源频率为1 080 Hz/s.

表3 声波频率相对衰减量随声源功率变化的实验测量

从表3实验数据可以看出，声源功率较小时，频率衰减大.测量结果与实验原理吻合.

声波频率相对衰减量的三组实验表明，频率相对衰减量与传播距离、信号源功率、信号频率都有关系.从能量耗散角度更容易解释.

实验结果也与人们对声音传播的自然认识一致，如声源功率大，传播距离就远.同样音量，音调高的声音传播距离大.如放羊的牧民、大山的居民，嗓音比较高.同样的声功率，音调高，传的远，对方听得见.

2.3电磁波频率随传播距离的衰减假如电磁波是正弦平面波

H(z,t)=Hy(z)cos(ω(z)t-kz),

(16)

E(z,t)=Ex(z)cos(ω(z)t-kz).

根据麦克斯韦方程微分形式(或法拉第电磁感应定律),

(17)

电场的旋度就是矢性电位面密度,则有

V(z,t)=

(18)

电功率等于电压与电流的乘积，可以描述成电压的平方除以负载,电功率平均值,则有

(19)

在无导电媒质中，电场与磁场的关系为

矢性磁位为

A(z,t)=×B=μ

(20)

(18)式和(20)式表明，电磁波能量函数均值与振幅平方成正比，也与频率平方成正比.其能量函数、振幅、频率随传播距离衰减(分析与前面机械波雷同，不再赘述).

电磁波频率衰减的实验：信号源采用的频率从10 MHz到20 MHz范围，电磁波经过20 km的75-5同轴电缆传播，中间加20级中继放大，把电磁波源信号接到示波器X轴，经过20 km信道传播后，接Y轴.在示波器上显示李萨图，通过李萨图图形缓慢变化，换算出电磁波在信道传播后的频率衰减结果.实验框图如图3所示.

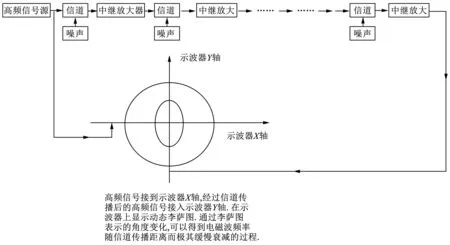
图3 电磁波频率随传播距离极其缓慢衰减的实验框图

实验结果的预估，由哈勃系数得到：每米太空信道，频率相对衰减量约为10-26/m.s.若采用光信号频率为1015Hz/s.信道长度20 km,李萨图显示角度为1 Hz=360°.1 d就是86 400 s.计算频率衰减预估结果：1 d时间内，有6°的相位角积累.这一预测结果由目前实验手段可以测量到.

如果信道输入端信号频率为fi，经过信道传输后，接收端输出信号为f0.信道对信号频率有极其缓慢的衰减.通过李萨图的变化，对频率衰减的相位角进行长时间的积累，可以反应出来f0变化.如下式：

θ=2πtΔf=2πt(fi-f0),

式中，t-时间段，可以是几个小时，也可以更长.可以实现频率衰减的极高精度的测量.

电磁波信号源fi=15 MHz，信道长度为20 km.

(21)

测量结果：频率相对衰减量除以信道长度，得到每米信道长度频率的相对衰减量，约为10-17～10-18/m.s.实验结果与预估值要大.因为地面实验室媒质物质密度比太空大得多.造成频率衰减比太空大，也是可以理解.

电磁波频率衰减实验数据：

试验频率：电磁波频率15 MHz/s.L=10 000 m.

表4 电磁波频率相对衰减量实验

观测图形椭圆的长轴与短轴的比值及图形转动，经过分析得倾角的变化值.

实验图形分转动区：45～90；90～125度；225～270度；227～215度.图形非旋转区，图形椭圆率变化区：0～45度，125～180度，180～225度；215～260度.由观测图形分析表得：图形的角度没有明显的转动变化，离散性不大.但是椭圆的长轴与短轴的比值，逐渐减小，说明图形处在215～260度之间.每天约有1度的增加.假如初始相位角为220度，运行时间为24 h，相位角222度，运行7天后，相位角累积为244度.即15兆赫兹的电磁波传播10 000 m的距离后，频率有非常微弱的减小，约为10-7Hz/S.这个试验数值与哈勃关系式预估(天文观测值)大几个量级.表4实验值与预估值基本吻合，与实验原理一致.实验结果、图形形状没有明显的变化，但是图形转动每天有1 度的旋转.

试验结果：电磁波经过20 000 m距离的传输，频率衰减，引起波长增长，每米频率相对衰减量为3.215×10-18m/s

2.4星光频率随传播距离衰减分析如果恒星亮度为L，光波以球面波的形式沿半径R向外传播，光能密度沿R距离成平方反比衰减，考虑到平面波衰减系数α，能量函数Φ，则有

(22)

振幅、信道频率相对衰减量分析雷同于2.1节(略)，则有

(23)

(23)式中,αa,αω分别是平面电磁波的振幅、频率随传播距离的衰减系数，与能量函数的衰减系数的关系：

电磁场、电磁波的磁场强度表达式为

(24)

(电场强度表达式磁场强度雷同,略)

3 星系视向运动与光色变化

若光传播路途频率损耗系数为定值α，恒星发射光波长为λs,观测点光的波长为λo，恒星到地球的距离为D，则有

λ0=λsead.

(25)

产生的频率相对衰减量(波长相对变化量)为

由于频率随传播距离非常小的衰减，当距离已经很大，几十光年、甚至几百万光年，频率相对衰减量仍然很小时，上式进行一级近似，得

z=ad.

(26)

(26)式与1929年Edwin Hubble测量到遥远星系的光色变化，波长相对变化量——红移，即频率相对衰减量与星系距离成正比的哈勃定律、理论分析与实测完全一致.只是命名有所不同，前者的比例系数叫做信道频率衰减系数，哈勃公式称为哈勃系数，哈勃系数缺乏深层的物理含义.

(27)

恒星或星系与地球的距离确实存在视向运动，有的远离，有的接近.这个用波源移动的多普勒效应来处理是恰当的.

多普勒效应：光源移动的视向速度v，接近观测点，波长变短，频率升高-产生蓝移.如果光源以速度v远离观测者，则频率降低，波长变长，形成所谓的红移.

基于光源移动，对于观测者形成的光色变化，如图4所示.多普勒效应与信号源距离没有任何关系，或者说光源移动引起的光色变化：频率相对变化量，红移或者蓝移，仅与光源移动的速度大小成比例、与光源移动方向决定光色变化正负号.

(28)

星光信道频率相对衰减量：星光传播途径、距离，决定光波频率的衰减量.光色频率相对衰减量与距离成指数关系，只有红移，没有蓝移.如图5所示.

综合光源移动的多普勒效应，信道频率相对衰减量效应(注：波在传播过程中，存在扩散、色散和损耗等作用，致使信号频率随传播距离有极其缓慢的衰减)后.星光光色变化分三种情况来讨论：

1) 离地球近的恒星或星系，信道频率相对衰减量小：A) 如果恒星光源快速向地球移动，多普勒效应的蓝移大于信道产生的频率相对衰减量，综合后呈现蓝移；B) 如果恒星远离地球，这类恒星发来的光，由于光源移动产生频率衰减与信道频率衰减量作用一致，测量到的频率相对衰减量是两者之和.多普勒效应起主要作用；C) 如果恒星与地球距离没有变化，多普勒效应为零，仅有光信号传播引起频率衰减，造成的信道频率相对衰减量很微弱.

图4 光源移动对于观测者来说：光色变化

图5 信道频率相对衰减量与距离成指数关系

2) 如果距离满足信道频率相对衰减量与光源移动蓝移抵消的距离点，光色没有变化；有信道频率相对衰减量与多普勒效应蓝移量，相加等于零，如下式所示.

(29)

星系接近地球运动的速度与星系距离满足的条件，地球观测者对该类星系光色的测量值没有变化.

3) 随着离地球的距离增加，距离产生的信道频率相对衰减量也随之增加，导致信道频率相对衰减量大于光源移动蓝移的恒星个数增加.总的结果是频率相对衰减量导致红移的星系个数多于蓝移的个数.如果距离大于信道频率相对衰减量与光源移动蓝移抵消的距离点，那么，地球测量到星系发来的光全是红移.

(30)

4) 更遥远的星系：星光色变化以信道频率衰减为主，以多普勒效应为辅.地球接收到的遥远星系的光色全部变红(即频率相对衰减量).

4 星光色变结论

多普勒蓝移(频率相对增加量)仅与光源接近运动速度成比例；多普勒红移(频率相对减少量)仅与光源远离时运动速度成比例，与距离远近无关.哈勃测量到频率相对衰减量与距离成正比例关系，与信道频率相对衰减量特征高度一致.