退化量子群Uq(sl2,1)
(1) 山东师范大学数学与统计学院,250358,济南; 2) 悉尼大学数学与统计学院,2006,悉尼)
1 引 言
量子群[1,2]于80年代中期产生于统计力学中Yang-Baxter类型的可积模型理论.之后,对这些代数结构的研究取得广泛的成果并发展成为一个巨大研究领域[3,4].量子群理论在数学物理和纯数学中的许多领域都有重要应用,例如:可积模型,共形场论,低维拓扑[5-7]和表示理论[4]等.本文中我们提出了量子群Uq(sl3)的退化形式Uq(sl2,1),并详细研究了它的Hopf代数结构和有限维表示.
2 退化量子群Uq(sl2,1)的定义
我们知道Uq(sl3)由两个Uq(sl2)子代数生成.这两个子代数被特定的关系联系起来,如Serre 关系.相应的退化量子群Uq(sl2,1)保持其中一个Uq(sl2)子代数不变,另一个退化成Zachos’代数,其中Zachos’代数[8]由k,k-1,X+,X-生成,这些元素满足如下关系:
kk-1=1,kX±k-1=-X±,
我们给出退化量子群Uq(sl2,1)的定义.
定义1Uq(sl2,1)是定义在C(q)上的含幺结合代数,由ei,fi,ki,ki-1(i=1,2)生成,且它们之间满足如下关系:
kiki-1=1,ki±1kj±1=kj±1ki±1, ∀i,j,
(1)
kiejki-1=q-1ej,kifjki-1=qfj,i≠j,
(2)
k1e1k1-1=q2e1,k1f1k1-1=q-2f1,
(3)
k2e2k2-1=-e2,k2f2k2-1=-f2,
(4)
(5)
e12e2-(q+q-1)e1e2e1+e2e12=0,
(6)
f12f2-(q+q-1)f1f2f1+f2f12=0,
(7)
e22=0,f22=0,
(8)
称Uq(sl2,1)为sl3的退化量子群.
注1 元素k2±1,e2,f2生成的子代数同构与Zachos’代数,即退化的量子sl2,可记作Uq(sl1,1).
注2Uq(sl2,1)不同于量子超群Uq(sl2|1)在于(4),(5)两式.若将(4),(5)两式各换为下面的关系式:
其中[e1]=[f1]=0,[e2]=[f2]=1是这些元素的奇偶性,则得到量子超群Uq(sl2|1),且Uq(sl2|1)具有Hopf超代数结构,之后将会看到Uq(sl2,1)有Hopf代数结构.

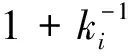


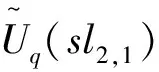
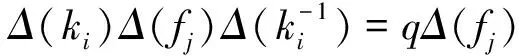
因此,Δ为同态,且需证Δ为余结合的,我们只需在生成元处证明满足即可,如:
其他几个生成元的证明类似.

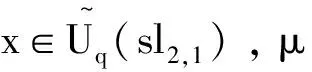
下证S为代数反自同构,如证明(5)式,
S(eifj-fjei) =S(fj)S(ei)-S(ei)S(fj)
μ(S⊗id)Δ(x)=μ(id⊗S)Δ(x)=ε(x).
(9)

则有下面的等式成立,
(10)
(11)
(12)

(13)
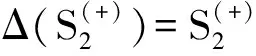
(14)

(15)
(16)






∀i.(11)式得证.
Δ(e12e2)=e12e2⊗k12k2+q-2e12⊗e2k12+(1+q2)e1e2⊗e1k1k2
+(q+q-1)e1⊗e1e2k1+e2⊗e12k2+1⊗e12e2,
Δ(e2e12)=e2e12⊗k12k2+(q+q-1)e2e1⊗e1k1k2+q-2e2⊗e12k2
+e12⊗e2k12+(1+q2)e1⊗e2e1k1+1⊗e2e12,
因此我们得到,
Δ(e12e2)+Δ(e2e12)=(e12e2+e2e12)⊗k12k2+1⊗(e12e2+e2e12)+(q+q-1)W,
其中,W=e2e1⊗e1k1k2+e1⊗e1e2k1+q-1e2⊗e12k2+qe1⊗e2e1k1+q-1e12⊗e2k12+qe1e2⊗e1k1k2,
Δ(e1e2e1)=e1e2e1⊗k12k2+1⊗e1e2e1+W.因此,
(13)式证明类似,下证(14)式,
(15)式的证明与(14)式的证明类似不再赘述. (16)式中的关系式是显然的,证毕.
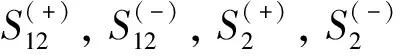
证由引理2显然得到此定理, 证毕.
3 Uq(sl2,1)的一些结构性质
下面我们研究Uq(sl2,1)的结构.由Uq(sl2,1)的定义知{e1,e2},{f1,f2},{k1±1,k2±1}三个集合分别生成三个子代数U+,U-,U0.并且{e1,e2}∪{k1±1,k2±1}也生成一个子代数,记为Uq(b).
引理3 代数Uq(sl2,1)满足三角分解Uq(sl2,1)=U-U0U+,即Uq(sl2,1)中的每个元素都可以表示成形如u-u0u+的线性组合,其中u-∈U-,u0∈U0,u+∈U+.进一步,Uq(b)=U0U+.
证由Uq(sl2,1)的定义可知,总能把ki移到ei的左边,把fi移到ei左边,再移到ki的左边,i=1,2.因此引理显然成立,证毕.
下面的引理4和5为Uq(sl2,1)的表示做准备.
引理4 令F:=f1f2-qf2f1,则下面的几个等式成立,
f1F=q-1Ff1,f2F=-q-1Ff2,F2=0,
(17)
e1F-Fe1=f2k1-1,e2F-Fe2=-qf1k2,
(18)
f1kf2=[k]qFf1k-1+qkf2f1k.
(19)
证由f1与f2之间的Serre关系,f1F=f12f2-qf1f2f1=q-1f1f2f1-f2f12=q-1Ff1. 由f22=0,f2F=f2(f1f2-qf2f1)=f2f1f2=-q-1(f1f2-qf2f1)f2=-q-1Ff2.因此F2=(f1f2-qf2f1)F=-q-2F(f1f2-qf2f1)=-q-2F2,所以F2=0,(17)式得证.
记[x,y]=xy-yx,∀x∈Uq(sl2,1),则有
[e2,F]=f1[e2,f2]-q[e2,f2]f1
=-qf1k2,
e1F-Fe1=f2k1-1可用同样的方法证明,此处省略.(18)式得证.
k=0,1时,(19)式显然成立,设k时,(19)式成立,下证k=k+1时(19)式成立,
f1k+1f2=([k]qq-1+qk)Ff1k+qk+1f2f1k+1=[k+1]qFf1k+qk+1f2f1k+1,
证毕.
由引理3和引理4,我们能得到U-的PBW基.
引理5 集合{f1k,f2f1k,Ff1k,Ff2f1k|k=0,1...}为U-的一个基,称它为一个PBW基.
证先证此集合生成U-,因为f22=0,则U-由下面形式的元素生成,
f1j1f2f1j2f2f1j3...f1jr-1f2f1jr,j1,j2,...,jr∈Z+,0 其中若r=1,元素为f1j1.下证f2f1if2f1jf2=0,∀i,j≥0.i=0或j=0时,显然成立. 设i,j>0,由引理4中的(19)式得, f2f1if2f1jf2=[j]qf2f1if2Ff1j-1 =[j]q[i]qf2Ff1i-1Ff1j-1 =[j]q[i]qqi-1f2FFf1i+j-2 =0, 因此,在(20)式中,r≤3,即U-由f1j1,f1j1f2f1j2,f1j1f2f1j2f2f1j3生成. 设引理中的集合生成的代数记为U′,则U′为U-的子代数显然,下证U-⊆U′,其中f1j1,f1j1f2f1j2∈U′显然,f1j1f2f1j2f2f1j3=-q2j1+1[j2]qFf2f1j1+j2+j3-1∈U′,所以U-⊆U′,即U′=U-. 下证集合{f1k,f2f1k,Ff1k,Ff2f1k|k=0,1...}中的元素线性无关.考虑单Uq(sl2,1)最高权模L(λ),λ=(λ1,λ2)=(q-2,q-1),则L(λ)由下面的元素生成, f1kvλ,f2f1kvλ,Ff1kvλ,Ff2f1kvλ,k∈Z+. (21) 下证这些元素线性无关. 可以看到(21)式中的元素同为k1,k2的特征向量,因为属于同一线性变换的不同特征值的向量线性无关,因此我们仅需考虑相同特征值的特征空间.取(21)式中k1,k2的公共特征空间中元素的任意非平凡的线性组合,若值等于为0,则左边同时乘以f2,F或f2F,则得到对于某一k0,Ff2f1k0vλ=0,且我们知 e2Ee1k0Ff2f1k0vλ=(q+q-1)avλ≠0,则与Ff2f1k0vλ=0矛盾,所以(21)式中的向量线性无关,证毕. 由引理3知Uq(sl2,1)存在三角分解,则我们可以构造Uq(sl2,1)的最高权模. 给定一λ:=(λ1,λ2),0≠λi∈C(q),设C(q)vλ为Uq(b)-模,基为vλ,且有eivλ=0, kivλ=λivλ,i=1,2.我们称vλ是权为λ的最高权向量.则V(λ):=Uq(sl2,1)⊗Uq(b)C(q)vλ在自然的左作用下成为Uq(sl2,1)-模,类似于李代数的Verma模,作为向量空间 V(λ)=U-⊗C(q)vλ, (22) 可以看到V(λ)包含唯一的极大子模M(λ),M(λ)为不包含最高权向量1⊗Vλ的子模的直和. 令L(λ):=V(λ)/M(λ),则L(λ)为V(λ)的单商模.为简单起见,我们将V(λ)中的元素u⊗vλ在L(λ)中的像记为uvλ,其中u∈Uq(sl2,1). 引理6 设L(λ)为单Uq(sl2,1)-模,其中λ=(λ1,λ2)为最高权,L(λ)为有限维模当且仅当 λ1=±ql,l∈Z+. 证S由e1,f1,k1±1生成的Uq(sl2)为Uq(sl2,1)的子代数,则可知L(λ)同样也为Uq(sl2,1)-模,则由Uq(sl2,1)-模为有限维知λ1=±ql,l∈Z+,必要性得证. 下证充分性,现假设λ1=±ql,对某一固定的l∈Z+,设L0(λ)为L(λ)的子空间,基为B0={ f1kvλ|k=0,1,2,...,l}.由Uq(sl2)的表示理论知B0中的元素线性无关,L0(λ)为Uq(sl2)的子模.更多的,B0中的元素为k1,k2的公共特征向量,由(5)式知,e2f1kvλ=0,k=0,1,2,...,l成立,则e2v=0,∀v∈L0(λ),则uv∈L0(λ),∀v∈L0(λ),u∈U0U+.因为L0(λ)包含最高权向量,它生成了L(λ),则由引理3和式(22),L(λ)=U-vλ.由引理5知,L(λ)由下面的向量张成, f1kvλ,f2f1kvλ,Ff1kvλ,Ff2f1kvλ,k=0,1,...,l. (23) 则可知dimL(λ)≤4(l+1),因此为有限维的,充分性得证,证毕. 定理2 设λ=(λ1,λ2),其中λ1=±ql,l为一非负整数,则单Uq(sl2,1)-模L(λ)的维数为4(l+1)当且仅当(qλ1λ2-q-1λ1-1λ2-1)(λ2-λ2-1)≠0,且(21)式中的向量为L(λ)的基. 证容易看出dimL(λ)<4(l+1)当且仅当(21)式中的向量线性相关,因此存在(21)式中的向量做非平凡的线性结合等于0,由于f22=0,f2F=-q-1Ff2以及F2=0,则用f2,F或f2F乘到等式的左边,得到对于某一非负整数k0≤l,Ff2f1k0vλ=0. 由引理5的证明过程我们知道e1k0Ff2f1k0vλ=Ff2e1k0f1k0vλ,且有e1k0f1k0vλ=ck0vλ,其中 因此e1k0Ff2f1k0vλ=ck0Ff2vλ=0,即Ff2vλ=0,其为dimL(λ)<4(l+1)的充分必要条件. 此式成立当且仅当下式成立, 由上式知,要使得dimL(λ)<4(l+1),其充分必要条件为下式成立, (qλ1λ2-q-1λ1-1λ2-1)(λ2-λ2-1)=0. (24) 定理的第一部分得证,第二部分由第一部分显然成立,证毕. 定理3 设λ1=±ql,l∈Z+,式(24)成立,则λ2取值为±1或±q-1λ1-1. 若λ2取值为±1,则L(λ)维数为2l+1,基为 {f1jvλ,Ff1kvλ|0≤j≤l,0≤k≤l-1}. (25) 若λ2取值为±q-1λ1-1,则L(λ)维数为2(l+1)+1,基为 {f1kvλ,f2f1kvλ,Ff1lvλ|0≤k≤l}. (26) 证由(24)式,定理的第一部分显然成立,由定理2知,∀k≥0,Ff2f1kvλ=0.我们需要考查Ff1kvλ与f2f1kvλ的线性相关性,当λ2=±1时,我们有f2vλ=0,则f1f2vλ=Fvλ+qf2f1vλ=0,即Fvλ=-qf2f1vλ.更多的,由f1Ff1k-1=q-1Ff1k,f1f2f1k=Ff1k+qf2f1k+1,以及对k进行归纳可得到, 因此(25)式生成L(λ). 若假设l=0,则f1vλ=0,Fvλ=0.若l>0,则 e1Fvλ=-qf2e1f1vλ=0.更多的,k1Fvλ=±ql-1Fvλ,因此Fvλ是子代数Uq(sl2)的权为±ql-1的最高权向量,则Fvλ生成l维的Uq(sl2)-子模,基向量为Ff1kvλ,k=0,1,...,l-1.令B1:={Ff1kvλ|0≤k≤l-1},则可知B1中的向量线性无关.B0:={f1kvλ|0≤k≤l}中的向量也线性无关,B1中的向量在k2下所对应的特征值为B0/{vλ}中向量在k2下所对应特征值的负值,则这两个向量集线性无关,因此(25)式为L(λ)的一组基. 当λ2=±q-1λ1-1,若l=0,易得{vλ,f2vλ,Fvλ=f1f2vλ}为L(λ)的一组基.若l>0,由关系式e2Ff2vλ=0得[l]qFvλ=q-lf2f1vλ.可用归纳法证明[l-k]qFf1kvλ=qk-lf2f1k+1vλ,k=0,1,…,l-1,其中f2f1k+1vλ是非零的.特别的,当k=l-1时,Ff1l-1vλ=q-1f2f1lvλ,则Ff1lvλ=f1f2 f1lvλ.下证f1f2f1lvλ≠0. e1f1f2f1lvλ=±([l-1]qf2f1l+[l]qf1f2f1l-1)vλ =±([l-1]qf2f1l+[l]qFf1l-1+[l]qqf2f1l)vλ =±([l-1]q+(q+q-1)[l]q)f2f1lvλ≠0, 因此,(26)式中的向量非零且生成L(λ).类似λ=±1证明过程中权的分析可知,(26)式中的向量线性无关,因此为L(λ)一组基,证毕. 通过对退化量子群Uq(sl2,1)的结构以及表示理论的分析,可以看出此代数具有较好的性质以及表示,同样可将Uq(sl2,1)的定义推广到所有经典李代数的退化量子群.并对它们的结构及表示进行研究.我们希望找出Uq(sl2,1)与Uq(sl2|1)确切的联系,这样可以为研究量子超群提供一个新的方法.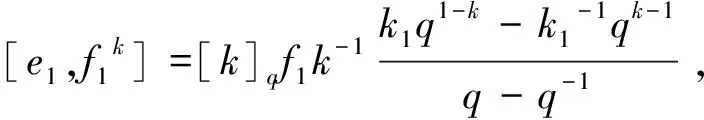
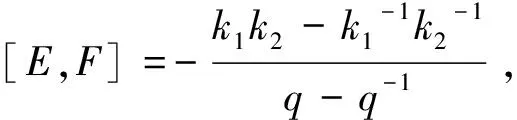
4 有限维的表示理论



5 结 语

