LR-C-good B-quasi-Ehresmann半群

(山东师范大学数学与统计学院，250358，济南)

Abstract Firstly,we define the LR-C-good B-quasi-Ehresmann semigroups.Secondly,we study the structures of LR-C-good B-quasi-Ehresmann semigroups.Finally,we get the structure theorem of LR-C-good B-quasi-Ehresmann semigroups.

Key words B-semiabundant semigroups； C-good B-quasi-Ehresmann semigroups； LR-C-good B-quasi-Ehresmann semigroups； LR-regular band

1 引言及预备知识

众所周知，广义正则半群的研究在半群代数理论中占有重要的地位,利用各种广义格林关系可定义和研究一些广义正则半群[1-3].本文利用广义格林关系来研究LR-C-good B-quasi-Ehresmann半群.

设S为半群,S中的所有幂等元集合记为E(S).S中的所有二元关系形成的格,所有等价关系形成的格,所有左同余形成的格,所由右同余形成的格和所有同余形成的格分别记为Β(S),ε(S),LC(S),RC(S)和C(S).

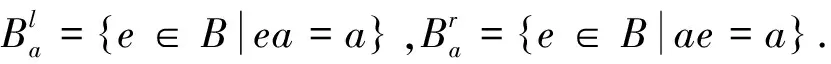
设S为半群,E(S)是S的幂等元集合且B⊆E(S),在S上的格林关系为

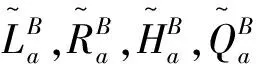
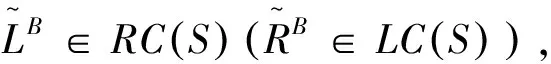
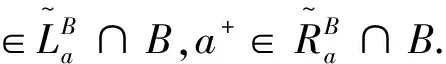
注1 若S是一个满足(C)的B-半富足半群且B是S的子半格,则称S为Ehresmann半群.

注2 设S为B-quasi-Ehresmann半群,若B是S的子半格,则称S为Ehresmann半群.

定义B-quasi-Ehresmann半群S上的等价关系γ为

(∀a,b∈S)(a,b)∈γ⟺γa=γb⟺B(a+)aB(a*)=B(b+)bB(b*).

定义3[3]设S为B-quasi-Ehresmann半群,若

(∀a,b∈S)aB(a*)B(b+)b⊆γab,

则称S为good B-quasi-Ehresmann半群；若B是S的中心,则称S为C-good B-quasi-Ehresmann半群.

定义5[2]设S为B-丰富半群,若B是S的子半群,∀a,b∈S,

aB(a*)B(b+)b⊆γab；

且

(∀e∈B)eS⊆Se.

其中D(B)={(e,f)∈B×B|(∃g∈B)eRgLf},则称S为左C-good B-quasi-Ehresmann半群.

定义6[4]设S为B-丰富半群且

其中D(B)={(e,f)∈B×B|(∃g∈B)eRgLf},则称S为纯整B-丰富半群.

引理1[5]设B是一个带,则

(i)B是左正则带⟺∀e,f∈B,efe=ef;

(ii)B是右正则带⟺∀e,f∈B,efe=fe;

(iii)B是正则带⟺∀e,f,g∈B,efege=efge.

定义7 设S为纯整B-丰富半群,若B是一个正则带,且

(∀a,b∈S)aB(a*)B(b+)b⊆γab,

则称S为拟-C-good B-quasi-Ehresmann半群.

定义8 设E是一个带,若

(∀e∈E)[(∀f∈E)efe=fe,(∀f∈E)efe=ef],

则称E为LR-正则带.

定义9 设S为纯整B-丰富半群,若B是一个LR-正则带,且

(∀a,b∈S)aB(a*)B(b+)b⊆γab,

则称S为LR-C-good B-quasi-Ehresmann半群.显然,一个LR-C-good B-quasi-Ehresmann半群是一个拟-C-good B-quasi-Ehresmann半群.

本文中用Τl(X)和Τr(X)分别表示集合X上的左变换半群和右变换半群.

引理3[7]设T=[Y;Tα]是一个C-good B-quasi-Ehresmann半群,I=[Y;Iα]是一个左正则带且Λ=[Y;Λα]是一个右正则带.若映射

满足下列条件：

(L1) 若(i,x)∈Iα×Tα且j∈Iβ,则(i,x)#j∈Iαβ；

(R1) 若(x,λ)∈Tα×Λα且μ∈Λβ,则μ(x,λ)*∈Λαβ；

(L2) 在(L1)中,若α≤β,则(i,x)#j=i；

(R2) 在(R1)中,若α≤β,则μ(x,λ)*=λ；

(L3) 若(i,x)∈Iα×Tα且(j,y)∈Iβ×Tβ,则(i,x)#(j,y)#=((i,x)#j,xy)#；

(R3) 若(x,λ)∈Tα×Λα且(y,μ)∈Tβ×Λβ则(x,λ)*(y,μ)*=(xy,λ(y,μ)*)*；

则S(B)=∪α∈Y(Iα×Tα×Λα)关于二元运算

(i,x,λ)(j,y,μ)=((i,x)#j,xy,λ(y,μ)*)

构成一个拟-C-good B-quasi-Ehresmann半群.

反之,每个拟-C-good B-quasi-Ehresmann半群都可如此构造.

引理4[7]设T=[Y;Tα]是一个C-good B-quasi-Ehresmann半群,对于∀α∈Y,Iα和Λα是两个非空集合且Iα∩Iβ=∅=Λα∩Λβ(α≠β).作直积Pα=Iα×Tα和Qα=Tα×Λα(α∈Y).记S=∪α∈Y(Iα×Tα×Λα)且B=∪α∈Y(Iα×{1Tα}×Λα).对∀α,γ∈Y,γ≤α时,设映射

满足下列条件：

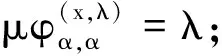
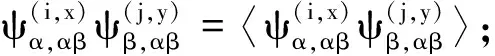
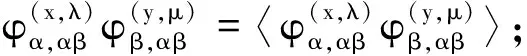
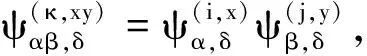
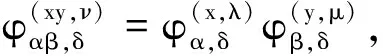
则S(B)=∪α∈Y(Iα×Tα×Λα)关于二元运算

构成一个拟-C-good B-quasi-Ehresmann半群,其中B=∪α∈Y(Iα×{1Tα}×Λα).

反之,每个拟-C-good B-quasi-Ehresmann半群都可如此构造.

2 LR-C-good B-quasi-Ehresmann半群

本节主要研究LR-C-good B-quasi-Ehresmann半群,得到了LR-C-good B-quasi-Ehresmann半群的结构定理.

B(S)⊆(C(B(S1))×B(S2))∪(B(S1)×C(B(S2))).

其中B(S)=∪α∈Y((Iα×{1Tα})×({1Tα}×Λα)),B(S1)=∪α∈Y(Iα×{1Tα}),B(S2)=∪α∈Y({1Tα}×Λα)且C(B(Si))是B(Si)的中心,i=1,2.

下证B(S)⊆(C(B(S1))×B(S2))∪(B(S1)×C(B(S2))).

设e=((i,1Tα),(1Tα,λ)),下面分两种情况证明.

1) 若∀f∈B(S),efe=ef,则证(1Tα,λ)∈C(B(S2)).

∀(1Tβ,μ)∈B(S2),则∃(j,1Tβ)∈B(S1),使得((j,1Tβ),(1Tβ,μ))∈B(S).因此

efe=ef⇒((i,1Tα),(1Tα,λ))((j,1Tβ),(1Tβ,μ))=((i,1Tα),(1Tα,λ))((j,1Tβ),(1Tβ,μ))

⇒((i,1Tα)(j,1Tβ)(i,1Tα),(1Tα,λ)(1Tβ,μ)(1Tα,λ))=((i,1Tα)(j,1Tβ),(1Tα,λ)(1Tβ,μ))

⇒((i,1Tα)(j,1Tβ),(1Tβ,μ)(1Tα,λ))=((i,1Tα)(j,1Tβ),(1Tα,λ)(1Tβ,μ))

⇒(1Tβ,μ)(1Tα,λ)=(1Tα,λ)(1Tβ,μ),

所以(1Tα,λ)∈C(B(S2)).

2) 若∀f∈B(S),efe=fe,则证(i,1Tα)∈C(B(S1)).

∀(j,1Tβ)∈B(S1),则∃(1Tβ,μ)∈B(S2),使得((j,1Tβ),(1Tβ,μ))∈B(S).因此

efe=fe⇒((i,1Tα),(1Tα,λ))((j,1Tβ),(1Tβ,μ))=((j,1Tβ),(1Tβ,μ))((i,1Tα),(1Tα,λ))

⇒((i,1Tα)(j,1Tβ)(i,1Tα),(1Tα,λ)(1Tβ,μ)(1Tα,λ))

=((j,1Tβ)(i,1Tα),(1Tβ,μ)(1Tα,λ))

⇒((i,1Tα)(j,1Tβ),(1Tβ,μ)(1Tα,λ))

=((j,1Tβ)(i,1Tα),(1Tβ,μ)(1Tα,λ))

⇒(i,1Tα)(j,1Tβ)=(j,1Tβ)(i,1Tα),

所以(i,1Tα)∈C(B(S1)).

于是有B(S)⊆(C(B(S1))×B(S2))∪(B(S1)×C(B(S2))).

充分性.设S是一个满足假设条件的群,则将证明S是一个LR-C-good B-quasi-Ehresmann半群.由引理2知S是一个拟-C-good B-quasi-Ehresmann半群,则只需证明B(S)是一个LR-正则带.∀e=((i,1Tα),(1Tα,λ))∈B(S).下面分两种情况证明.

1) 若e∈(C(B(S1))×B(S2)),即(i,1Tα)∈C(B(S1)),则对∀f=((j,1Tβ),(1Tβ,μ))∈B(S),有

efe=((i,1Tα),(1Tα,λ))((j,1Tβ),(1Tβ,μ))((i,1Tα),(1Tα,λ))

=((i,1Tα)(j,1Tβ)(i,1Tα),(1Tα,λ)(1Tβ,μ)(1Tα,λ))

=((i,1Tα)(j,1Tβ),(1Tβ,μ)(1Tα,λ))

=((j,1Tβ)(i,1Tα),(1Tβ,μ)(1Tα,λ))

=((j,1Tβ),(1Tβ,μ))((i,1Tα),(1Tα,λ))

=fe.

2) 若e∈(B(S1)×C(B(S2))),即(1Tα,λ)∈C(B(S2)),则

对∀f=((j,1Tβ),(1Tβ,μ))∈B(S),有

efe=((i,1Tα),(1Tα,λ))((j,1Tβ),(1Tβ,μ))((i,1Tα),(1Tα,λ))

=((i,1Tα)(j,1Tβ)(i,1Tα),(1Tα,λ)(1Tβ,μ)(1Tα,λ))

=((i,1Tα)(j,1Tβ),(1Tβ,μ)(1Tα,λ))

=((i,1Tα)(j,1Tβ),(1Tα,λ)(1Tβ,μ))

=((i,1Tα),(1Tα,λ))((j,1Tβ),(1Tβ,μ))

=ef.

综上知B(S)是一个LR-正则带,所以S是一个LR-C-good B-quasi-Ehresmann半群.

定理2 设T=[Y;Tα]是一个C-good B-quasi-Ehresmann半群,I=[Y;Iα]是一个左正则带且Λ=[Y;Λα]是一个右正则带.若映射

满足下列条件：

(L1) 若(i,x)∈Iα×Tα且j∈Iβ,则(i,x)#j∈Iαβ；

(R1) 若(x,λ)∈Tα×Λα且μ∈Λβ,则μ(x,λ)*∈Λαβ；

(L2) 在(L1)中,若α≤β,则(i,x)#j=i；

(R2) 在(R1)中,若α≤β,则μ(x,λ)*=λ；

(L3) 若(i,x)∈Iα×Tα且(j,y)∈Iβ×Tβ,则(i,x)#(j,y)#=((i,x)#j,xy)#；

(R3) 若(x,λ)∈Tα×Λα且(y,μ)∈Tβ×Λβ则(x,λ)*(y,μ)*=(xy,λ(y,μ)*)*；

(P) 若i∈Iα,λ∈Λα,则∀β≤α,∀j∈Iβ,(i,1Tα)#j=j(这时根据L2)有|Iα|=1)或∀β≤α,∀μ∈Λβ,μ(1Tα,λ)*=μ(这时根据(R2)有|Λα|=1).

则S(B)=∪α∈Y(Iα×Tα×Λα)关于二元运算

(i,x,λ)(j,y,μ)=((i,x)#j,xy,λ(y,μ)*)

构成一个LR-C-good B-quasi-Ehresmann半群,其中B=∪α∈Y(Iα×{1Tα}×Λα).

反之,每个LR-C-good B-quasi-Ehresmann半群都可如此构造.

证必要性.设S是如此构造的,由引理3知S是拟-C-good B-quasi-Ehresmann半群,因此只需证明B是一个LR-正则带.

设e=(i,1Tα,λ)∈B,i∈Iα,λ∈Λα,α∈Y,下面分两种情况证明.

1) 若∀β≤α,∀j∈Iβ,(i,1Tα)#j=j,则对∀f=(κ,1Tγ,ν)∈B,有

efe=(i,1Tα,λ)(κ,1Tγ,ν)(i,1Tα,λ)

=(i,1Tα,λ)((κ,1Tγ)#i,1Tαγ,ν(1Tα,λ)*)

=((κ,1Tγ)#i,1Tαγ,ν(1Tα,λ)*)

=(κ,1Tγ,ν)(i,1Tα,λ)

=fe.

2) 若∀β≤α,∀μ∈Λβ,μ(1Tα,λ)*=μ,则对∀f=(κ,1Tγ,ν)∈B,有

efe=(i,1Tα,λ)(κ,1Tγ,ν)(i,1Tα,λ)

=((i,1Tα)#κ,1Tαγ,λ(1Tλ,ν)*)(i,1Tα,λ)

=((i,1Tα)#κ,1Tαγ,λ(1Tλ,ν)*)

=(i,1Tα,λ)(κ,1Tγ,ν)

=ef

综上知B是一个LR-正则带,故S是一个LR-C-good B-quasi-Ehresmann半群.

充分性.设S是一个LR-C-good B-quasi-Ehresmann半群,则S是一个拟-C-good B-quasi-Ehresmann半群.由引理3知S能够满足(L1)→(R3).

设e=(i,1Tα,λ)∈B,i∈Iα,λ∈Λα,下面分两种情况证明.

1) 若∀f∈B(S),efe=ef,则对∀β≤α,∀μ∈Λβ,f=(j,1Tβ,μ)∈B,有

efe=ef⇒(i,1Tα,λ)(j,1Tβ,μ)(i,1Tα,λ)=(i,1Tα,λ)(j,1Tβ,μ)

⇒((i,1Tα)#j,1Tβ,λ(1Tβ,μ)*)(i,1Tα,λ)=((i,1Tα)#j,1Tβ,λ(1Tβ,μ)*)

⇒((i,1Tα)#j,1Tβ,μ)(i,1Tα,λ)=((i,1Tα)#j,1Tβ,μ)

⇒((i,1Tα)#j,1Tβ,μ(1Tα,λ)*)=((i,1Tα)#j,1Tβ,μ).

所以有μ(1Tα,λ)*=μ.

2) 若∀f∈B(S),efe=fe,则对∀β≤α,∀j∈Iβ,f=(j,1Tβ,μ)∈B,有

efe=fe⇒(i,1Tα,λ)(j,1Tβ,μ)(i,1Tα,λ)=(j,1Tβ,μ)(i,1Tα,λ)

⇒(i,1Tα,λ)((j,1Tβ)#i,1Tβ,μ(1Tα,λ)*)=((j,1Tβ)#i,1Tβ,μ(1Tα,λ)*)

⇒(i,1Tα,λ)(j,1Tβ,μ(1Tα,λ)*)=(j,1Tβ,μ(1Tα,λ)*)

⇒((i,1Tα)#j,1Tβ,μ(1Tα,λ)*)=(j,1Tβ,μ(1Tα,λ)*),

所以有(i,1Tα)#j=j.

综上S满足条件(P),所以S能够这样构造.

定理3 设T=[Y;Tα]是一个C-good B-quasi-Ehresmann半群,对于∀α∈Y,Iα和Λα是两个非空集合且Iα∩Iβ=∅=Λα∩Λβ(α≠β).作直积Pα=Iα×Tα和Qα=Tα×Λα(α∈Y).记S=∪α∈Y(Iα×Tα×Λα)且B=∪α∈Y(Iα×{1Tα}×Λα).对∀α,γ∈Y,γ≤α时,设映射

满足下列条件：

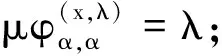
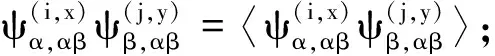
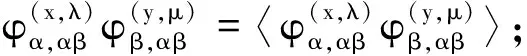
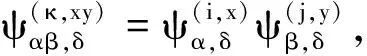
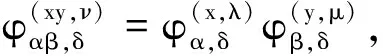
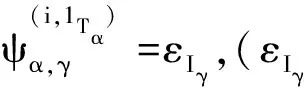
则S(B)=∪α∈Y(Iα×Tα×Λα)关于二元运算

构成一个LR-C-good B-quasi-Ehresmann半群.

反之,每个LR-C-good B-quasi-Ehresmann半群都可如此构造,B=∪α∈Y(Iα×{1Tα}×Λα).

证必要性.设S是如此构造的,由引理4知S是拟-C-good B-quasi-Ehresmann半群,因此只需证明B是一个LR-正则带.

设e=(i,1Tα,λ)∈B,i∈Iα,λ∈Λα,α∈Y,下面分两种情况证明.

efe=(i,1Tα,λ)(j,1Tβ,μ)(i,1Tα,λ)

=(j,1Tβ,μ)(i,1Tα,λ)

=fe.

2) 若∀γ≤α,φ(1Tα,λ)α,γ=εΛγ,则对∀f=(j,1Tβ,μ)∈B,有

efe=(i,1Tα,λ)(j,1Tβ,μ)(i,1Tα,λ)

=(i,1Tα,λ)(j,1Tβ,μ)

=ef.

综上知B是一个LR-正则带,故S是一个LR-C-good B-quasi-Ehresmann半群.

充分性.设S是一个LR-C-good B-quasi-Ehresmann半群,则S是一个拟-C-good B-quasi-Ehresmann半群.由引理4知S能够满足(L1)→(R3).

设e=(i,1Tα,λ)∈B,i∈Iα,λ∈Λα,下面分两种情况证明.

1) 若∀f∈B(S),efe=ef,则对∀γ≤α,∀μ∈Λγ,f=(j,1Tγ,μ)∈B,有

efe=ef⇒(i,1Tα,λ)(j,1Tγ,μ)(i,1Tα,λ)=(i,1Tα,λ)(j,1Tγ,μ)

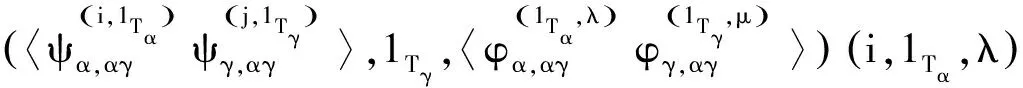
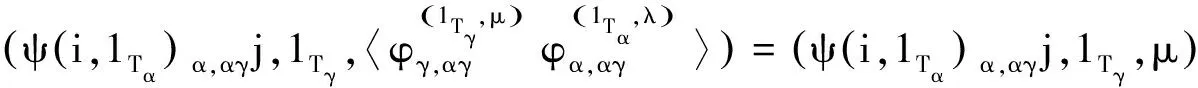
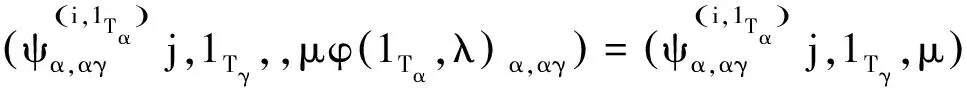
所以对∀μ∈Λγ,有μφ(1Tα,λ)α,γ=μ,即φ(1Tα,λ)α,γ=εΛγ.

2) 若∀f∈B(S),efe=fe,则对∀γ≤α,∀j∈Iγ,f=(j,1Tγ,μ)∈B,有

efe=fe⇒(i,1Tα,λ)(j,1Tγ,μ)(i,1Tα,λ)=(j,1Tγ,μ)(i,1Tα,λ)

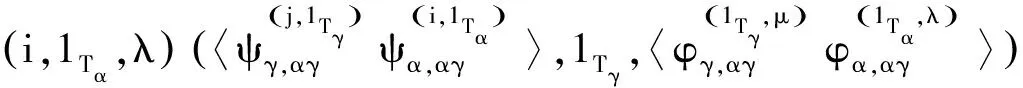
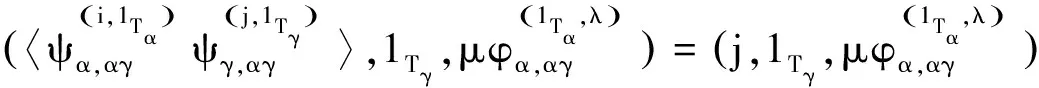
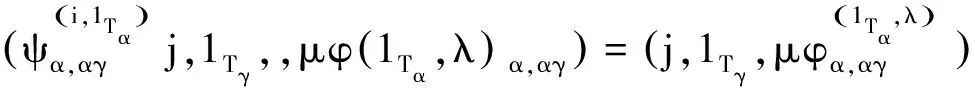
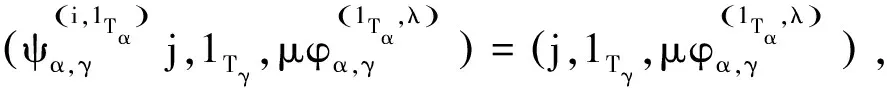
综上S满足条件(P),所以S能够这样构造.