L1-正则的最小二乘回归的加速随机梯度逼近算法

程一元 费经泰

（1.巢湖学院 数学与统计学院，安徽 巢湖 238000；2.安徽建筑大学城市建设学院 基础部，安徽 合肥 238076）

0 引言

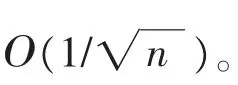
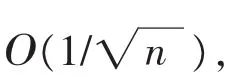
1 算法的提出

在本研究中考虑L1正则化的最小二乘回归加速梯度算法。其创新之处在于，可以得到非渐近速率为Ο（1n n/n）的收敛结果。为了给出随机加速梯度的收敛性质，对于回归问题的算法，提出以下假设：

假设（A—D）是随机逼近里的基本假设，与文献[8]假设相似。但与文献[8]比较本研究没有方差算子 H=E（xk⊗xk）的假设条件：E（ξi⊗ξi）≺σ2H。||θ||1是不可微函数，借助stoklev函数去逼近它。对于 δ>0，有

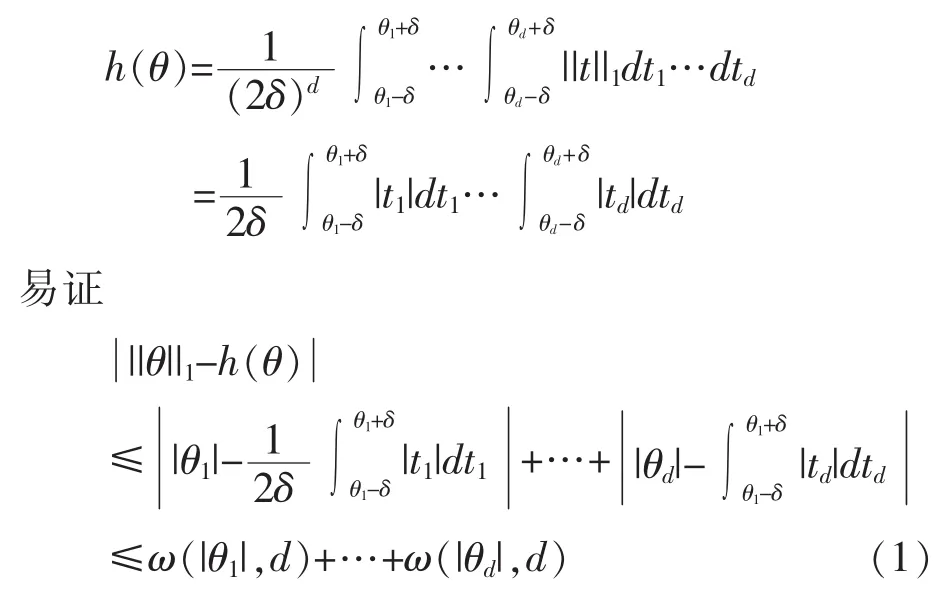
这里的 ω（||θ||，d）代表函数||θ||1的光滑模型。函数光滑模型的性质有

根据上面的分析，给出最小二乘的加速随机梯度算法：

算法1 最小二乘的加速随机梯度算法已知：θ0=α0=1，第 1 步：θag 0=θ0第 2步：θmd k=（1-αk）θag k-1+αkθk-1，第 3 步：zk=（▽g（θmd k ）+，▽h（θmd k ））/α2 k第 4 步：θk=θk-1-λkzk，第 5 步：θag k=θmd k-βkzk，第6步：k=k+1，返回到第二步直到满足精度要求。

2 算法的收敛性分析

为了研究加速随机梯度算法的收敛速度，借助文献[9]引理2.1，得到定理1。在定理1的基础上，分析研究最小二乘回归加速梯度算法的收敛性。

3 数值实验

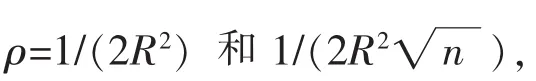
通过在两个不同噪声水平的合成噪声数据集上进行比较。图1是没有噪音下的，图2在噪音σ=0.1的水平下。从图中的比较可以看出，算法1的收敛速度要快于文献[4]和[8]的收敛速度。

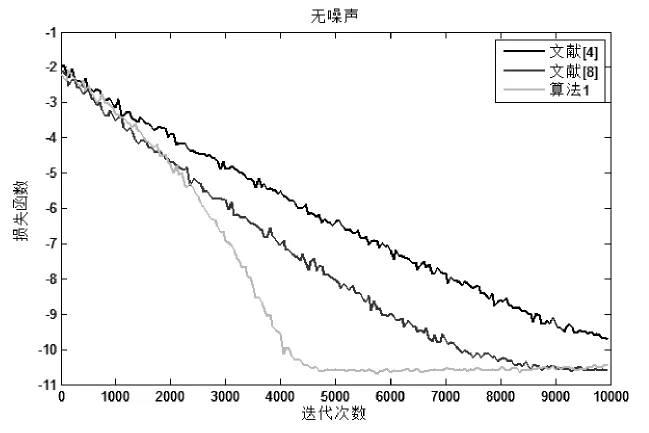
图1 无噪音下收敛速度的比较

4 结语

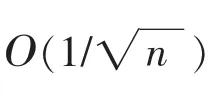
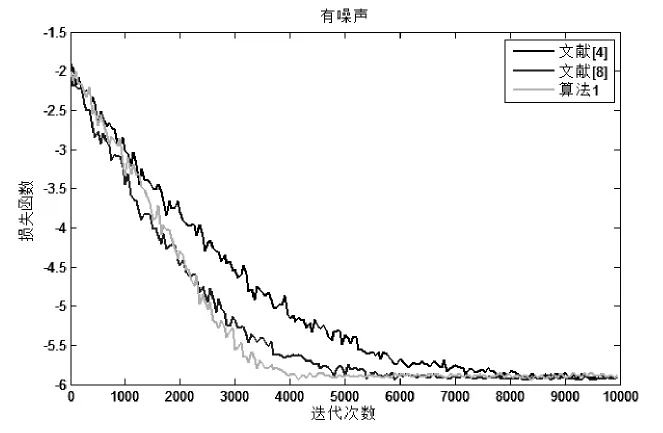
图2 有噪音σ=0.1下收敛速度的比较