基于博弈论的公交进站换道决策行为研究

巴兴强,刘娇娇

(东北林业大学 交通学院， 哈尔滨 150040)

公交车辆及其停靠站作为主要交通运输设施之一在城市道路上普遍存在，其驾驶员为顺利进站停靠而于站前一定范围进行的换道行为也屡见不鲜。这种换道行为既影响交通流的稳定运行，同时也危及该路段车辆的安全[1]。公交车辆在停靠站前必须完成换道准备进站停靠，因此在近站点范围内，驾驶员易采取激进换道策略，会造成目标车道后车减速、换道甚至排队，形成交通拥塞。更重要的是公交车由于其自身车型较大，在换道时会遮挡周围小汽车驾驶员视线，使其视野受阻，容易引发交通事故。因此，对公交进站换道行为的研究十分必要。

针对公交进站停靠的行为， LEE等[2]分析了公交进站停靠过程中影响社会车辆行驶的因素的权重，建立了因避让公交而需换道的社会车辆换道概率模型。JIN等[3]的研究论证了公交进站前的换道行为不仅会降低路段通行能力，对路段其他社会车辆的安全行驶也存在明显影响。吴立昱、尹小梅等[4-5]提出了考虑驾驶员特性的公交换道模型，分析了穿越车道数、换道始点位置、驾驶员性格特点等不同换道因素对路段交通流的影响规律。向艳红等[6]选取了交通量、离站路程、公交车数作为输入变量，建立了以进换点数为输出变量的BP神经网络模型，分析了各输入变量对公交进换行为的影响。汪济洲等[7]分析了公交进出站运动参数，应用聚类分析法训练了安全评价模型，对公交进出站三大阶段的安全性做了不同等级的评价。这些研究的重点主要集中在公交进站换道对路段其他交通要素的影响上，对公交车辆本身换道决策的研究尚少。本文通过建立公交强制换道概率模型与考虑公交驾驶员和目标车道跟随车驾驶员之间交互博弈的混合战略博弈模型，来分析公交进站换道的最优策略。

1 公交进站换道调查分析

1.1 强制换道特性

在无公交专用道的情况下，未行驶在停靠泊位所在车道的公交车辆进入直线式停靠站或欲进入港湾式停靠站时，均需在站点上游一定范围提前换道至停靠泊位所在车道准备进站并停靠，这种具有明显目的性和时间性的换道行为称之为公交强制换道。一般需要经历换道决策、实施换道、结束换道3个阶段，这里的换道决策行为并非指决定是否变道而是指决定变道的位置和方式[8]，主要受空挡的大小、相对速度和必须完成变道点的距离等因素的影响，尤其是与必须完成变道点的距离直接决定了驾驶员采取何种换道策略的概率。如图1所示，路段上社会车辆随机到达，行驶在车道2的公交车辆B1为避免交通冲突[9]，需等待车道1的社会车流出现可插车间隙，进行换道准备进站。由于可插车间隙出现的不确定性，公交换道位置随间隙分布在站点上游不同位置。

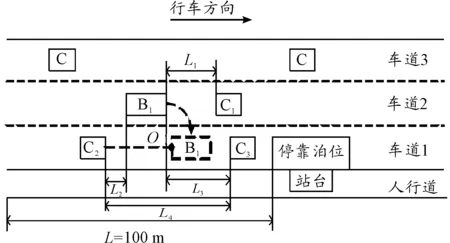
图1 公交车辆进站换道示意图

1.2 数据调查分析

为方便数据采集研究，本文对公交进站强制换道行为界定如下：在公交站点上游100 m范围内，由于停靠需求而在停靠站前从相邻车道驶入停靠泊位所在车道两车间隙的行为。选取哈尔滨和兴路双向6车道直线式公交站，以站点上游100 m为观测范围，在公交站点停靠泊位边线开始每隔10 m做出标记，利用摄影机记录早高峰(7∶00—9∶00)时间段内的公交进站换道行为。提取所需数据，对其进行初步分析筛选后，最终采集到116组数据用于数据分析，如表1所示。

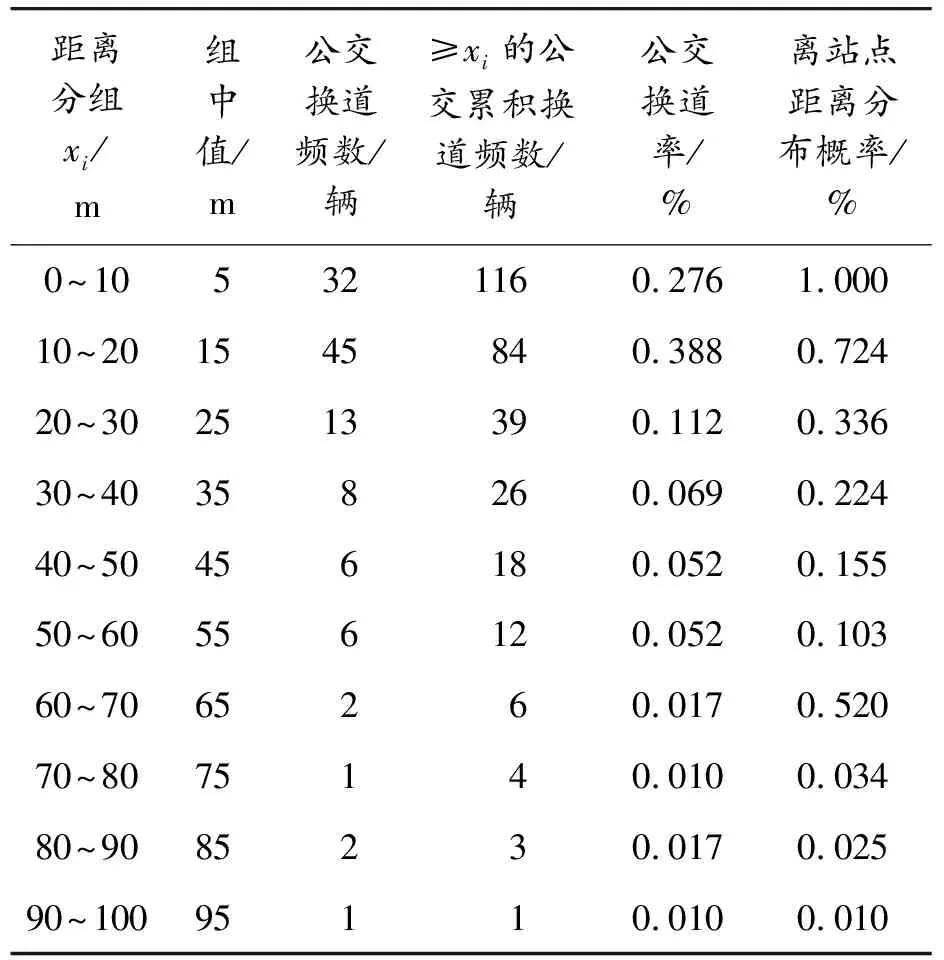
表1 公交车辆进站换道观测数据

从调查的数据中发现：公交进站强制换道不同于常规车道变换情况，而是有其独有特性。公交进站换道行为发生的位置主要集中在距停靠站距离较近(0～25 m)的区域；距站点25 m稍后，换道公交车辆急剧减少，少数车辆会在距站点较远位置进行换道；在无限接近停靠泊位处，换道分布概率接近于1。相应的换道率变化如图2所示，车辆换道位置距站点距离分布概率如图3所示。

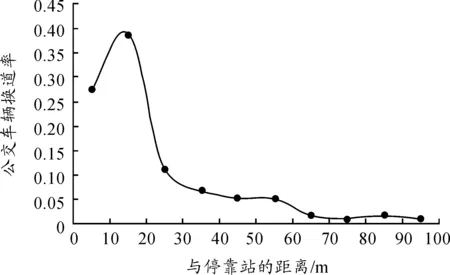
图2 公交车辆换道率

图3 距停靠站距离分布概率

2 公交强制换道建模

2.1 概率模型

强制换道与自由换道的区别通过换道概率表现出来[10]。如图2所示，在所调查路段，公交车辆换道率随与停靠站的距离的减小在某一位置急剧增加，换道位置和与停靠站的距离的分布概率曲线呈负指数趋势。这主要是由于换道必须在停靠站点前完成，越接近停靠站，公交车辆驾驶员换道意愿越迫切[11]，对可插车间隙的要求相应越小，此时驾驶员对行车的安全效益期望相对降低而更注重行车的时间效益。根据换道位置和与停靠站距离的分布概率曲线，本文引入基于公交位置的换道概率来描述驾驶员换道意愿，反映其对换道行为的渴望程度和公交位置与停靠站距离之间的关系。公交车辆驾驶员换道概率Pd的数学表达式为：

(1)

式中：Pd表示驾驶员换道概率,Pd∈[0,1]；α、λ为常数；L为停靠站前路段长度；x为公交车辆当前位置与停靠站之间的距离。

2.2 博弈模型

2.2.1 驾驶人换道判断决策分析

如图1所示，B1为当前车道研究对象即欲进站停靠的公交车，C1为当前车道前导车；C2、C3分别为目标车道(公交停靠泊位所在车道)跟随车及前导车；L1、L2、L3分别为当前正常行驶的公交车B1与社会车辆C1、C2、C3的实际距离；L4为C2与C3之间的跟驰距离。在停靠站上游一定距离处，公交车辆B1为顺利进站停靠，需要在停靠站点前从当前车道2寻找可插车间隙换道至目标车道1。

在换道决策阶段，换道公交车辆车B1首先寻找车道1车流中的可插车间隙，当其大于临界间隙时，B1向目标车道跟随车C2表明换道意图，跟随车C2驾驶员根据自身利益判断决定是否协作换道。若C2决定协作换道，就会主动减速扩大换道间隙，而换道公交车B1在判断该间隙能够满足自己安全换道要求时开始执行换道操作。若C2驾驶员在判断自身利益后，决定匀速或加速行驶而拒绝协作换道，此时，若距离公交停靠站过近，不足以等候下一可插车间隙出现，换道公交车B1就会强制插入间隙，跟随车C2被迫减速。若距站点的距离足够寻找下一间隙，公交车出于行车安全的考虑，就会减速行驶等待下一个适当间隙出现，驾驶人如此交互博弈进行决策判断，直到完成换道。

根据上述分析，对象车在实际换道决策过程中会重点关注目标车道跟随车的行驶状况，而周围其他车对其换道决策影响相对较小，本文将忽略不计，仅研究对象车与目标车道跟随车驾驶员之间的交互博弈。

2.2.2 换道博弈描述

博弈论主要研究决策主体在给定信息结构下如何决策以最大化自己的效用，以及不同决策主体之间的均衡[12]，任何博弈都须有参与人、策略、收益3个基本要素，且假设所有参与人均是理性的，即以自己最大化利益为目标。纳什均衡是博弈论中的重要概念，描述的是参与博弈单独个体针对其他参与者所选策略的最优反应策略的组合[13]。

如图1所示，O为临界冲突点，即若两车均按当前状态行驶一定时间后在该处可能发生交通冲突的临界点[14]。对于目标车道跟随车C2而言，若公交车辆B1换道成功，C2的前导车由C3变为公交车B1，显然这将使得C2的跟随车距受到挤压，降低C2驾驶员对行驶车速和空间的满意度，这样C2与B1的行驶需求就发生了冲突。假设临界冲突点为O，由于双方驾驶员作为理性人而存在，所以两者会采取不同的策略以最大化自身利益。C2驾驶员可采取减速让行或加速通过两种策略，让行于换道公交车B1使其率先通过冲突点O，避免碰撞，以保证自身安全效益；或者加速行驶，阻止B1换道，以保障自身行驶速度与空间。公交车B1可采取的两种策略则为等待换道或强制换道，以满足自身安全行驶或成功换道的需求。最终，两车争相率先通过临界冲突点O，形成具备竞争关系的二人博弈，称之为公交进站换道博弈。

在换道博弈过程中，驾驶人会根据不同情况以某种概率分布随机地选择不同的行动，而不是明确唯一的策略，因此彼此无法提前预知对方的决策，即无法通过合作策略来达到整体最优，属于非合作混合战略博弈，该博弈的均衡解便为纳什均衡解[8]。

2.2.3 收益与均衡

以自身收益最大化为目标的换道博弈过程中，换道公交车辆B1的收益由安全收益S、时间收益T和换道收益D三部分构成，其权重分别取α1、β1和γ，且α1+β1+γ=1；目标车道跟随车C2的收益则由安全收益S和时间收益T两部分构成，其权重分别取α2和β2，同样α2+β2=1。各权重系数的取值由驾驶员性格、心理特征、安全意识等因素共同决定，可通过问卷调查获得。据此，建立双方收益矩阵，如表2所示。

表2 博弈双方收益矩阵

混合战略博弈中，驾驶人以一定概率随机地选择不同的策略。设换道公交车辆B1驾驶员采用混合策略σb= (P,1-P),即驾驶员以P的概率选择强制换道，1-P的概率选择等待换道。目标车道跟随车C2驾驶员采用混合策略σc=(Q,1-Q),即驾驶员以Q的概率选择减速让行，以1-Q的概率选择加速通过。应用收益相等法求解混合策略纳什均衡。

根据收益矩阵与混合策略概率分布，计算公交车辆B1驾驶员在变道过程中的期望收益为

U1(P,Q)=PQ(β1T+γD)-P(1-Q)α1S-

(1-P)Q(β1T+γD)+(1-P)(1-Q)·

(α1S-β1T-γD)

(2)

车辆C2驾驶员的期望收益为

U2(P,Q)=PQ(α2S-β2T)+

(1-Q)P(β2T-α2S)-

(1-P)Qβ2T+(1-P)(1-Q)β2T

(3)

给定目标车道跟随车减速让行概率Q，则换道公交车辆B1的纯策略强行换道(P=1)或等待换道(P=0)的期望收益分别为

U11(1,Q)=Q(β1T+γD)-(1-Q)α1S

(4)

U12(0,Q)=-Q(β1T+γD)+

(1-Q)(α1S-β1T-γD)

(5)

令U11(1,Q)=U12(0,Q)，可解得：

(6)

当C2驾驶员采取减速避让的概率Q>Q*时，公交车B1驾驶员采取强制换道策略的收益更大；当Q

给定公交车辆换道概率P，则目标车道跟随车C2的纯策略减速让行(Q=1)和加速通过(Q=0)的期望收益分别为：

U21(P,1)=P(α2S-β2T)-(1-P)β2T

(7)

U22(P,0)=P(β2T-α2S)+(1-P)β2T

(8)

令U21(P,1)=U22(P,0)，可解得：

(9)

当公交B1驾驶员采取强行变道策略的概率P>P*时，C2驾驶员采取避让策略收益更大；当P

因此，可得该非合作混合战略博弈模型的纳什均衡为：

通过上述计算可知：若安全收益S的权重增大，时间收益T、换道收益D的权重会减小，这种情况下，Q*的值增大，表明C2驾驶员采取减速让行策略的纳什均衡点增大，B1驾驶员强行换道的可能会减小；相反，若减少S的权重，P*的值增大，表明B1驾驶员采取强行换道策略的纳什均衡点增大，C2驾驶员减速让行的可能会减小。这与驾驶员实际驾驶情况相符，即若增大交通事故的惩罚力度，或驾驶员安全意识比较强烈，则驾驶人会采取更为谨慎的行驶策略。

2.3 公交最优换道策略

综上分析，公交车辆驾驶员为顺利进站停靠而采取换道行为的决策主要与两大因素紧密相关，即车辆当前位置距停靠站的距离和目标车道跟随车的行驶状态。在进行策略选择时，考虑其行车时间延误、安全风险与换道迫切程度，以一定概率选择使自己期望效益最优的策略。根据公交换道概率模型，结合对换道过程中公交驾驶员与目标车道跟随车驾驶员之间博弈的纳什均衡的分析，可得：

U21(P,1)=Pα2S-β2T=

(10)

U22(P,0)=β2T-Pα2S=

(11)

纳什均衡点为

(12)

3 算例分析

根据调研与计算，标定式(1)参数L=100、α=0.02、λ=0.035。通过问卷调查与数据处理分析，设定行车的安全收益S=10、时间收益T=8，行车安全与时间重要度因子分别为α2=0.6、β2=0.4。将各数值代入纳什均衡点计算式(12)可得：

(13)

x=20

可知公交驾驶员在距停靠站20 m处以53.3%的概率选择强制换道策略准备进站为其最佳策略。该策略下，目标车道跟随车C2驾驶员采取减速让行和加速通过两种策略无差异的，其收益相同，但出于安全考虑，驾驶员采取减速让行的概率更大一些。根据图3，有超过60%的公交车辆在距离站点0～25 m的区间范围内进行换道，即驾驶员在权衡自身行车效益后，大多数会选择在此区间内进行换道准备进站停靠。计算结果与实际情况相符，说明本文建模过程符合实际情况中公交进站强制换道决策阶段的运行特征。

4 结束语

在对公交车辆换道进站行为调研的基础上，分析了公交换道率及换道位置距停靠站距离的分布概率，据此构造了公交强制换道概率模型。综合考虑公交和社会车辆驾驶员之间的交互博弈与上述强制换道概率模型，求得混合战略博弈的纳什均衡点，得到公交进站换道的理论最优策略。实际算例表明：公交进站换道决策的最优策略为在距停靠站20 m处，以53.3%的概率选择强制换道策略准备进站停靠。该结果与实际公交进站换道情况相符。因此，本文所建立的换道决策预测模型能够为欲换道进站公交车辆及其影响范围内的社会车辆的安全行驶提供理论参考。

公交驾驶员的行车安全效益、时间效益是在调研分析的基础上做出一定的假设，通过问卷调查分析的方式获取。驾驶人对于行车的效益往往难以统一定量。因此，在实际计算中，还需根据不同驾驶员对期望效益的衡量做出相应调整。