FSAE赛车转向系统优化设计

宋学前，丁华锋，景文倩，黄 成，朱令磊

(湖北文理学院 纯电动汽车动力系统设计与测试湖北省重点实验室， 湖北 襄阳 441053)

中国大学生方程式汽车大赛(简称“中国FSAE”)是一项由高等院校汽车工程或汽车相关专业在校学生组队参加的汽车设计与制造比赛。该项比赛旨在培养学生汽车设计成本控制、团队合作等能力。

转向系统是FSAE赛车重要的组成部分，转向系统设计的好坏直接决定了赛车的操纵稳定性。目前国内外对汽车内外转向轮转角的研究主要是满足阿克曼转向理论，没有考虑到实际转向过程中轮胎侧偏力对转向轮转角的影响。此外，FSAE赛车没有转向助力机构，传统的汽车转向力的分析研究也已经不再适用于赛车。例如，李君等[1]对转向轮转角的研究没有分析转向力的大小，可能导致实际转向过程中转向过重或过轻。熊坚等[2]通过对前轮主销空间定位以及车轮绕主销的空间旋转变换推导转向力，该方法只能得到右前轮总的转向力矩，无法计算出方向盘力矩与右前轮力矩的关系，难以对转向的设计进行指导。王润琪等[3]虽然对汽车前轮回正力矩和转向力矩进行了分析计算，但主要分析了主销定位参数，没有分析转向结构参数对转向力的影响，不利于优化转向结构来控制转向力，而且对汽车转向力的分析不适用于赛车。罗欣等[4]提出通过对转向轮转角加权来优化目标函数的方法，并未考虑到转向侧偏力对轮胎转角的影响，赛车高速过弯侧偏力较大时分析结果误差较大。向铁明等[5]对断开点的分析以理想阿克曼转角关系为目标，与实际有所偏差，且没有对断开点的初始坐标进行理论分析。石启龙等[6]利用Matlab中最小二乘法进行转向梯形的优化也将轮胎视为刚体，忽视了转向过程中轮胎变形对转向轮转角的影响。张祥勃等[7]在优化转向梯形结构时对转向力的研究不够全面，仅是定性的分析，没有实际的计算。以上对转向力的分析都没有涉及转向系统的结构参数，分析结果无法对转向的设计进行指导，而对转向轮转角关系的研究都主要以理论阿克曼转角关系为目标进行分析，忽视了侧偏力对轮胎转角的影响，而FSAE赛车转向速度快，轮胎所受到的侧偏力较大，分析的误差也会较大[8-11]。上述文献对转向结构参数的分析研究只是某一方面的研究，分析的结果不够全面[12-16]。

本文通过对转向系统的动力学分析模型进行分析，确定转向梯形结构参数的取值范围，赛车转向力大小适中，使得转向不会过重而增加车手负担，也不会过轻而缺乏路感，同时提高转向系统的灵敏度；再利用Adams软件对转向断开点空间坐标进行优化，减小轮跳对转向的冲击和对前束角的影响，从而确定了部分转向参数的取值；最后通过对理想阿克曼转向关系的分析矫正消除因侧偏力引起的分析误差，同时通过对阿克曼矫正率和阿克曼率大小的对比分析，使结果更加准确可靠。

1 转向系统转向力的分析计算

与汽车相比，FSAE赛车转弯半径更小，转向过程中速度更快，且无助力转向系统。赛车的转向力由赛车手的手力提供，赛车转向力的大小直接影响赛车的操纵性和转向的灵敏性，故对转向结构参数进行分析优化、调节转向力的大小尤为重要。FSAE赛车转向系统结构参数如表1所示，模型如图1所示。

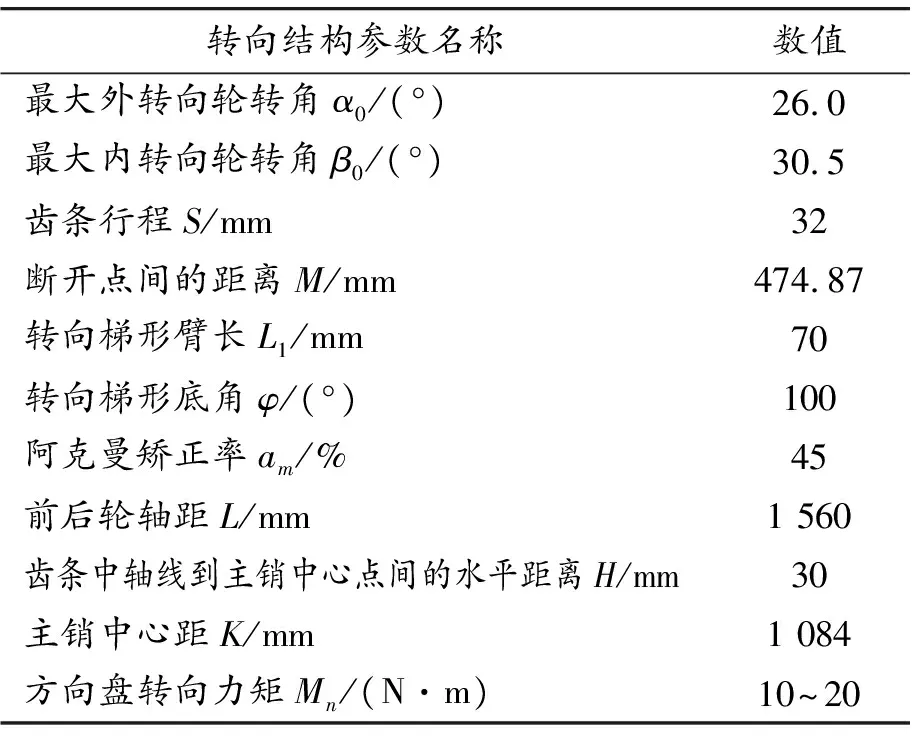
表1 转向系统结构参数

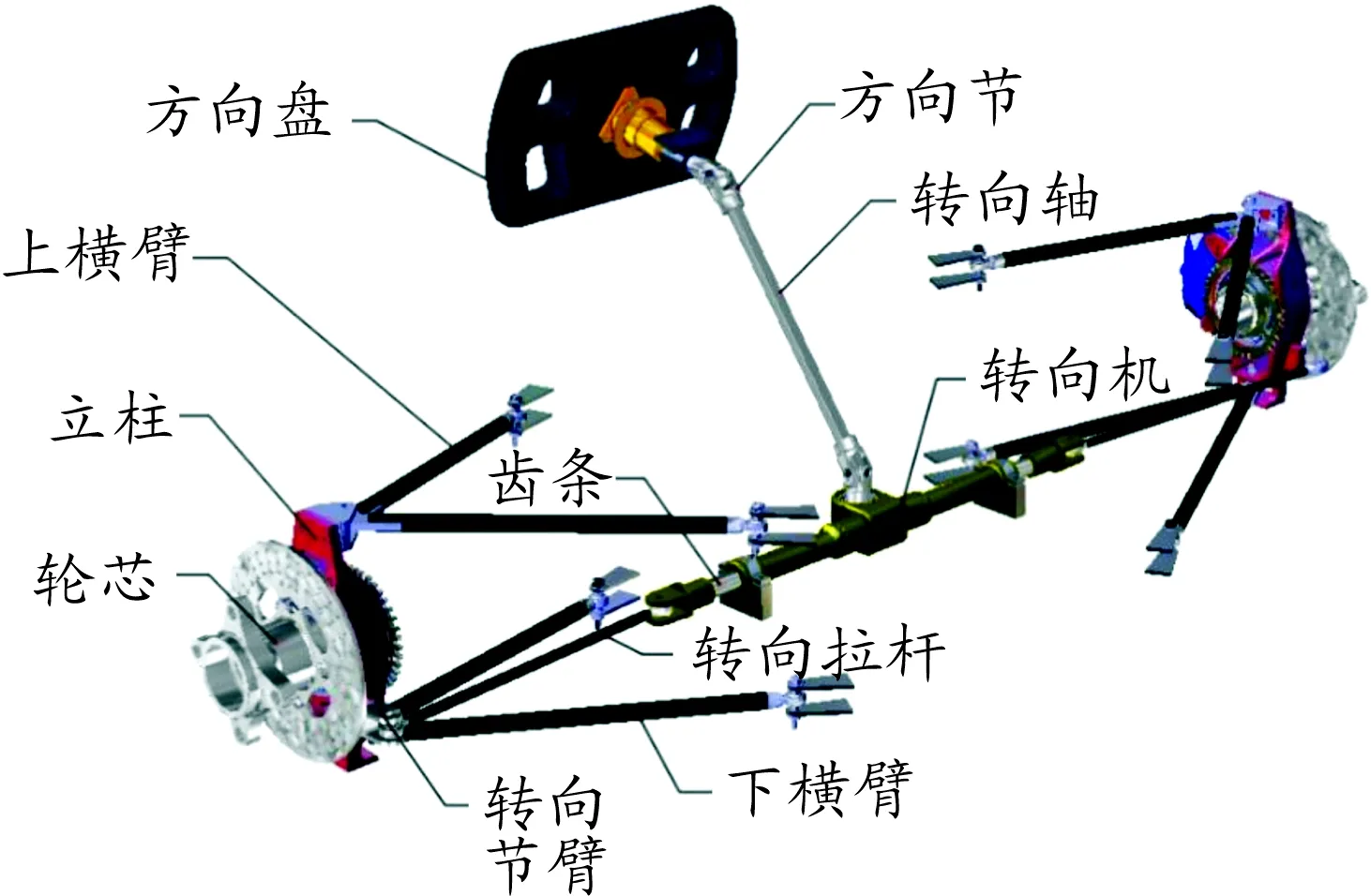
图1 转向系统模型

将以上断开式转向梯形结构的三维模型转化为物理模型并进行动力学受力分析，分析示意图如图2所示。

图2 转向梯形结构受力分析

FSAE赛车转向系统无转向助力机构，方向盘上的力距通过转向传动机构直接作用到转向齿条上，齿条轴向力F的大小与左右拉杆对齿条的拉力FL和推力FR的合力大小相等。拉杆L2通过杆端关节轴承分别与转向节臂L1和转向齿条相连接，左拉杆同时受到齿条的推力F1和左节臂的拉力F2，右拉杆同时受到的齿条推力F3和右节臂拉力F4，左拉杆受到的拉力F2和左节臂受到的推力Fβ为相互作用力。右拉杆受到的拉力F4和右节臂受到的拉力Fα也为相互作用力。齿条和转向节臂对拉杆L2的作用力大小相同而方向相反。转向梯形臂L1绕主销转动时，由于地面与轮胎间的摩擦力及其主销结构参数作用所产生的回正力的影响，转向节臂转动时会有一个阻力矩，左右转向轮所受到的转向阻力矩分别为Mp和Mq，左右转向轮转角大小分别为α和β。

对内转向轮主销中心点O1点起距：

Fβ·cos(θ1)·L1·sin(φ-β)-

Fβ·sin(θ1)·L1·cos(φ-β)=Mp

(1)

Fβ=F1=F2=FL·cos(θ1)

(2)

其中内转向轮的传动角为

(3)

对外转向轮主销中心点O2点起距：

Fα·cos(θ2)·L1·sin(φ+α)-

Fα·sin(θ2)·L1·cos(φ+α)=Mq

(4)

Fβ=F4=F3=FR·cos(θ2)

(5)

其中外转向轮的传动角为

(6)

转向横拉杆的长度为

(7)

方向盘上的力矩Mn与齿条轴向力(FL+FR)的关系为

(8)

式中：Z为齿轮齿数；m为齿轮模数；H为齿条轴线到主销中心点连线间的距离。

轮胎所受的侧偏力主要由主销后倾角的作用产生的回正力矩、主销内倾角的作用产生的回正力矩及其轮胎与地面的摩擦力作用产生的阻力矩3部分构成。

赛车转向桥主销上端向后倾斜一个γ角，称为主销后倾角，其主要作用是使转向轮形成自动回正力矩，保持汽车行驶的稳定性。当主销具有后倾角γ时，其轴线与路面的交点将位于转向轮与路面接触点的前面，当赛车转向时，离心力方向与轮胎转动方向相反，在转向轮与地面接触点处，离心力使转向轮绕主销轴线形成回转力矩M1，此力矩在转向时为阻力矩而在方向回正时为主动力矩，主销后倾角的作用产生的回正力矩大小为

(9)

式中：e为轮胎轴线到地面的距离；γ为主销后倾角的大小；m0为赛车左前轮、右前轮配重；v为赛车的行驶速度；R为外转向轮转弯半径；r为内转向轮转弯半径。

在主销内倾的条件下，由重力作用导致的车轮回正力矩公式为：

2·fv·m0·g·e

(10)

当回正力矩使转向轮回正时，赛车被抬高所产生的重力势能除了转化为轮胎回正所做的功外，还转化为轮胎与地面间的摩擦内能。轮胎与地面间的当量摩擦因数为fv，则因内能而损失的力矩为Mf=fv·m0·g·e。

转向时轮胎与地面之间存在摩擦力，摩擦力的作用点为轮胎与地面的接触点，力的方向为赛车行驶的方向。摩擦力与主销中心点间的垂直距离为c，转向轮与地面间的摩擦力矩的计算公式为：

M3=m0·g·c·fv·(cos(α)+cos(β))

(11)

转向时总的转向力矩为3部分转向力之和：

MZ=Mp+Mq=M1+M2+M3

(12)

方向回正时总的转向力矩为

MZ=Mp+Mq=M3-M1-M2

(13)

联立式(1)～(13)即可求出方向盘上的转向力矩Mn与内外转向轮阻力矩的关系。

通过对赛车转向力进行分析来优化转向梯形结构参数，FSAE赛车转向力的分析结果表明：梯形臂长对转向力影响最大，当梯形臂长增大而其他条件不变时转向力减小，转向变轻，同时转向角传动比变小，转向响应变慢，转向灵敏性降低。梯形底角对转向力影响较大，断开点间的距离等参数对转向力影响相对较小，且转向力增大时相应的转向角传动比也会适当增大，转向变得沉重，而转向响应加快，灵敏度提高。FSAE赛车转向系统不宜过重增加车手负担，同时要求要有大的转向传动比，提高转向的过弯性能。赛车调试的结果显示，方向盘输入的转向力为10～20 N·m时，转向力大小适中，转向灵敏性和稳定性良好。通过Matlab对转向力分析得到梯形臂长的取值范围为65～85 mm，梯形底角的取值范围为70°～120°，而转向断开点间的距离M及齿条中轴线与主销中心线连线间的距离H对转向系统转向力的影响并不大，需要对转向断开点的空间坐标进行进一步的优化。

2 转向断开点空间坐标的分析优化

方程式赛车转向系统采用断开式结构，赛车行驶过程中因路面不平造成赛车轮胎上、下跳动时转向节臂球头销中点U和横拉杆铰接T点的位置产生相对的变化，又因转向横拉杆的长度保持不变，轮胎跳动会对转向系统造成一定的冲击，同时必然也会引起轮胎前束角的变化，造成赛车跑偏，所以断开点的位置对转向系统的操纵性和稳定性影响较大。要减小轮胎上、下跳动对前束角的影响，必须使转向过程中转向横拉杆轴线始终指向立柱的瞬心。图3是上、下横臂不平行时的结构，已知双横臂的上横臂NP、下横臂MQ及转向节臂球销中心U在该平面的投影位置，绘制NP、MQ的延长线求得立柱MN的瞬心O1点，再由O1点作直线O1U；由MN、QP的延长线得O2点；绘UN的延长线，再过O1点作直线与UN的延长线交于O3点，并使O3O1线与O2O1线的夹角等于O1M与O1U线的夹角α，过O3点作O3P的延长线交O1U于T点，T即为断开点。当上、下横臂NP与MQ平行时结构如图4所示，则求出O2点后，过O2点绘平行于MQ平行线，再在UN的延长线上找出一点，使该点与过O2点的平行线的垂直距离等于U点至MQ线的垂直距离，这个点即为O3点，再绘O3P的延长线交于过U并平行于MQ的线于T点，T点即为断开点。通过Adams仿真分析，进一步优化断开点的坐标。

图3 上、下横臂不平行时的结构

图4 上、下横臂平行时的结构

利用Adams/car建立前悬架动力学模型，如图5所示。

图5 赛车悬架和转向机构样机模型

输入的悬架平行跳动为±30 mm，将以上断开点参数作为优化的初始值，赛车在未转向的状态下设置转向前束角为-1°。在每一次仿真里，Adams/Car可以自动计算出前束角的变化特性，再通过Adams/postprocessor图像处理模板得到最终图像，分析结果如图6所示。

图6 前束角随轮跳变化曲线

从图中可以看出，在车轮平行跳动中，前束角的变化范围为(-1.606°～-0.457°)，在轮胎上跳过程中前束角呈增加趋势，一般要求前束角在上跳过程中呈减小趋势，本文中前束角变化量为1.149°，不在理想状态，需要进行优化。再在Adams/car中对双横臂前悬和转向系统进行联合优化分析，通过优化转向节臂球销中心和横拉杆铰接点的空间坐标来减少轮胎前束角的变化。图7为参数优化后的对比图，实线为优化前的仿真曲线，虚线为优化后的仿真曲线，前束角变化范围为(-1.135°～-0.924°)，变化量为0.211°，变化明显减小，并且变化趋势合理。并输出轮胎前束角随轮胎上、下 跳动的关系图像。

通过对转向断开点的研究，确定了断开点间的距离为474.87 mm，齿条轴线与主销中心点连线间的水平距离为30 mm，同时确定了转向梯形的位置高度及其布置方式。

图7 优化前和优化后前束角变化

3 转向梯形结构参数分析与优化

转向梯形结构参数的取值影响赛车转向轮转角的大小，当赛车转向轮转角大小不合理时，转向轮会产生一定的侧滑，使赛车偏离理想转向路线的同时加剧轮胎的磨损，赛车的过弯性能变差。

赛车转向过程中要实现轮胎做纯滚动而不产生侧滑，四转向轮的速度瞬心必须交于同一点。也就是要符合理想阿克曼转角关系：

(14)

式中：α为理想外转向轮转角；β为理想内转向轮转角；K为两主销中心点间的距离；L为轮距。

实际转向过程中转向轮的转角与理论分析的转角之间总存在一定的偏差，偏差的大小用阿克曼率表示，阿克曼率αk定义为：

(15)

式中：α0为实际外转向轮转角；β0为实际内转向轮转角。

阿克曼率反映实际转向轮转角与理想转向轮转角的偏差，但由于侧偏力的存在，转向过程中轮胎受到侧偏力的作用会产生一定的形变，使实际转向轮转角小于理论设计的转向轮转角。以理想阿克曼转角关系为目标来优化内外转向轮转角会产生较大的分析误差，所以必须对理想阿克曼转角关系进行矫正分析，以消除因侧偏力引起的误差。定义阿克曼矫正率am：

(16)

式中α1和β1为对理想内外转向轮转角进行矫正后的内外转向轮转角，称为矫正后的转向轮转角，矫正后的转向轮转角消除了因侧偏力引起的分析误差，以矫正后的转向轮转角关系作为设计的目标来优化转向梯形参数能使设计结果更加准确，其中阿克曼矫正率反映侧偏力对转向轮转角影响的程度。由以上分析可以得到矫正后的外转向转角为

β1=am(β-α1)+α

(17)

赛车常用断开式转向梯形结构与独立悬架相配合，以保证一侧车轮上、下跳动时不会对另一侧车轮造成影响。转向时，转向机齿轮带动齿条移动，在横拉杆推力和拉力作用下，内转向轮和外转向轮转动会各自产生一个转角，如图2所示。由以上数学模型可以得到设计的理论内外转向轮转角。

内转向轮转角：

(18)

外转向轮转角：

(19)

齿条的单侧行程为：

(20)

式中：L1为梯形臂长；φ为梯形底角的补角；S为齿条单侧行程；α0为理论外转向轮转角；β0为理论内转向轮转角。

由以上分析可知，内外转向轮转角大小主要由梯形臂长L1、梯形底角φ、齿条中轴线到主销中心点连线的水平距离H、转向断开点间的距离M决定，而前面在对转向力的分析和对转向断开点位置的分析中，已经确定了齿条中轴线到主销中心点连线的水平距离H和转向断开点间的距离M，以及限定了梯形臂长L1和梯形底角的补角φ的取值范围，还需要通过对转向轮转角的分析确定最终梯形臂长和梯形底角的大小。

如图8、9所示，利用Matlab软件，根据式(14)～(17)即可做出矫正后的内外转向轮转角关系曲线，即α1-β1曲线，根据式(18)、(19)可做出内外转向轮理论转角的关系曲线，即α0-β0曲线，并用理论转角的关系曲线去逼近矫正后的转角关系曲线。两曲线越接近，表明理论转角关系越接近矫正后的转角关系。由式(15)可求出阿克曼率随外转向轮转角间的关系曲线。阿克曼矫正率为侧偏力对转向轮转角影响的程度，不随内外转向轮的大小而变化，阿克曼率关系曲线与阿克曼矫正率关系曲线理论上相重合，但理论转向轮转角不可能与矫正后的转向轮转角完全相同，故两曲线之间存在误差。两曲线误差的大小反映优化的偏差，直接决定优化结果的好坏。

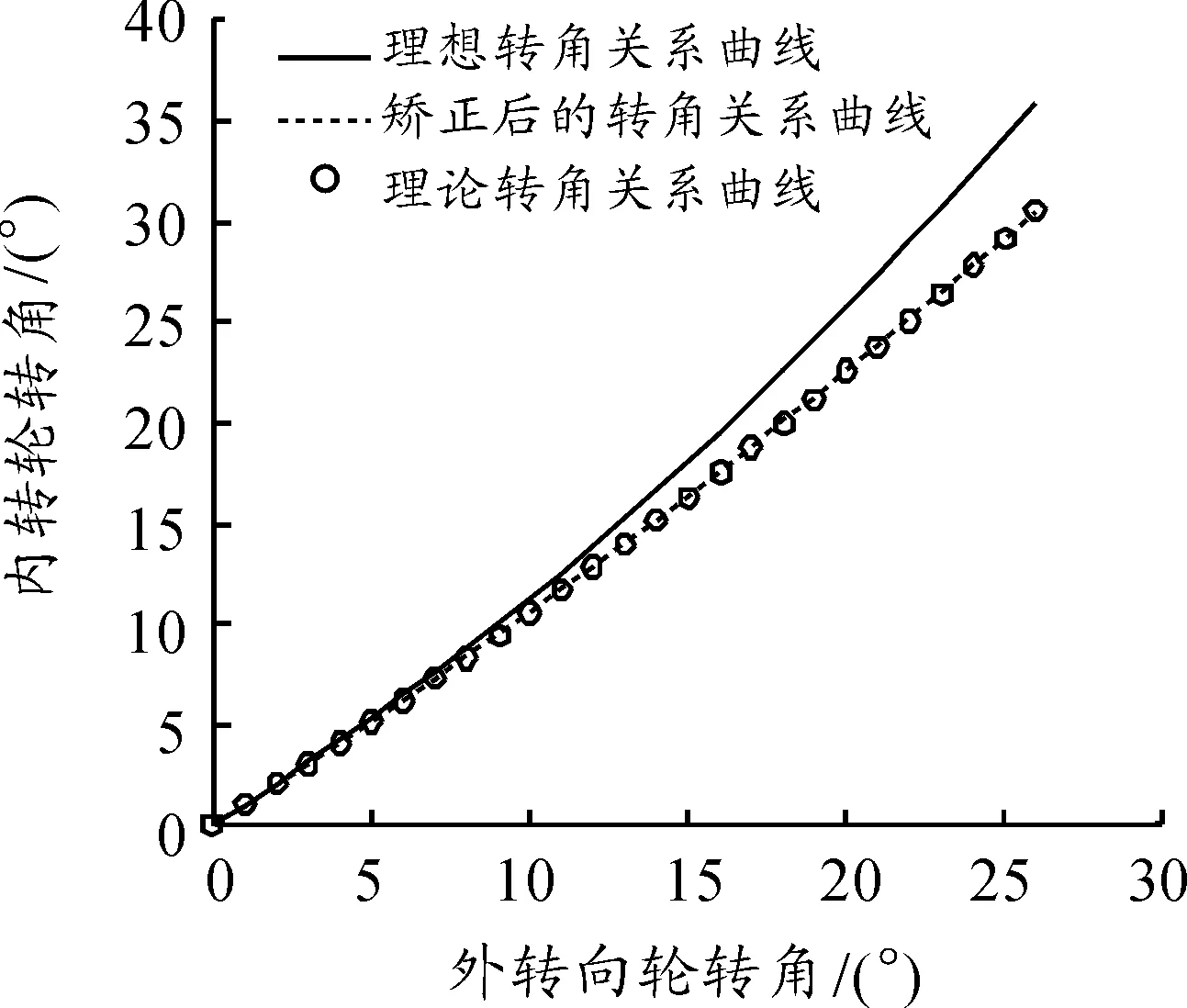
图8 内外转向轮转角关系曲线

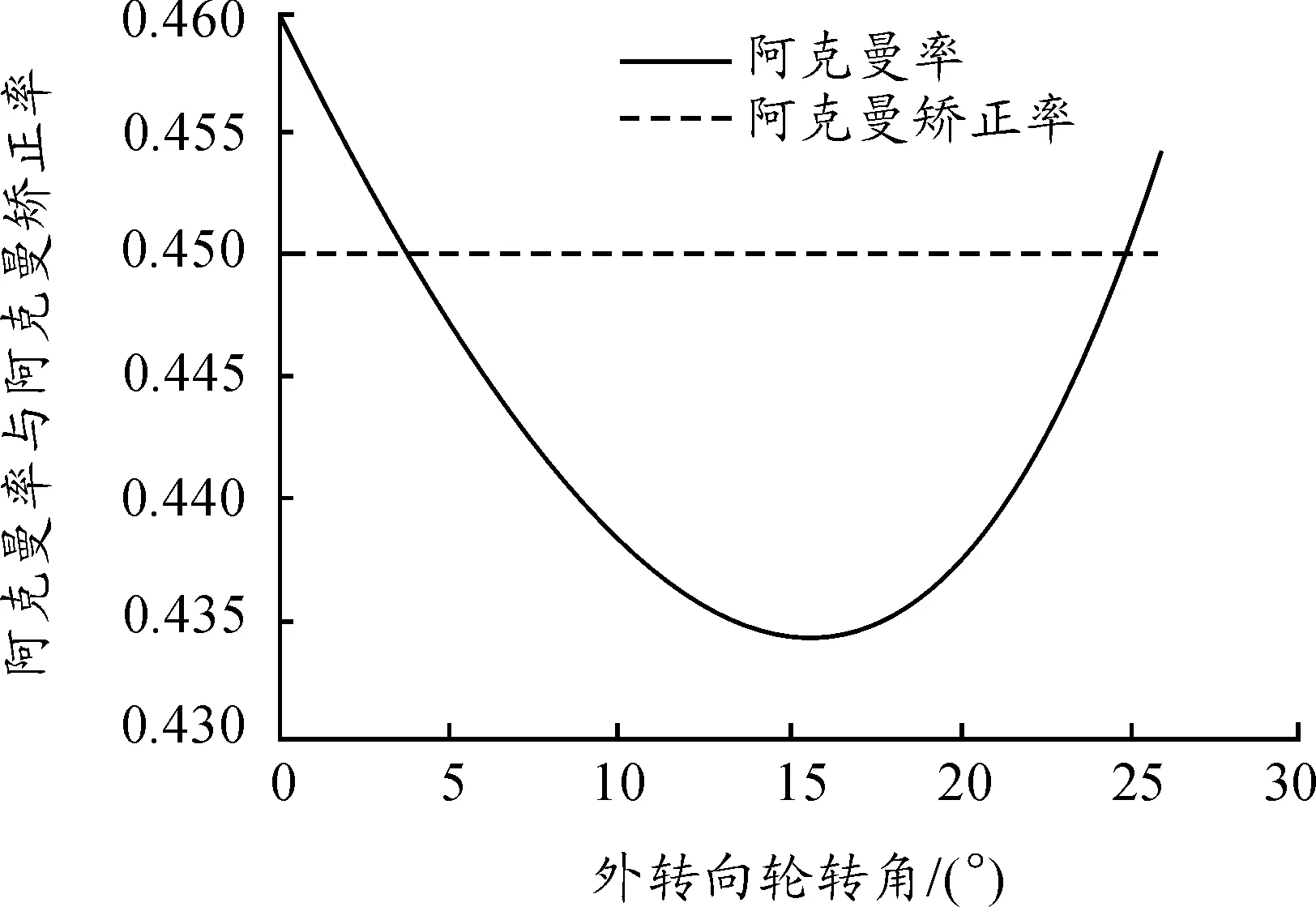
图9 外转向轮转角与阿克曼率关系曲线

在Matlab中修改梯形臂长度和梯形底角的大小，利用最小二乘法计算出阿克曼率与阿克曼矫正率的偏差，分析结果表明：当阿克曼矫正率取值为45%、梯形臂长为70 mm、梯形底角为110°时，利用实际转向轮内外轮转角的关系曲线去逼近矫正后的内外转向轮转角关系曲线，两曲线接近重合。而外轮转角从0°增加到26°时实际阿克曼率在43%～46%，与阿克曼矫正率相差不大，分析结果较理想。

4 结论

对FSAE赛车特定的转向结构进行了分析，通过对转向系统转向力、转向断开点空间坐标、转向轮转角的综合分析计算，利用Adams软件进行了转向参数优化,使转向系统的综合性能良好，得到如下结论：

1) 转向力主要由转向梯形臂的长度和梯形底角决定，当赛车转弯半径不变，梯形臂长度减少或梯形底角由90°增大或减少时，方向盘转角将会增大，转向传动比减小。赛车转向响应变慢，灵敏度降低，但转向力增大，转向变沉重。通过合理的转向力限定转向梯形臂的长度和梯形底角的角度，提高了FSAE赛车转向系统的操纵性。

2) 用Adams对转向断开点空间位置的分析使转向轮上、下跳动时前束角的改变量达到最小，通过对转向断开点空间坐标的分析确定断开点间的距离，也确定了转向齿条中轴线到主销中心点连线间的距离，提高了转向的稳定性。

3) 通过对理想内外转向轮转角的分析矫正，消除了侧偏力引起的分析误差，进一步减少了轮胎的磨损，提高了转向系统的过弯性能，阿克曼矫正率为45%，实际转向过程中阿克曼率在43%～46%，其中外转向轮转角为15°时分析误差达到最大，最大阿克曼误差小于2%，分析结果较小。通过对转向轮转角的分析，完成了对转向系统结构参数的优化。