疫苗作用具有阶段性和环境传播的传染病模型的全局渐近稳定性

靖晓洁，赵爱民，刘桂荣

(山西大学 数学科学学院, 太原 030006)

近年来，许多关于传染病动力学的研究工作考虑了接种疫苗，并取得了一些较好的研究成果，见文献[1-4]。在这些研究成果中，很少考虑注射疫苗的阶段性[5]。对于一些传染病，如麻疹病毒，注射疫苗分为两个阶段：第1次接种后，被接种者仍会被感染，但比未接种者感染概率会降低；第2次接种完成后，由于抗体可以持续很长时间，可以认为接种者不会被感染。此外，由于一些传染病病毒在空气中和在被染病者接触过的物品、食物等的表体上存活时间较长，进而促进传染病的暴发，因此环境[6]也是传染病传播的重要因素。为此，本文考虑疫苗作用的阶段性特征和环境传播的SVEIR传染病模型，通过构造李雅普诺夫函数，证明了模型平衡点的全局渐近稳定性。

1 传染病模型

将个体分为6类：易感者S、第1次接种疫苗者V1、第2次接种疫苗者V2、潜伏者E、染病者I和恢复者R。忽略因病死亡，并加入环境因素，用S(t)、V1(t)、V2(t)、E(t)、I(t)、R(t)和B(t)表示t时刻易感者、第1次接种疫苗者、第2次接种疫苗者、潜伏者、染病者、恢复者和环境中传染病病毒的数量，建立如下数学模型:

(1)

其中：A为总人口的常数输入；μ为自然死亡率；β为人与人的感染率；α为人与环境的感染率；ν为第1次疫苗接种率；δ为第2次疫苗接种率；ε为降低感染率的比例；p为潜伏者进入染病者的比例；γ为染病者的恢复率；k为染病者排放到环境中的病毒的速率；τ为环境中病毒的失效率。显然模型(1)的子系统：

(2)

封闭。故本文只分析模型(2)。

事实上，由模型(2)的前4个方程有

于是可得

进而

是模型(2)的正不变集。以下在Ω上研究模型(2)的动力学行为。

2 基本再生数和平衡点的存在性

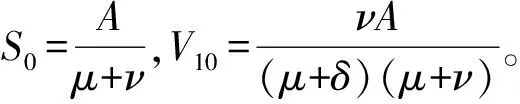
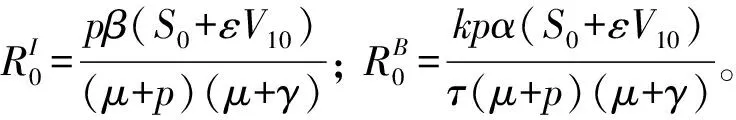
下面考虑模型(2)的地方病平衡点的存在性。

考虑下列代数方程组

(3)

由方程组(3)的第4、5个方程可得

(4)

3 平衡点的全局渐近稳定性

定理1 当R0<1时，模型(2)的无病平衡点P0(S0,V10,0,0,0)在Ω上是全局渐近稳定的。

证明根据模型(2)的无病平衡点P0(S0,V10,0,0,0)，模型(2)可改写为

(5)

定义Lyapunov函数L1∶Ω→[0,∞)为

函数L1沿着模型(5)的全导数为

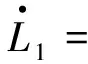
(βI+αB)[(S-S0)+ε(V1-V10)+(S0+εV10)]-(μ+p)E+

证明根据方程组(3)，模型(2)可改写为：

(6)

再定义Lyapunov函数L2∶Ω→[0,∞)为

函数L2沿着模型(6)的全导数为

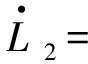
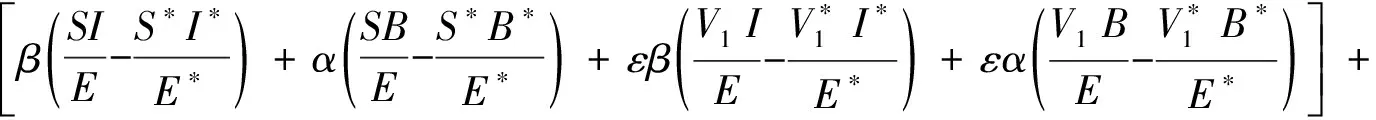
由方程组(3)可知

进而有，

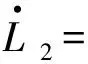
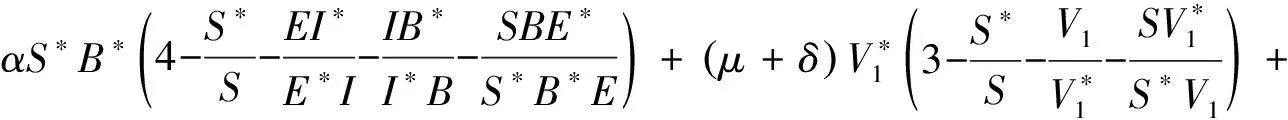
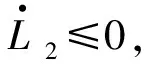
4 数值仿真

为了验证以上的理论分析，进行了数值模拟。选取参数β=0.000 25，α=0.000 05，μ=0.000 01，ε=0.018，ν=0.85，δ=0.75，p=0.6，k=2，τ=4，γ=0.9。

令A=100，进而R0≈0.052 1<1。因此，模型(1)的无病平衡点是全局渐近稳定的。图1验证了该结果的合理性。

令A=10 000，进而R0≈5.217 9>1。因此，模型(1)存在唯一的地方病平衡点，且是全局渐近稳定的。图2验证了此结论的正确性。

图1 R0<1时，E(t)+I(t)的时间序列图

另取参数A=10 000，β=0.000 25，α=0.000 05，μ=0.000 01，ε=0.018，p=0.6，k=2，τ=4，γ=0.9。图3中δ=0.5，取3组不同的ν的值。可明显地观察到：随着ν的增大，E(t)+I(t)有显著下降，最后趋于稳定(即地方病平衡点)。图4中ν=0.5，取3组不同的δ值可以看到：当δ增大时，E(t)+I(t)随之减少并趋于稳定(即地方病平衡点)。对比发现，第1次疫苗接种率ν的增加可明显地减少潜伏者和染病者的数量；第2次疫苗接种率δ的增加也能减少潜伏者和染病者的数量，但减少量没有第1次疫苗接种率ν明显。由此可见，潜伏者和染病者对第1次疫苗接种率更敏感。

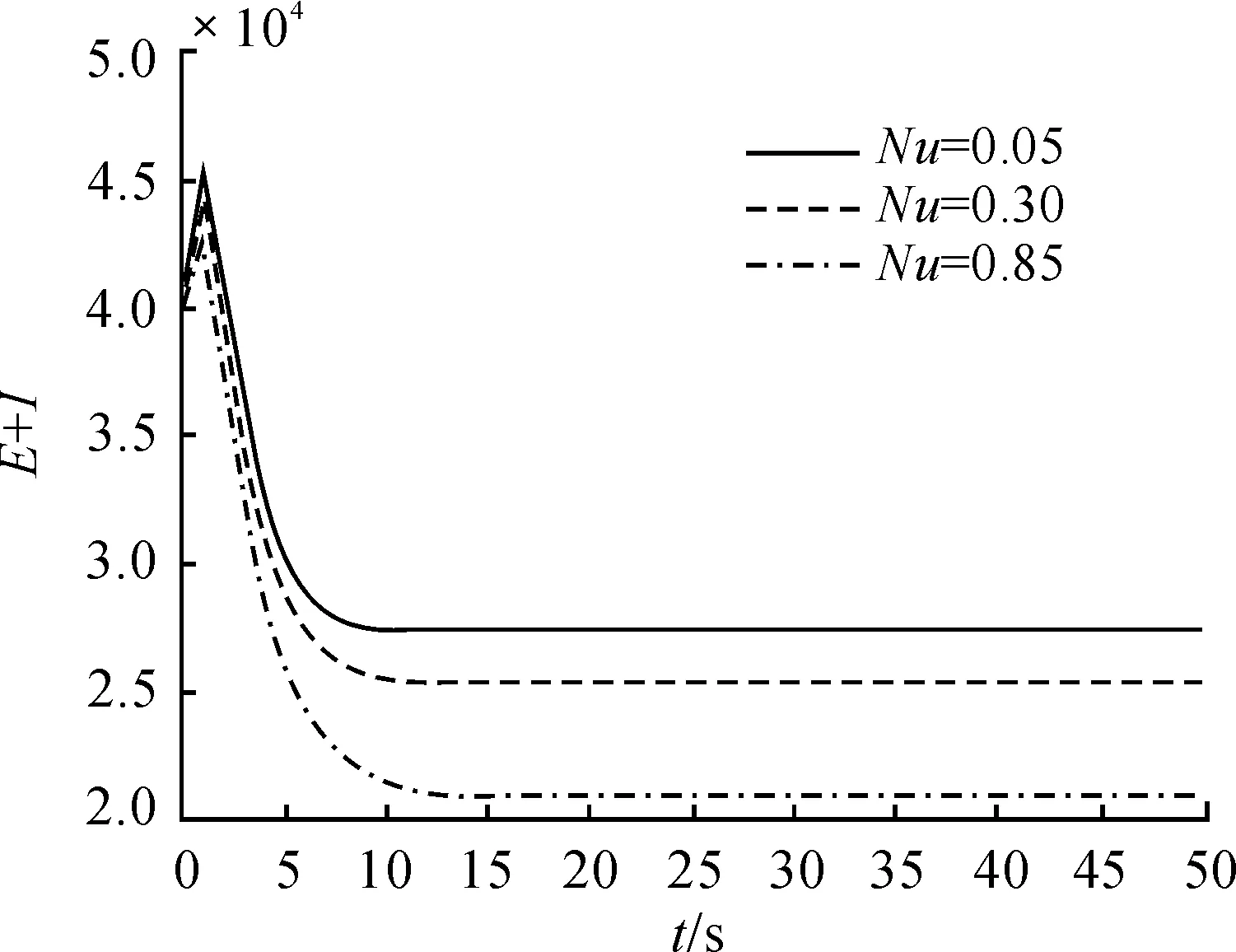
图3 ν变化时，E(t)+I(t)的时间序列图

5 结束语

本文把疫苗分为两个阶段V1和V2，结合带有环境传播和潜伏期特征的传染病，在文献[5]的基础上，更细致地研究了一类传染病的全局性态，得到了传染病的基本再生数R0。证明了：当R0<1时，无病平衡点是全局渐近稳定的；当R0>1时，地方病平衡点是全局渐近稳定的。通过数值模拟验证了本文研究结果的正确性，同时还模拟了第1次疫苗接种率ν和第2次疫苗接种率δ对潜伏者和染病者的影响。通过模拟发现：加大第1次疫苗接种率可大幅度减少潜伏者和染病者的数量。本文的研究有利于流行病学家们有的放矢地采取相应的干预措施，对防止传染病的暴发、流行具有重要的理论价值和实际意义。