飞机的风挡及舱盖气压分布计算与分析

吴 冬

(西安航空职业技术学院， 西安 710089)

飞机在飞行过程中，风挡座舱盖要受到气动压力的作用。飞机在高空高速飞行过程中，与其周围的空气发生相互作用，使得机表受到一定的表面力，而沿表面法线方向的正压力就是风挡及舱盖体系的外表面的气压。风挡及舱盖整体承受风压和温度荷载，存在失效破坏的可能性很大。Hajela 等[1]利用全局敏感度方程探索了飞机气动、性能、结构、控制一体化设计的方法。毛坤等[2]研究了传热、结构强度、屈曲和模态之间的影响，优化了风挡及舱盖系统。郑军超等[3]研究了温度场及温度梯度对风挡结构强度的影响。朱书华等[4]研究了鸟撞对风挡的影响。刘振侠等[5]研究了舱盖的热疲劳性能。张志林等[6]分析了飞机座舱有机玻璃结构疲劳寿命估算的局部应力法。彭迎风等[7]对飞机风挡鸟撞动响应进行了研究。杨燕初等[8]研究了基于遗传算法的临近空间飞艇多学科优化设计。虞跨海等[9]研究了多学科耦合作用下的涡轮叶片复杂结构快速设计优化技术。冯毅等[10]研究了飞行器参数化几何建模方法。高度等[11]对吸气式高超声速飞行器多学科优化设计进行了研究，罗利成等[12]研究了飞机座舱有机玻璃材料的疲劳性能。

已有研究对风挡及座舱的气动性能，特别是整体部件气压的分析比较少，因此本文通过建立风挡及舱盖的有限元模型，重点分析了脊线上各点的气压分布情况，为其他学科的优化设计提供一定的数据参考。

1 气动分析理论

气动分析采用黏性可压缩的模型，描述流动的基本方程为：

1) 动量守恒方程

采用笛卡儿坐标系描述空气流动，在3个坐标方向上，气流相对运动方程为：

(1)

(2)

(3)

2) 能量守恒方程

p·div(U)+φ+Si

(4)

其中：

3) 质量守恒方程

(5)

4) 气体状态方程

p=ρRT

(6)

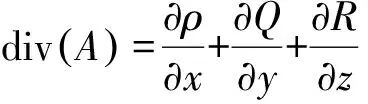
以上6个方程包括3个速度分量的动量方程、1个能量守恒方程、1个质量方程和1个气体状态方程和待求的6个未知数(3个速度分量及压力、温度和密度)数目是相等的，加上相应的初始条件和边界条件即可求解。

2 风挡及舱盖系统原始几何模型及建模

风挡及舱盖的三维模型如图1所示。

图1 风挡及舱盖模型

根据风挡及舱盖的三维模型可看出其为对称分布，因此以脊线为分析曲线，取29个数据点，建立Gambit模型曲线，如图2所示。

图2 脊线上的点的示意图

计算区域的确定：对于流体计算，理论上要求计算区域的尺寸远大于模型的几何尺寸，实际应用中一般取10倍以上的模型几何尺寸。本模型的几何尺寸在X方向为0～5 631.7 mm，在Y方向为-371～1 365.348 952 mm，因此取计算区域为：X方向-80 000～80 000 mm，Y方向-39 000～39 000 mm，并以此建立流体计算模型，如表1所示。

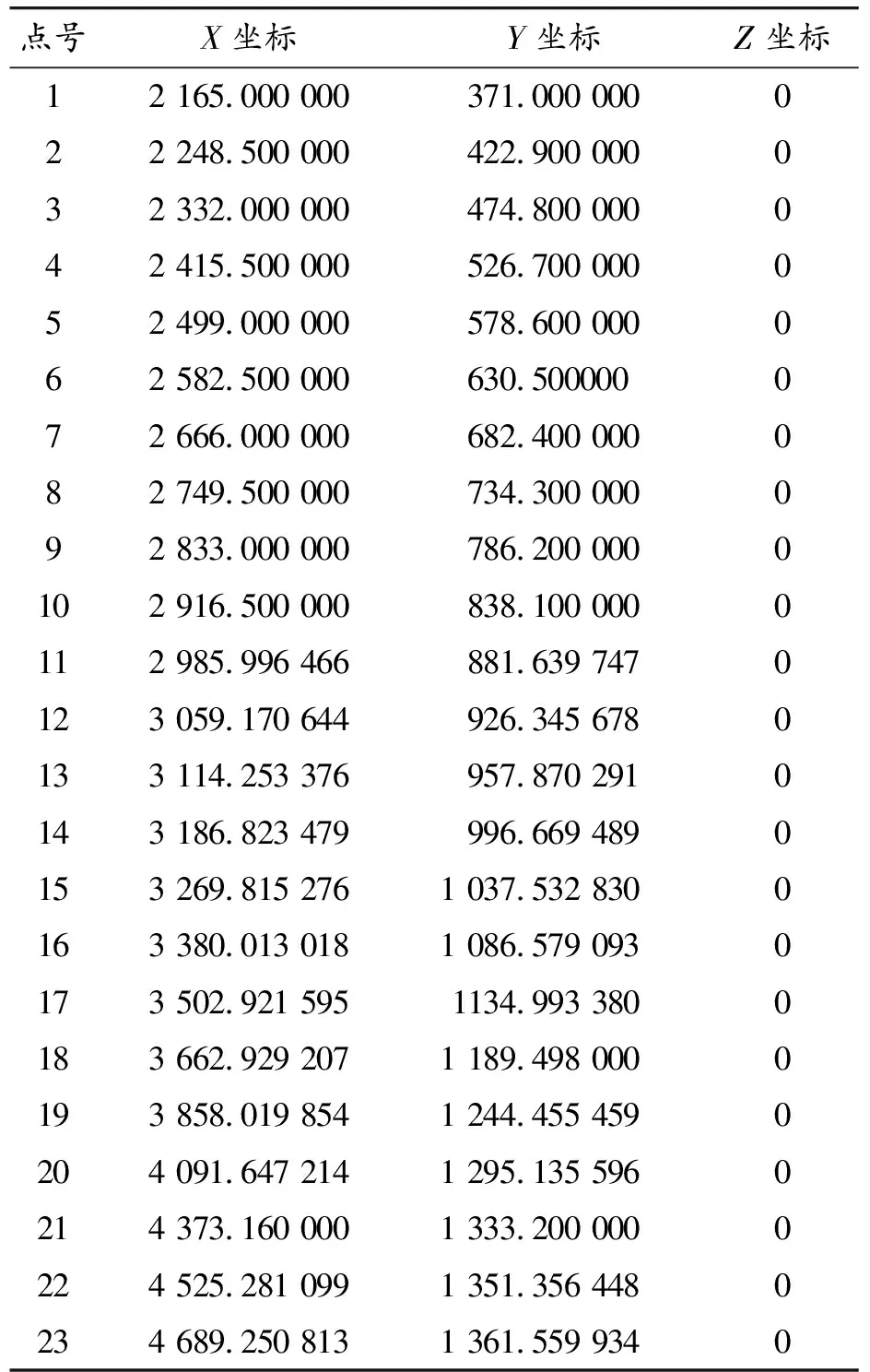
表1 脊线上点的初始坐标值 mm

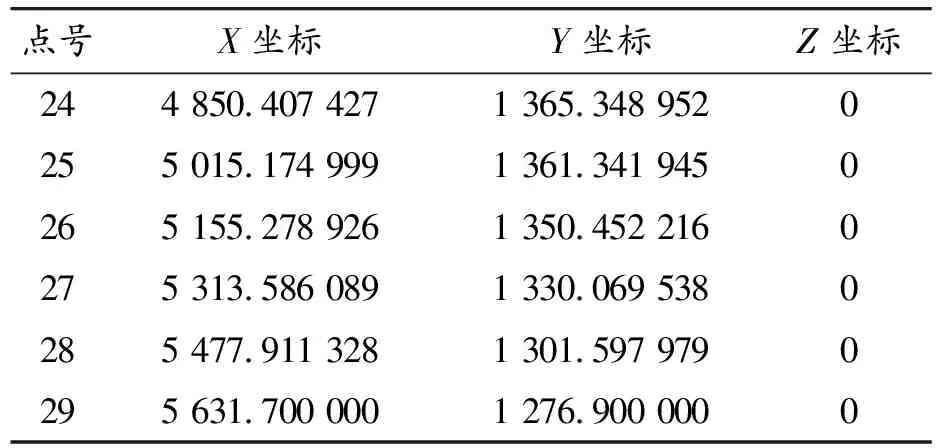
续表1

进行气动计算，还需要对上述脊线模型进一步处理：一是要建立一个封闭的结构体系，二是飞机的前半部分的几何形状对风挡及舱盖系统的气动性能影响较大，因此还必须建立大致的机头模型。由于没有现成的机头模型可以利用，因此对机头作一个简化：将机头部分看成是一个圆锥体，在气动分析模型中对应的就是一个三角形；然后将机头和风挡舱盖体系一起建立一个封闭的气动分析。风挡及座舱的几何造型通常是不规则的光滑曲面，由于其厚度较风挡薄，故通常设计为单层均匀厚度壳体，并且分为前后两个部分，对称分布，因此采用二维建模，如图3所示。

图3 封闭的气动分析模型

对于飞机的封闭模型，本文关心的重点是风挡和舱盖上的气压和温度分布，而对于飞机下部分的几何造型，它对风挡与舱盖上的气压和温度分布影响很小，因此本文不做考虑。整体计算模型如图4所示。

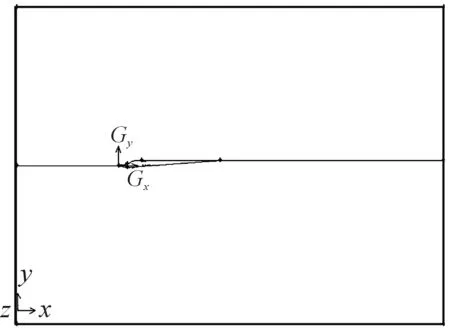
图4 流体计算区域及整体计算模型

在计算区域确定之后，对计算模型进行网格划分，依据流体计算网格划分要求对整体模型划分网格，如图5所示。

图5 流域网格划分

由实际情况，将图5中的左边边线(inlet-1)和下方边线(inlet-2)定为速度输入边界，将右边边线(outlet-1)和上方边线(outlet-2)定为气压输出边界，将风挡与舱盖系统(wall-1、wall-2、wall-3)定为固壁。在完成边界条件的定义之后，将Gambit二维网格以FLUENT 5/6格式导入到FLUENT二维计算求解器中进行气动分析。

3 风挡与舱盖系统气动性能分析

选择耦合-隐式模式下的带热传导方程的Spalart-Allmaras湍流模型求解器进行求解。因为本问题是高速的流场计算，所以采用耦合的求解器和隐式求解器收敛速度较快。流体材料属性设定为标准气体(ideal-gas)，其黏度采用Sutherland定律，由于本问题考虑的工作压强流动速度为0.95马赫数，所以取工作压强为0 Pa，利用求解器求解：设置求解的松弛系数为0.9，迭代误差均选择默认的1.0×10-3，在迭代1 481次时，迭代收敛，此过程的残差曲线如图6所示。

图6 迭代残差

此时的风挡及舱盖系统表面的流域气压分布图、流域温度分布图和流域速度分布分别如图7～9所示。

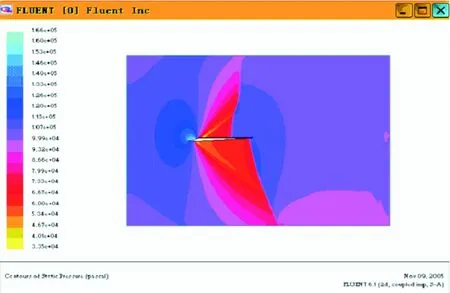
图7 流域气压分布

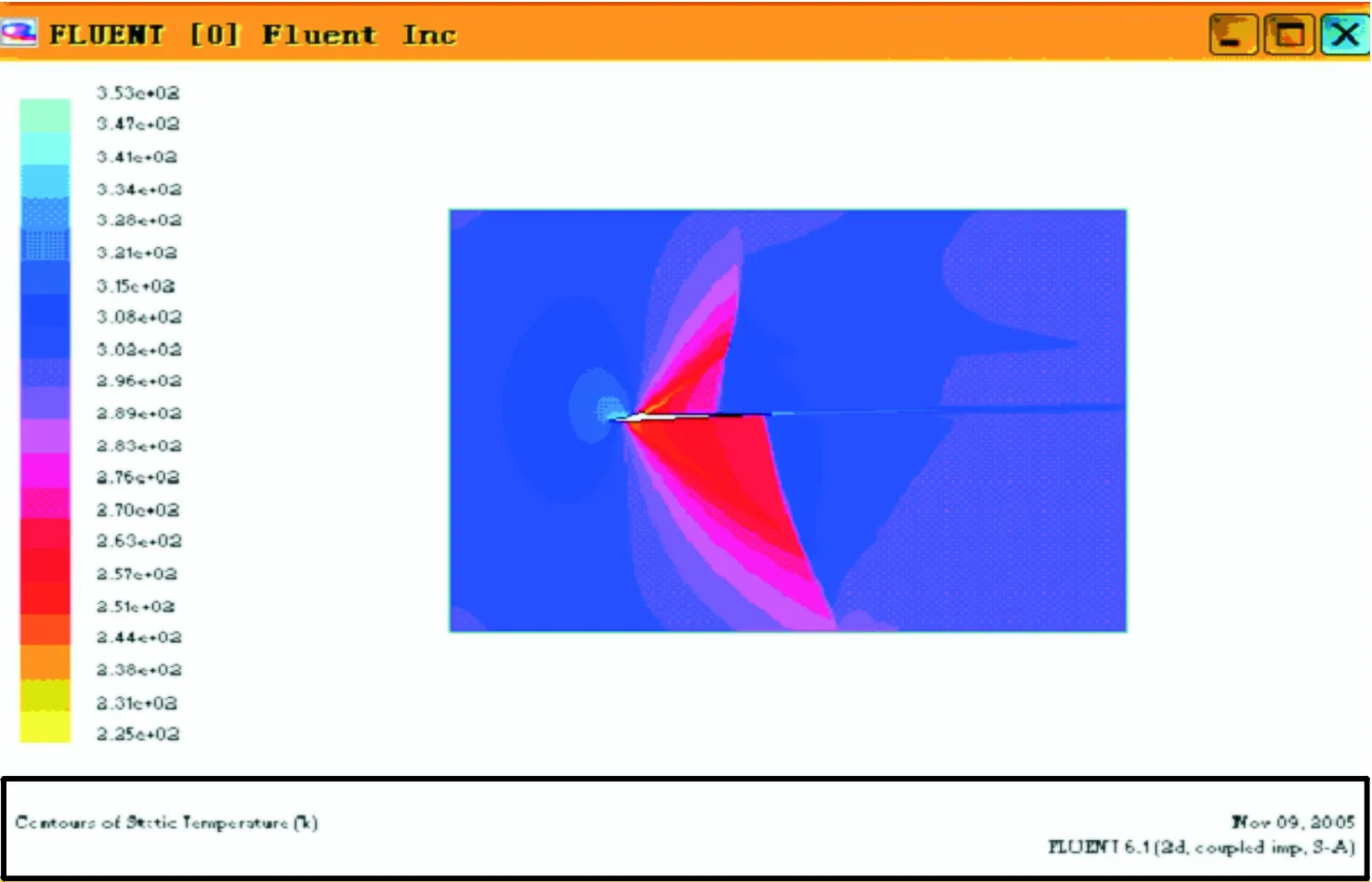
图8 流域温度分布

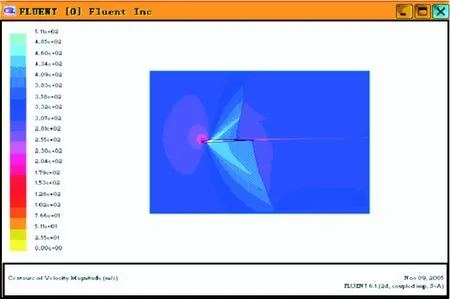
图9 流域速度分布

将计算所得的气压值与所给的试验数据对比，得到脊线上的点的气压值对比，如表2所示。

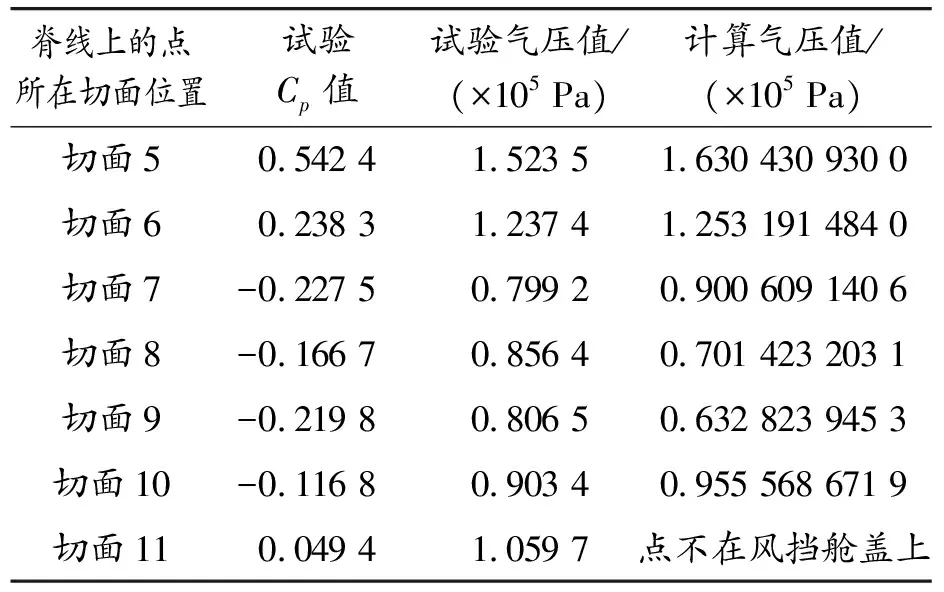
表2 气压结果对照表

4 讨论

从图7～9可以看出，利用这种气动分析模型计算得到的结果比较符合理论分析情况，但从气压结果对照表2可看出，在靠近风挡的位置与试验结果吻合较好(第5、6、7、8、9切面位置)，误差为1.26%；而在靠近舱盖尾部的位置(切面10)的计算结果与试验数据有一定的误差，其主要原因有3点：

1) 由于机头的模型与真实机头模型有一定的差别，导致在风挡上所取的切面位置(第5、6、7切面)的计算气压值比试验数据大。

2) 飞机舱盖后续结构对舱盖上的气压值有一定影响，而在本模型中无法考虑后续结构，因此导致后舱盖上的计算数据比试验数据小，特别是切面10位置的数据偏差很大。

3) 来流方向实际情形应与X轴有一个夹角，但是在本模型计算时，直接采用沿X方向的气流计算，这对风挡舱盖上的整体气压分布有一定影响。

虽然以上模型计算得到的气压值与试验数据在某些位置有一定的误差，但是从对照表2中可以看出：除了切面11之外，只有切面5、6的气压值大于一个标准大气压，即只有切面5、6是压力面，在这2个压力面上，计算得到的气压值比试验数据大，即压力计算偏大，这对于风挡及舱盖设计是安全的、保守的。在吸力面的位置(切面7、8、9、10位置)，只有切面7位置的计算气压值比试验数据大，这表明在切面7 的位置计算吸力比实际吸力小，不安全，但是误差比较小，其他吸力面的计算数据比试验数据都小，表明在切面8、9、10 的位置计算吸力比实际吸力大，这对于风挡及舱盖设计也是安全的、保守的。对于切面7位置，由于在处理试验数据时，取了f=1.5的安全系数，这能够允许我们在计算气压值时存在切面7处的误差。

由此可见，计算模型得到的结果可以用于工程实际设计计算。