初中数学教学中运用“数形结合”的几点体会

江苏省靖江市新港城初级中学 毛丽萍

数形结合方法在初中数学教学中是一个重要的教学思想，同样的也是分析问题、解决问题、处理问题的根本方法和根本策略，学生通过灵活地运用数形结合的方法，能够将一些定律和定理公式直观地描述出来，能够使抽象的问题变得具体化，模糊的数学问题变得清晰可见，提高学生对初中数学的学习积极性和学习效率。运用数形结合方法解决问题时还需要结合实际生活，注重指导学生通过理解和应用来培养学生主动探究的意识，提高初中数学的教学质量。

一、激发学生在初中数学中运用“数形结合”的兴趣

数形结合的重要思想在初中数学教学中一直贯穿到结束，因此教师在日常的数学教学中，就应该合理地融入数形结合的思想教育方法。这样做不仅能够提高初中数学课堂的教学效率，还可以突显数形结合的优越性，激发学生在初中数学学习中运用数形结合教学方法的兴趣，让学生养成良好的习惯。初中生在理解问题，运用数学基础理论和作图工具的过程中，就可以指导学生用数形结合的方法来理解公式，解决数学难题。能够通过培养数形结合的解题习惯，有效地提升学生的意识，从根本上节省学生答题所用的时间。

例1：如果已知长方体的长、宽、高分别是6、8、10，求长方体的体积。这样的问题解决的时候，学生就可以利用数形结合的教学方法画出一个长方体来，直接观察长、宽、高，知道后直接相乘就是长方体的体积。例2：已知平行四边形的两条边长分别是15、20，并且两条边长的夹角是60度，求该平行四边形的面积。教师就可以激发学生运用数形结合解决数学问题的兴趣，让学生画一个平行四边形，然后标出两个边长，再标出夹角的大小，利用直角三角形的相关原理就可以求出平行四边形的高，然后就可以求出该平行四边形的面积。例1，例2的图形如下图：

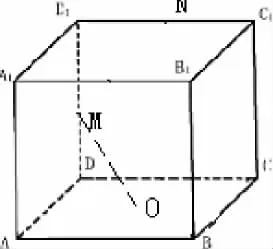
二、培养学生在初中数学中运用“数形结合”的意识

数形结合是一种极其丰富的数学信息转换，可以使抽象思维和形象思维互相穿插着运用。数形结合方法可以使复杂的问题变得简单化，可以使抽象的问题变得具体化。在初中数学教学中，运用数形结合的学习方法，可以用解析问题的方式来说明问题的精确性，能够把握住问题的细节，促使学生解决数学问题的时候能够降低错误率。教师在初中数学课堂中，可以培养学生运用数形结合学习方法的意识，要让学生反思解决问题的方法，运用特殊技巧和解决数学问题时灵活性的思维转换方式来画出图形，并解决问题。通过培养学生的数形结合意识，可以有效地提高初中数学课堂的教学效率。

例如：这样的题目就可以利用数形结合的方法来解决。“一批衣服，每天的销售件数是可知的，进价和售价之差是一天的盈利额，如果降价一点，就需要多卖出点衣服来盈利，需要计算降价多少才算合理 ”这样的问题很显然必须通过题干来整理出需要求的方程式，最后所求的方程式是一元二次方程，学生就可以画一个一元二次方程的图形来直观地解决问题。画一元二次方程图形的时候，学生可以求出方程的对称轴和方程的两个零点，通过这样的方法，只看图形都可以得出结论。因此数形结合解决问题非常简单，拥有了这样的意识对学生来说更加重要。图形如下：

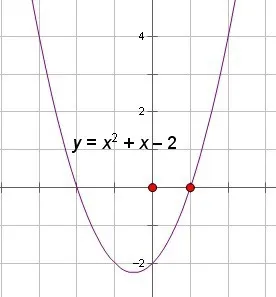
三、引导学生在初中数学中使用“数形结合”的自主性

初中阶段的数学教学，有大部分内容是概念和公式，概念和公式对于学生解决数学问题有着重要的影响。因此，教师要求学生记忆一些常用的初中数学公式是很有必要的。但是有些公式比较复杂，而且学生也记忆困难，给学生的理解和认知方面带来了难题，耗费了学生大量的精力和时间。教师就可以教会学生数形结合的教学理念，让学生自主地去探究是否可以通过运用数形结合的解题思路来得出结论。教师在教学过程中还需要把数量关系和图形结合起来，让学生能够灵活地转化“数”与“形”，能够巧妙地运用数形结合的教学方法来解决数学问题，节省时间。

例如：教师在给学生讲解三角函数的时候，就需要学生通过数形结合的思路来记忆各个三角函数的特征。三角函数的相关公式、概念转化、知识运用都比较复杂，教师如果仅仅依靠概念性、抽象性地对学生讲解三角函数的知识点的话，显然是完全不够的，容易使学生造成混淆。教师就可以利用三角函数的图形来记忆，正弦函数和余弦函数归为一类，利用函数图像来记忆可以减轻学生的负担，同时也可以促进学生的记忆，有效地提高教师的教学效率。利用数形结合的方法还是需要引导学生进行自主探索，自主创新来获取更多的知识。正弦三角函数和余弦三角函数图形如下图：

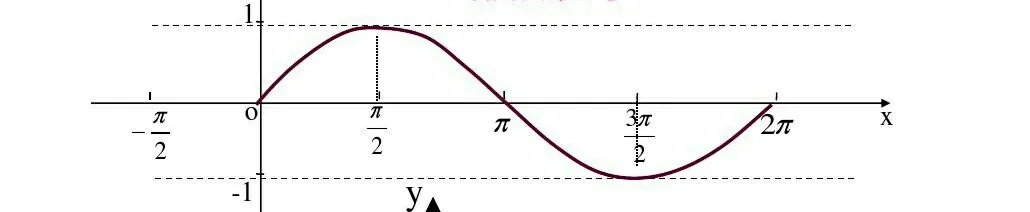
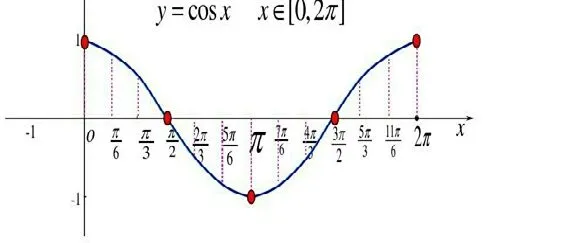
总之，在初中学习阶段，实施数形结合的教学方法，可以有效地提高学生的理解能力，同时加深学生对知识印象的探究能力。教师需要把数形结合的重点放在解决二次函数问题和解决代数问题的时候，因为运用数形结合的方法表述出来，在解决问题的时候就会变得简单一点。运用数形结合的方法来解决代数问题的时候，还可以优化学生的理解，加强学生对题目的认知能力，有效地提高学生学习数学的综合能力。