轴向磁场作用下Czochralski浅液池内热对流特性研究
高 键,彭 岚,马 力,朱承志
(重庆大学动力工程学院,低品位能源利用技术及系统教育部重点实验室,重庆 400044)
1 引 言
在Cz法制备晶体的过程中,熔体在温差梯度作用下会产生表面张力梯度,形成Marangoni-热毛细对流。当温差梯度超过某一临界值后,熔体流动将转变为非稳态振荡流动,其会使晶体的均匀性受到破坏、影响晶体材料的生长质量[1]。近几十年来,学者们对不同工质[2-3]、不同几何模型[4-5]、不同边界条件[6-8]下的熔体对流运动进行了大量的研究,得到了热毛细对流的演变规律,并分析和解释了相应的物理机制。Teitel等[9]对Cz液池内流动不稳定性进行了研究,考虑不同内外径之比对流动的影响,发现增大内外径之比可以减小临界温差。Peng等[10]对Cz浅液池内硅熔体的热对流过程进行了深入的研究,发现随着径向温差的不断增大,流动会发生由稳态流动向非稳态流动的转变,并确定了流型转变的临界条件。
施加外部磁场是抑制熔体热对流的一种行之有效的方法。Virbulis等[11]采用二维轴对称模型,研究了稳态磁场、交变磁场和复合磁场对熔体对流对界面形状的影响,并与实验数据进行了比较。Ozoe等[12]对磁场作用下矩形池内的热对流进行了三维数值模拟,研究结果表明:磁场方向对熔体的对流运动具有较大的影响,当外加磁场方向垂直于竖直边界层时,抑制效果最强;而当外加磁场方向平行于竖直边界层时,抑制效果最弱。Takagi等[13]研究了在水平温差作用下,坩埚旋转和轴向磁场对熔体热毛细对流的影响。结果发现:单独施加磁场和同时施加磁场和旋转均对流动具有较好的抑制作用。
目前对磁场作用下熔体热对流的研究主要集中在由单向水平温差引起的流动,而在Cz法生长单晶硅的过程中,由于熔体温度较高,易与外界进行辐射换热、引起散热损失;同时,生产中对坩埚底部进行加热,均会导致垂直自由表面方向产生相当大的温差梯度[14]。故在实际工程应用中,双向温差梯度往往同时存在,共同驱动流体进行运动。因此,本文采用数值模拟方法对Cz液池内Marangoni-热毛细对流进行研究,保持底部热流密度恒定,主要讨论了轴向磁场对临界水平温差Macri、稳态流动和非稳态流动的影响。
2 物理数学模型
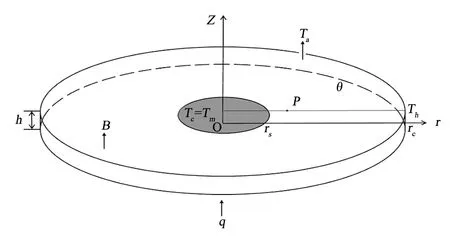
图1 物理模型Fig.1 Configuration of system
物理数学模型如图1所示,晶体半径rs=15 mm,坩埚半径外径rc=50 mm,圆柱形坩埚半径内充满了深度h=3 mm的硅熔体。坩埚侧壁和熔体-晶体界面分别维持恒定温度Th和Tc,水平温差ΔT=Th-Tc。熔体表面与外界进行辐射换热(环境温度:Ta)。坩埚底部以均匀的热流密度q进行加热,并沿Z轴正方向施加磁场强度为B的静态磁场。
为简化计算,作以下假定:(1)熔体流动速度较低,可考虑为层流;(2)熔体为不可压缩牛顿流体;(3)除自由表面以外,其他界面均满足贴壁无滑移条件;(4)自由表面考虑热毛力作用,其与温度满足线性关系;(5)边界都为电绝缘。
根据上述假设,无量纲化基本方程如下:
▽·V=0
(1)

(2)
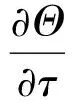
(3)
式(2)中F为洛伦兹力,其无量纲分量如下:
(4)
(5)
FZ=0
(6)
其中,φ为电势,满足下列方程式:
▽2φ=▽·(V×B)
(7)
无量纲化边界条件为:
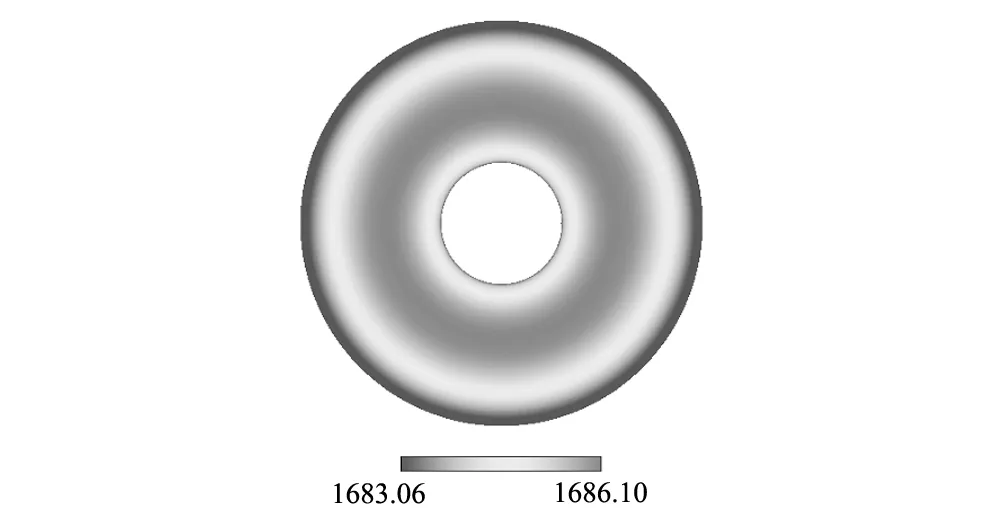
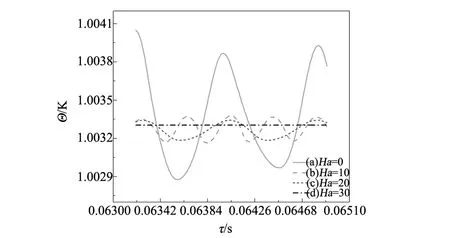
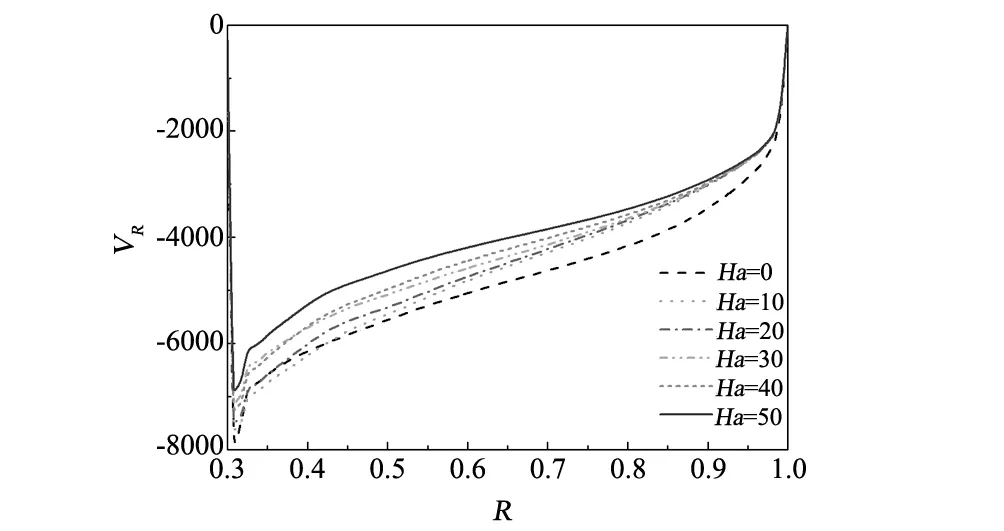
自由表面(Z=h/rc,rs/rc (8) 液池底部(Z=0,0 (9) 熔体-晶体界面(Z=h/rc,0 (10) 坩埚侧壁(0 (11) 利用有限容积法对控制方程进行离散,压力插值采用PRESTO格式,对流项为QUICK格式,扩散项为中心差分格式,压力-速度修正采用PISO算法,程序的正确性验证参阅文献[14]。在Ma=1185,Q=1.5705×10-2工况下分别对不同大小的网格进行了计算,结果如表1所示,采用80R×120θ×40Z非均匀交错网格。 表1 网格无关性检验Table 1 Grid independent test 由于硅熔体熔点温度较高,易与外界环境进行辐射换热。为了避免因热量损失导致硅熔体温度下降而形成结晶,在坩埚底部施以恒定热流密度对熔体进行加热。图2给出了底部热流为Q=1.3461×10-2(q=3 W/cm2)时自由表面温度分布情况。此时,熔体的最低温度不低于晶体的熔点温度1683 K,确保了物理模型的合理性。故本文保持底部热流密度恒定(即Q=1.3461×10-2),重点考察磁场强度和水平温差梯度对熔体传热和流动过程的影响。 当水平温差较小时,液池内硅熔体的流动将保持轴对称稳定状态,这种流动被称为基本流。图3 给出了Ma=2370(ΔT=12 K)时,自由表面监测点P处温度和速度随时间的变化关系,此时监测点温度和速度都不随时间而变化,熔体内Marangoni-热毛细对流为稳态流动状态。为了进一步了解磁场强度对这种稳态流动的影响,定义自由表面温度波动δΘ为: 图2 Ma=0(ΔT=0 K),Q=1.3461×10-2时,自由表面温度分布Fig.2 Ma=0,Q=1.3461×10-2,free surface temperature distribution 图3 Ma=2370(ΔT=12 K),Qmin=1.3461×10-2时,监测点P处温度和速度变化Fig.3 Ma=2370,Qmin=1.3461×10-2,variations of temperature and velocity at the monitoring point P 图4给出了不同Ha数下自由表面温度波动情况。当磁场强度较低时(0≤Ha≤20),此时Ha值较小,波型结构保持不变,为直条幅波;当磁场强度增加到Ha=30时,磁场对流动结构具有显著的抑制效果,波型由直条幅波演化成椭圆状波,波数由12减少到4;随着磁场强度进一步增大(40≤Ha≤50),由于此时流动强度已十分微弱,导电流体在磁场作用下产生与流动方向相反的洛伦兹力,其数值也相对较小,磁场对流动的抑制效果逐渐减弱,自由表面温度波动结构和波数不再发生变化。 图4 Ma=2370(ΔT=12 K),Q=1.3461×10-2时,不同Ha数下自由表面温度波动情况Fig.4 Ma=2370, Q=1.3461×10-2, free surface temperature fluctuation 随着水平温差不断增大,液池内硅熔体流动强度将进一步加剧。当Ma超过临界Macri时,流动会发生失稳,此时监测点P处的温度可呈现出周期性的等幅振荡,如图6(b)所示。一个振荡周期内最高温度和最低温度的差值即为温度振幅,其与Ma呈近似的线性关系[15]。利用线性外推法可确定不同磁场强度作用下流动转变的临界Macri。图5给出了当底部热流Q=1.3461×10-2,Ha数分别为0、10、20和30时,监测点P处的无量纲温度振幅A与Ma数之间的变化规律。 表2给出了相应条件下临界Macri和线性拟合公式。可以看出,在保持底部热流密度恒定的情况下,随着轴向磁场不断增强,临界Macri不断增加且变化幅度愈来愈大,说明轴向磁场的引入会提高Marangoni-热毛细对流的稳定性。 表2 Q=1.3461×10-2时不同Ha数下的临界水平温差MacriTable 2 Critical Ma with different Ha when Q=1.3461×10-2 图5 Q=1.3461×10-2时不同Ha数下监测点P处温度振幅A与水平温差Ma的关系Fig.5 Change of the temperature amplitude A with Ma at the point P for different Ha when Q=1.3461×10-2 图6 Ma=3950(ΔT=20 K),Q=1.3461×10-2时,不同Ha数下监测点P处温度变化Fig.6 Ma=3950, Q=1.3461×10-2, temperature evolution at the monitoring point P for different Ha 图7 Ma=3950(ΔT=20 K),Q=1.3461×10-2时,不同Ha数下自由表面温度波动情况Fig.7 Ma=3950, Q=1.3461×10-2, free surface temperature fluctuation 由表2可知,在没有轴向磁场的作用下,当Ma>3385.3时,流动为非稳态振荡对流。为了研究轴向磁场对非稳态流动的影响,对水平温差Ma=3950(ΔT=20 K)时,不同Ha数下的熔体流动进行了一系列数值模拟。图6给出了自由表面监测点P处温度随时间的变化情况,从图中可以看出:当磁场强度为零时(Ha=0),温度振荡混乱而无规律;随着磁场强度不断增大(10≤Ha≤20),温度呈现规律的等幅振荡,但流动仍保持三维非稳态状态;当Ha=30时,此时Ma数已小于对应磁场强度下的临界Macri,温度振幅减小至零,流动由非稳态转变为稳态。 图7所示为Ma=3950时,不同磁场强度下自由表面的温度波动图。当未施加轴向磁场时(Ha=0),自由表面温度波动为一种典型的热流体波,呈现出弯曲的轮辐状;引入轴向磁场后(10≤Ha≤20),流动的不稳定性逐渐减弱,温度波动由原来的热流体波转变为叉状结构;当Ha=30时,自由表面呈现出明暗相间的直条纹,波动结构由三维非稳态流动过渡为三维稳态流动,波数m=11;随着磁场强度进一步增大(40≤Ha≤50),此时磁场对流动的影响较小,与图4中的计算结果类似,温度波动结构基本保持不变,但自由表面波数先减小后增大。 图8 Ma=3950(ΔT=20 K),Q=1.3461×10-2时,不同Ha数下自由表面径向速度分布Fig.8 Ma=3950,Q=1.3461×10-2,radius velocity distributions on free surface 图8给出了Ma=3950时,不同磁场强度下自由表面熔体径向速度分布图。从图中可以看出,最大无因次径向速度出现在靠内壁面附近。随着磁场强度的不断增加,径向速度沿径向分布的非线性程度不断减弱,速度分布曲线愈加平缓。当Ha=0时,最大无因次径向速度为7490.67;而Ha=50时,最大无因次径向速度为6850.74,最大无因次径向速度随着磁场强度的增加而不断减小,表明洛伦兹力对熔体流动的具有显著的抑制效果。 表3给出了水平温差Ma=2370、3950(ΔT=12 K 、20 K),熔体在Ha数为0、10、20、30、40、50下,自由表面最大温度波动值。从表中可以看出,轴向磁场对稳态和非稳态Marangoni-热毛细对流均有抑制作用,当磁场强度Ha=30时,自由表面最大温度波动值呈数量级递减,此时磁场对流动的抑制效果最为明显。随着磁场强度进一步增大(40≤Ha≤50),自由表面最大温度波动值变化幅度逐渐减弱,这是因为此时熔体流动已较为微弱,磁场对流动的抑制效果也逐渐减弱,这与图4和图7中自由表面温度波型结构的演变过程相吻合。同时也可以看出,在磁场强度保持一定的情况下,随着水平温差梯度的增加,自由表面最大温度波动值不断增大,熔体内部流动也更为剧烈。 表3 不同Ha数下Ma=2370、3950时自由表面最大温度波动值Table 3 Maximum temperature fluctuation value with different Ha when Ma=2370, 3950 本文采用三维数值模拟方法研究了轴向磁场对双向温差作用下Czochralski浅液池内Marangoni-热毛细对流的影响,主要讨论了轴向磁场对临界Macri、稳态流动和非稳态流动的影响,结果表明: (1)在底部热流密度恒定的情况下,确定了不同Ha数下流动由三维稳态向三维非稳态转变的临界Macri。随着Ha数的增大,临界Macri不断增大,轴向磁场的引入会增强Marangoni-热毛细对流的稳定性。 (2)轴向磁场对液池内稳态和非稳态Marangoni-热毛细对流均具有较好的抑制效果。对于稳态流动,磁场的引入会使自由表面温度波动幅值受到削弱,波数减少;对于非稳态流动,随着磁场强度的不断增加,监测点P处的温度振荡逐渐减弱直至消失,流动由三维非稳态转变为三维稳态,自由表面温度波动结构发生显著变化,波动幅值逐渐下降。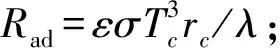

3 结果与讨论
3.1 轴向磁场对稳态流动的影响


3.2 轴向磁场对临界Macri的影响



3.3 轴向磁场对非稳态流动的影响

4 结 论

