发展高中生数学高阶思维的几点思考

☉重庆市江津中学校 兰 勇

很多教师往往会将大量的习题训练当作数学高效学习的重要途径，但实际上，问题解决过程中的思维才是数学高效教学必须重点关注的，高效的思维方式才是教师在课堂教学中应该始终关注的.

一、注重思维的深刻性

就题解题只是学生在认识问题的初级阶段的思维变现，学生对问题形成深刻的理解才是教师高效教学应该追求的，学生对问题的理解能够达到由此及彼、由表及里直至去粗取精、去伪存真的境界才能说明学生对问题真正理解了.

例1将函数的图像向左平移φ个单位，所得的图像对应的函数为偶函数，则φ的最小正值是______.

分析：将函数的图像向左平移φ个单位，得求φ的最小正值.

方法1：偶函数的对称轴为x=0，即y轴，把x=0代入得或2，则或-1，故，所以φ的最小正值为

方法2：由题意为偶函数，故有恒等 式化 简 得.因为sinx不恒为0，因此0，故，以下同上.

方法3：直接作函数的图像，如图1，观察图像可知，将图像向左平移个单位长度即可.

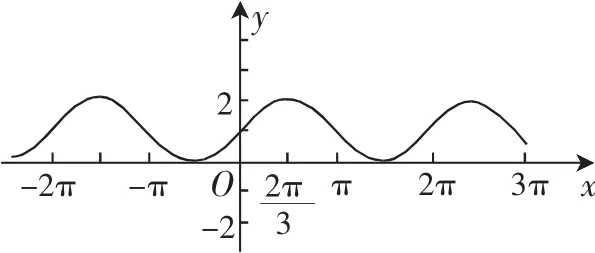
图1

问题圆满解决，那么此题是否还有更值得思考的地方呢？函数图像的上下移动其实就是函数值的改变，图像的形状、单调区间等并没有发生变化，所以，将函数y=视为考查对象就可以了.

二、注重思维的简洁性

透过复杂的现象进行本质的把握能令解题者更好地抓住主要矛盾并做到思维上的删繁就简.

例2函数f（x）=|x2-4|+x2+kx（x∈R）的单调减区间为（-∞，-2），则k的取值范围为______.

分析：有的学生往往受导数处理函数单调性的思维定势的影响会联想到用导数来解决本题，那么解决此题必须这样吗？首先，去绝对值符号可得

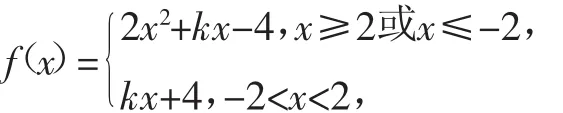
所得分段函数由一次函数与二次函数组成，那么，此处要用导数知识来解决吗？

其次，“函数f（x）的单调减区间为（-∞，-2）”这一条件又应该怎样理解呢？将题目理解为如下意思是否可以：已知（-∞，-2）为函数f（x）=|x2-4|+x2+kx（x∈R）的单调区间，k的取值范围如何？答案是否定的，原题想表达的是（-∞，-2）为函数f（x）的单调减区间，且函数f（x）只在这一区间上为单调减函数.结合函数图像可知，对称轴在［-2，2］之间，于是且k＞0，解得0＜

突破“复杂”的重围并让思维变得简洁是思维的高级阶段，“简单”与“复杂”的对比往往更具有价值.

三、注重思维的严谨性

思维的严谨性表现在学生对知识的“知其所以然”上.

例3已知函数若对于任意的x1∈R均存在x2∈R，并令g（x2）=f（x1），则实数a的取值范围为______.

分析：g（x）=sin4x-cos4x=-cos2x∈［-1，1］.由条件易知函数f（x）的值域应为函数g（x）值域的子集.f（x）的定义域为R，因此接下来应求函数f（x）的值域.

思路1：对x进行分类讨论.

当x=0或a=0时，f（x）=0.

当x＞0时

若a＞0，则

若a＜0，则

当x＜0时

若a＞0，则

若a＜0，则

思路2：运用导数知识.

这两种思路相对于这样一道中等水平的填空题来说较费笔墨.观察函数f（x）解析式的结构特点并联想基本不等式a2+b2≥2ab（a，b∈R）的加强形式a2+b2≥2|a||b|（a，b∈R），可以这样求解函数f（x）的值域：

若a=0或x=0，则f（x）=0，符合题意；

当a≠0且x≠0时

显而易见，此种思路更加简洁而高效.由此可见，思维变得严谨不仅能对自己解题中的思维过程进行充分的认识，还能使解题者根据问题的要求及时调整思维的方向与解题的手段，当然，解题者的主动反馈是这一过程中必不可少的.

四、注重思维的敏捷性

不被情景性的暗示所左右、不迷信权威并敢于向权威提出质疑是思维敏捷性、独立性的表现.数学思维的敏捷性更多地表现在运算环节与推理过程的缩减上，与概括性紧密关联的敏捷性又在概括与推理的“立即”上有所展现.

跳出一般的解题框架并结合问题的条件、结论、背景提出自己独创的见解是解题者思维敏捷性的表现，一般来说，想象力丰富的学生往往更容易获得独创性的解法.

例4已知函数，则以下结论不正确的是______.

（1）∀x∈R，等式f（-x）+f（x）=0恒成立；

（2）∃m∈（0，1），使方程|f（x）|=m有两个不等实根；

（3）∀x1，x2∈R，若x1≠x2，则一定有f（x1）≠f（x2）；

（4）∃k∈（1，+∞），使得函数g（x）=f（x）-kx在R上有三个零点.

分析：很多题目中往往具有看似比较简单的情境，解题者往往也会因为情境的简单而误以为这是一道简单题，思维与解法往往也就因此误入歧途了.对于命题（1），似乎只要联想奇偶性的定义就可以顺利解决，那么从数的角度进行推理论证是否也可以解决下面的命题呢？

显然不行.对下面三个命题进行仔细观察不难发现，利用图像判断的意味还是相当明显的，因此，若将函数的图像作出就可以顺利解决问题了，如图2所示.

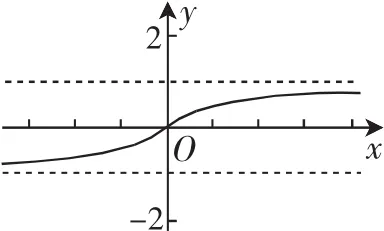
总之，高中数学教师可以借助问题来指导学生，使学生的思维能够在由此及彼、由表及里的思考中变得更为深刻，在删繁就简、把握本质的解题中变得更为简洁，在知其所以然的探索中变得更为严谨，在触类旁通的推理与论证中变得更为敏捷，只有令学生的思维方式变得更加灵活才能保障数学学习的高效性.W