高中数学教学中如何提高学生的思维能力

☉江苏省如东县马塘中学 徐皓亮

在高中阶段的数学学习中，对学生的思维能力的要求比较高.反过来讲，学习数学能够对学生的思维能力以及思维发散能力进行锻炼.所以，在进行学习的过程中，要注重对学生思维方面的培养以及锻炼.在平时的授课时，老师应当在培养学生逻辑思维的同时，加强对学生的想象能力、运算能力以及判断能力的锻炼.如果在平时的教学过程中忽视了对学生思维能力的培养，就会让学生觉得学习数学非常的困难，甚至厌烦数学.以致于在课堂上不注意听讲，在课下也不会对数学知识进行复习，从而造成学生的数学成绩下降的后果.在当前时代发展阶段，对于学生的数学思维能力提出了更高的要求，因此，老师要更加注重学生思维的培养.

一、什么是数学直觉思维

数学直觉思维的定义是人的大脑对于数学的相关概念以及理论能够很好的理解，能够更容易地进行领悟.人类的思维方式能够分成直觉思维方式和逻辑思维方式两种.人们之前都在试图将这两种思维方式分开来看待，认为两者之间是没有任何联系的.这种看法以及观点是不对的.人的两种思维方式之间的关系是密不可分，相互依赖的.刚开始数学概念的产生就是人们先在脑海中形成一个想法，然后通过论证才形成的.在不断地发现问题然后对发现的问题进行解决的过程中才形成了数学.所以在发现问题时离不开人的直觉，也离不开逻辑思维能力.在给学生进行知识讲解的同时，教师应当将自己的思维能力展现出来，这样，学生才能够了解教师的思维，才能在此基础上进行深入的思考.比如在对证明题进行练习的时候，假如教师只是按照步骤将证明的解题过程呈现给学生，学生只能学习到这道题目的解题方法，如果将题目转换一下，学生就解不出来了.因此在进行讲解的时候，老师需要将解题的思维讲给学生，调动学生学习的积极性，引起学生的学习兴趣，让学生能够深入地理解题目，这样才能够让学生抓住题目的本质，做到举一反三.例如，在讲解函数奇偶性时，要将一类题型进行变式训练，将奇偶性与函数单调性结合起来.

例1已知函数f（x）是偶函数，而且在（0，+∞）上是减函数，判断f（x）在（-∞，0）上是增函数还是减函数，并证明你的判断.

变式1下列函数中，在其定义域内既是奇函数又是减函数的是（ ）.

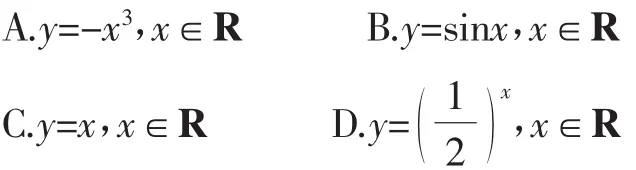
解：分别画出四个函数的图像，如图1所示.

B项在其定义域内是奇函数但不是减函数；

C项在其定义域内既是奇函数又是增函数；

D项在其定义域内是减函数但不是奇函数.

故选A.

变式2函数y=f（x）是R上的偶函数，且在（-∞，0］上是增函数，若f（a）≤f（2），则实数a的取值范围是（）.

解：当a＞0时，因为函数y=f（x）是R上的偶函数，且在（-∞，0］上是增函数，所以y=f（x）在（0，+∞）上是减函数，所以若f（a）≤f（2），则a≥2，当a＜0时，函数y=f（x）是R上的偶函数，且在（-∞，0］上是增函数，且f（-2）=f（2），所以a≤-2.故选D.

二、直觉思维的特点

（一）简约性

对比于逻辑思维来讲，直觉思维相对来说比较容易，它不需要学生进行推理判断，但是具有一定的跳跃性，需要有一定的经验以及知识储备，以便对对象进行全面的考查.并且直觉思维需要有一定的想象力来构建出假设，它是瞬间思维，是人的灵感的体现，需要人们自己进行领悟以及发掘.其过程相对来讲更加的简单，但是却能够比较清楚地发现事物的本质.如考查函数的抽象运算与综合性质时，首先要先分析题目的立意，考查的是哪方面的内容，然后通过直觉思维进行解题.

例2如图2所示，fi（x）（i=1，2，3，4）是定义在［0，1］上的四个函数，其中满足性质“对［0，1］中任意的x1和x2，任意λ∈［0，1］，f［λx1+（1-λ）x2］≤λf（x1）+（1-λ）f（x2）恒成立”的只有（ ）.

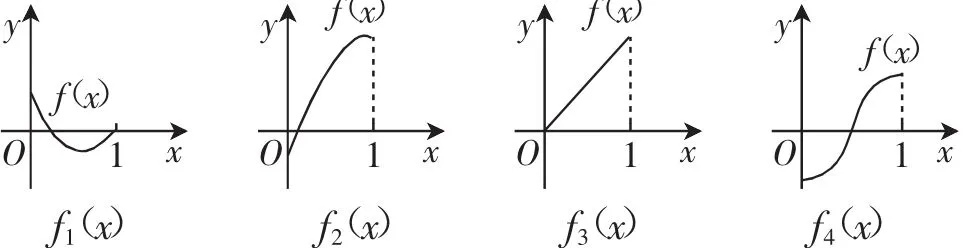
图2

解：特殊值法，当时，符合条件的函数是凹函数或一次函数，从图像可看出只有符合题意，故选择A.

（二）创造性

当今时代，科技在快速的发展，社会的进步需要更多的人才，并且，要求人才所具备的能力也越来越高.所以，学校需要培养出能够满足社会需求的人才，必须对学生的创造能力以及创新能力进行培养.在我国更加注重培养与发展学生的逻辑能力，学校对于学生知识的考查是以课本为基础的，要求学生掌握课本的知识，然后运用到试卷当中就可以了，这就让学生在学习时按部就班，做很多练习题.但是，这对于学生创新能力的培养是非常不利的.直觉思维要求学生能够将思维进行发散，而不是一成不变的接受，所以在对学生的思维进行培养时，要注意培养与发展学生的创新能力.

（三）自信力

从一般情况来看，学生学习一门课程，喜爱这门课程的原因主要体现在以下两个方面：第一，是喜欢教课的老师，为了引起老师的注意，努力学习这门课程.第二，是对于学科本身的喜爱程度比较大.对于数学这门课程来讲，笔者发现大部分的学生喜欢数学在很大程度上都是出于对数学学科本身的喜爱.如果一个人能够不断的获得成功，那么这个人就会变得越来越自信.而自信就会让人们更加注重自己的直觉性.当人们不用依靠理论推理而是直接用直觉就可以解决一个问题时，会带给别人震撼.这就会让学生更加愿意去学习，进而培养自己的直觉性.

三、怎样培养学生的直觉思维

数学思维的能力以及人们的直觉性会对人们的判断能力产生一定的影响，换句话来讲，直觉能力的大小与人们的思维能力的大小有着直接的关系.学生的数学直觉能力不是在出生的时候就定了，在学生的学习生活中是可以对学生的直觉能力进行培养的.随着人们见识的增加，学习的知识的增多，人们的直觉思维能力也在不断的发展.

1.数学直觉的产生并不是偶然的，也不是随机就可以获取的，它需要先具备扎实的基础.直觉的产生是在原来的基础上进行的假设，并不是随意的猜测臆想.所以，假如没有扎实的基础作为支撑的话，也就没有很高的直觉思维能力.

2.渗透数学的哲学观点及审美观念.在直觉产生之前，需要对研究对象总的情况进行全面地了解以及掌握，运用哲学能够有利于人们看清事物的本质.数学的本质是能够发现事物的逻辑规律，并且要求主体具有美的意识.所以，对于哲学知识的学习有助于对数学思维的培养.

3.选取适宜的题目类型.在进行数学学习的时候，老师要选择比较典型的题目让学生进行练习，这样可以让学生的思维能力得到更好的锻炼.采用开放性的教学模式对学生直觉思维的培养是非常有利的.这是由于开放性的教学模式能够让学生从多个角度对问题进行思考，而并非从一个角度进行分析.

4.设置直觉思维的意境和动机诱导思维观念.在进行讲课的时候，教师就该明确地提出直觉思维的概念，并且鼓励学生进行思维的培养.对问题进行全面的分析，在这个过程中注重学生思维的培养.比如，在进行运算时可以采用换元法或者采用数形结合法进行解题.这样，能够让学生重视对思维能力的培养.

四、结语

对数学直觉思维方面的锻炼是长时间的过程，并非短期就可以完成的.所以，在平时的教学过程中，老师应当注重将这方面的培养纳入到教学计划当中，让学生对问题进行深入的分析、全面的探讨、积极的思考，从而使学生的思维能力得到有效的提升.W