城市信号交叉口左转车流车头时距分布特征研究
温惠英, 曾钰宸, 李 硕
(1.华南理工大学 土木与交通学院,广东 广州 510641; 2. 湖南大学 土木工程学院,湖南 长沙 410082)
0 引 言
道路交叉口作为城市道路的瓶颈,制约着整个城市道路网通行能力。目前,国内外学者对城市信号控制道路交叉口(以下简称“信控道路交叉口”)的交通特性做了大量研究,其中以直行车道和右转车道居多。根据M. A. MAREK[1]的研究,74%道路交叉口交通事故的发生与左转车辆相关。因此,对左转车道研究至关重要。
国外对左转车道研究相对成熟,但多集中于饱和流率和通行能力方面以及侧重于根据道路交叉口几何条件、车道布置形式、横向干扰、以及车辆跟驰模型等方面对给定基本交通流率或通行能力进行修正。关于道路通行能力计算,文献[2]采用的是修正系数法;文献[3]采用的是经验系数法;文献[4]采用的是韦伯斯特公式计算方法;其他各国则多在文献[2]基础上根据本国实际情况对参数进行修订。
车头时距是交通流率和道路通行能力研究的根本依据,但在传统车头时距分布模型(如移位负指数分布、韦布尔分布、爱尔朗分布、M3分布模型[5]等)出现后,该方面的研究成果主要体现为根据不同影响因素对分布公式参数进行修正。例如:R.T.LUTTINEN[6]对不同等级公路进行了对比,发现不同限速的公路,车头时距在一定范围内分布相同;D.A.NOYCE等[7]将左转车道许可型信号相位和保护型信号相位下各项交通特征进行了比较;R.W.STOKES[8]则对道路交叉口不同车道宽度、进口道和白天、夜间行驶条件等各组因素进行对比。
国内学者对信控道路交叉口车头时距也有一定研究。邵长桥等[9]确定了信号道路交叉口饱和车头时距启动延误车辆值;赵星等[10]研究了不同跟驰模型对饱和车头时距的影响;段力等[5]对不同交通密度下的饱和车头时距进行了研究;杨晓光等[11]则综合考虑了各影响因素对饱和流率的影响。针对左转车道,YANG Zhao等[12]对设立了左转待行区的交通影响进行了评价;宗二凯[13]和林栋[14]分别对信控交叉口不同布置形式下的左转车道通行能力进行了研究;王炜等[15]则主要针对无信号控制道路交叉口进行分析。
总体而言,我国学界对信控道路交叉口左转车道车头时距分布模型研究较为有限,且鲜有考虑高峰和非高峰时段车头时距分布差异特征。在未来城市智能交通中,该差异是反映交通特性[16]、建立冲突延误模型[17]进而调整信号配时方案[18]的重要依据,因此我国在信控道路交叉口左转车辆车头时距系统性研究亟需完善。
若采用文献[2]、[19]等常规方法对左转车流饱和车头时距进行预测,其结果往往偏大;采用4种传统车头时距分布模型和SPSS的9大基本曲线模型,其拟合效果也不理想;故需要重建车头时距分布模型。笔者以大中型城市典型信控道路交叉口左转车道车头时距分布为研究对象,分别在饱和和复合状态下对比其高峰、非高峰的信控道路交叉口左转车道车头时距分布特征,从而建立相关统一的分布模型,并与文献[2]、[19]等通用算法进行对比。
1 车头时距数据采集
信控道路交叉口车头时距数据采集主要分为人工记录和仪器检测两类。出于左转车辆行驶状况复杂考虑,仅采用现场按秒表易产生较大随机误差;从设备技术层面考虑,超声波、红外线、雷达和检测线圈均存在一定程度系统误差。故笔者采用人工与仪器结合方法,通过录像法记录完整信控道路交叉口左转车道交通状况,然后分别在各周期内按车辆通过停车线次序,采集全部左转车辆车头时距并进行人工统计输出,由此获取较为可靠的试验数据。
调查地点为长沙市的典型CBD交叉口芙蓉中路—人民中路交叉口,该交叉口的西、南、东这3个进口道左转车道均为含待行区,并设有保护型信号相位左转专用车道,调查过程分别对高峰和非高峰两个时段进行录像采集。
根据统计学原理[20],以饱和车流特征为标准,确定了城市信号交叉口左转车道启动延误车辆值[9],从而得到复合状态下车头时距分布数据;在此基础上对行车安全距离理论[21]和饱和状态连续性条件进行筛选,最终获取了饱和状态下车头时距数据。笔者将以此实测数据为基础,分别建立饱和状态和复合状态下城市道路信控交叉口左转专用车道车头时距分布模型。
筛选所得数据选取合适组距进行分组并绘制相应频数分布,以饱和状态高峰时段为例,所得车头时距分布见图1~4实测值。
2 分布特性分析
由于饱和状态下高峰与非高峰时段在峰值车头时距及分布集中程度均存在一定差异。笔者将分别从饱和和复合状态、高峰和非高峰两个方面对车头时距分布特性进行进一步对比分析。
2.1 饱和状态与复合状态比较
饱和状态定义为连续通过的一列车队,车辆间车头时距保持不变的稳定状态。文中复合状态则为城市信控道路交叉口中绿灯开启后车流达到稳定状态下的正常行驶情况,区别在于未进行饱和车头时距阈值限定,能更为全面体现车头时距分布,更符合实际情况。
根据实测数据,对比不同状态下车头时距分布可看出:
1)平均车头时距:从实测数据和模型分析可看出,复合状态下信控道路交叉口左转车辆平均车头时距在高峰和非高峰两个时段均比饱和状态大,其主要原因是复合状态中间断流产生车头时距波动范围较大。
2)集中程度:通过对比饱和状态和复合状态车头时距分布,可知这两者都存在较为明显的集中情况,且反映在同一范围内。当车头时距为1.500~2.500 s时,饱和状态分布概率接近60%,其中高峰时段为59.8%,非高峰时段为57.5%;复合状态下也达到了50%以上,其中高峰时段为52.4%,非高峰时段为51.2%。可见饱和状态与复合状态车头时距相比集中程度较高。
2.2 高峰时段与非高峰时段比较
对比不同时段车头时距分布可看出:
1)总体而言,信控道路交叉口左转车道高峰时段交通流率比非高峰时段大。
2)超过1/4的车头时距集中于2.000~2.500 s(其中饱和状态下约为31%,复合状态下约为27%),其集中程度较高,但峰值车头时距暂时依靠实际观测统计值确定,理论值仍需进一步探讨。
3)高峰与非高峰两个时段内50%以上的车头时距均集中在1.250~2.750 s;非高峰时段车头时距集中程度较高峰时期小,说明其在较小车头时距的概率分布集中程度(交通密度)要大于高峰时期。出现该现象可能存在3点原因:① 非高峰时段比高峰时段车流更为平稳,受驾驶员个人习惯影响较大,易反映为较稳定的平均水平上;② 高峰时段相对非高峰时段影响因素较多,驾驶环境更为复杂,加之驾驶员处于上下班途中,心理状况较为紧张,故可能发生的驾驶状态也相对复杂,因此高峰时段车头时距概率分布较为分散;③ 高速行驶过程中,驾驶员为保持安全距离易不自觉放大车头时距,因此出现高峰时段车头时距偏大情况。
3 车头时距分布特性模型建立
3.1 传统模型和SPSS曲线模型拟合效果
对信控道路交叉口左转车流在高峰和非高峰时段内的饱和状态和复合状态两种情况下车头时距分布分别进行建模拟合。根据图像的形态特征,选用韦布尔分布、爱尔朗分布和SPSS涉及常见的9大概率分布曲线[22]分别进行拟合,并对模型预测结果和实际观测结果分别进行配对样本t检验。以饱和状态高峰时段为例进行建模拟合(图1、 2),拟合结果系数及模型检验结果如表1。
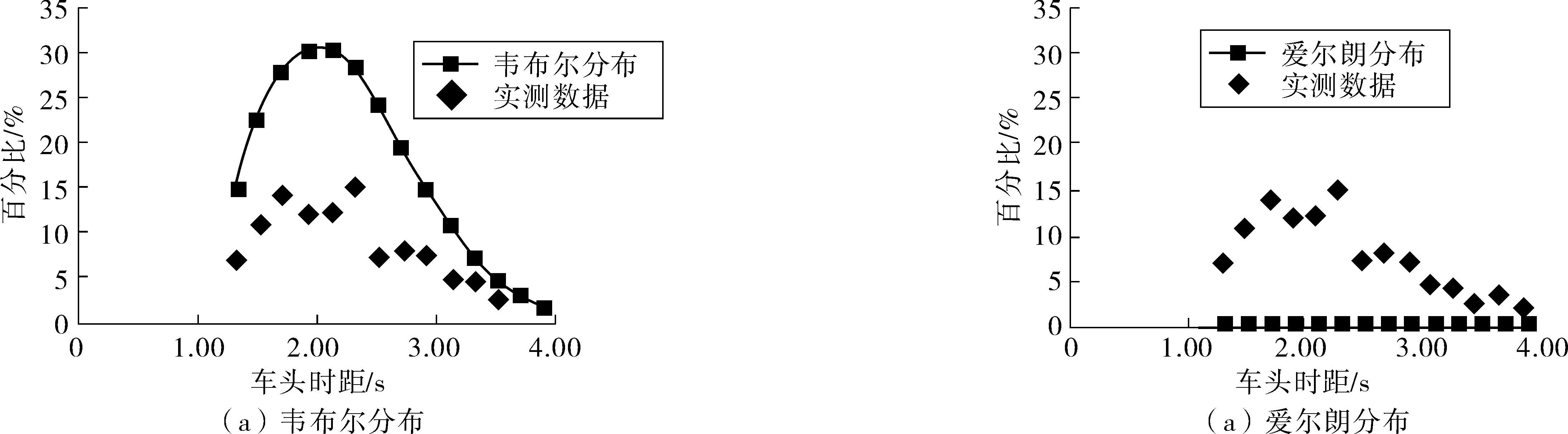
图1 高峰时期分布比较Fig. 1 Comparison of the distribution during peak hours

图2 高峰时段的分布曲线比较Fig. 2 Comparison of distribution curves in peak period

方程式模型摘要R2Fdf1df2显著性常量参数估计值b1b2b3线性(L)0.2803.8881100.07716.830-3.399——对数0.1692.0301100.18513.425-5.997——逆模型(N)0.0710.7641100.4034.7197.835——二次项(Q)0.5966.652290.017-9.21720.258-4.731——立方(U)0.83313.284380.002-77.524116.972-46.3665.551—复合(U)0.3455.2681100.04525.0510.577——幂0.2052.5841100.13914.365-0.964——S0.0890.9821100.3451.2551.281——增长(H)0.3455.2681100.0453.221-0.550——指数分布0.3455.2681100.04525.051-0.550——对数0.3455.2681100.0450.0401.733——
从图1、2可看出:韦布尔分布基本形态与实测数据概率分布最为接近,但其增长速度和峰值幅度都与实测值存在一定差距;在该交通流率下,爱尔朗分布则无法捕捉到产生分布峰值的准确位置,其基本形态与实际分布有较大偏离。至于9大基本概率分布曲线,除二次函数及三次函数外,其余模型均忽略了峰值出现,但上述模型在4.000 s左右均出现反向增大现象,显然不符合常理,需进一步研究。
3.2 分段函数拟合模型建立
笔者采用分段函数分别建立饱和状态和复合状态下的统一模型,探讨高峰和非高峰时段的车头时距分布特征。
3.2.1 饱和状态
在不同分组情况下,笔者分别对分段函数的两段模型拟合结果进行分析。先将SPSS通过曲线拟合初步得出的R2与F检验进行大概判断,选出满足要求的几类模型;再将这几个种类选中,在SPSS中进行ANOVA检验[22],得出各类型所有参数,依次按照R、F和t检验的优先顺序进行筛选比对,得出不同分组情况下满足要求的函数模型。其中高峰时段上升段和下降段的备选模型分别如表2;最后通过图像形态确定最终理想模型。
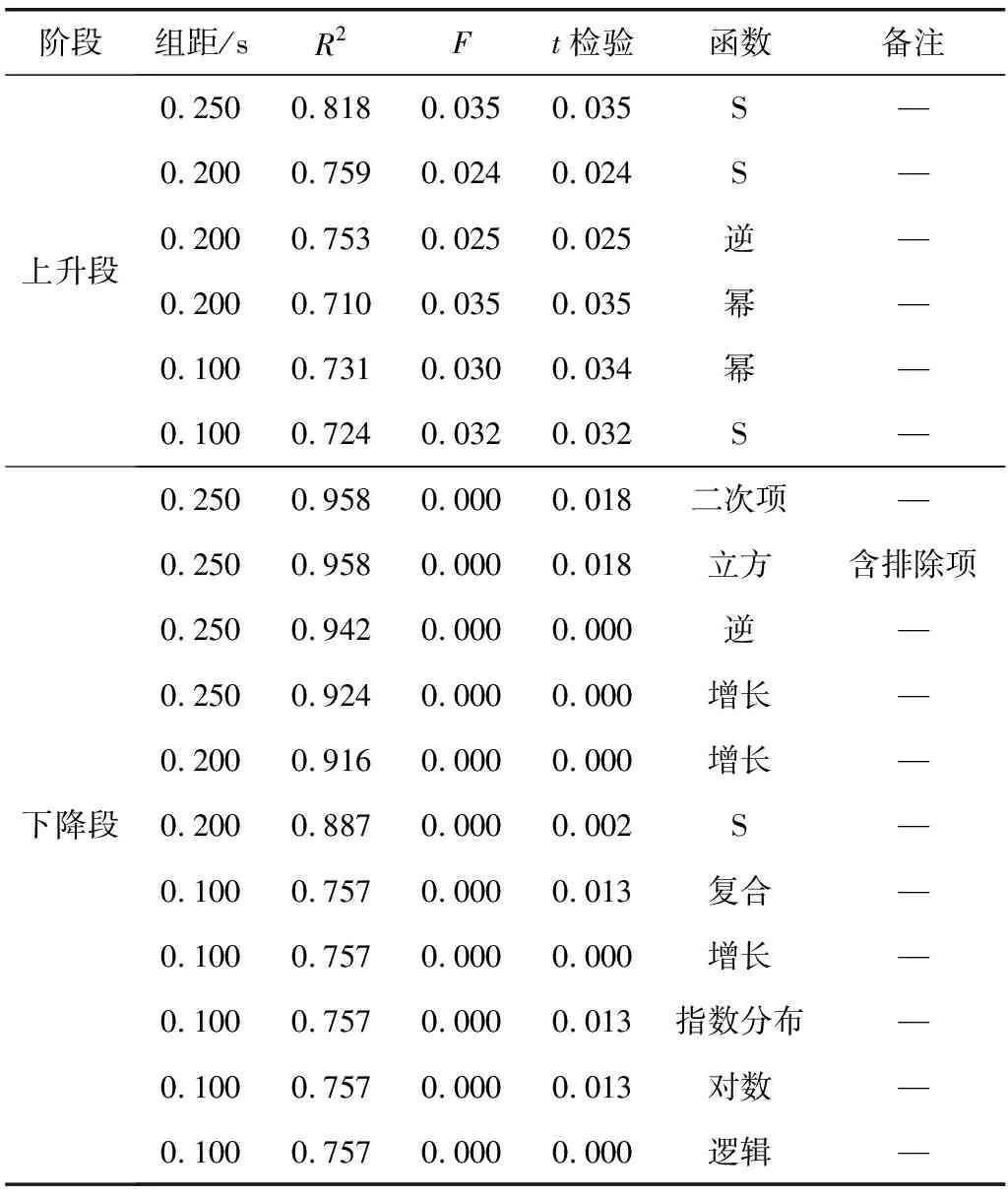
表2 高峰时期上升、下降段备选模型汇总Table 2 Summary of possible models at ascent and decline stageduring peak hours
1)高峰时段
对于上升段,组距为0.250 s时的S模型相关性系数R2最高,R2=0.818,且F、t两种检验均满足要求。因此,可按组距为0.250 s进行S函数曲线拟合,拟合效果见图2(b)。由图2(b)可看出:S概率分布曲线与观测数据十分接近,且满足逐渐上升趋势,符合驾驶员行为习惯,且临界值均在合理范围内,故高峰时段的信控道路交叉口左转车道车头时距分布上升段将采用S概率分布曲线。
对于下降段,组距为0.250 s时的二次函数和立方函数的相关性系数R2均为最高,R2=0.958,且F、t两种检验均满足要求,但由于立方函数含有排除项,准确性难以得到保证。因此,应按组距为0.250 s进行二次函数曲线拟合,拟合曲线与实测值的对比如图3(a)。由图3(a)可见:二者拟合效果较好,但在接近上限时,饱和车头时距分布会出现反向增大的不正常现象,不符合概率分布随车头时距增加而逐渐减缓的下降趋势,故应重新考虑其他模型。
从表2中选择相关性系数其次的逆函数模型。其R2=0.942,F、t两种检验均为0,完全满足0.05的检验水平。因此,可按组距为0.250 s进行逆函数曲线拟合,拟合效果见图3(b)。由图3(b)可看出:概率分布曲线形态与实际相符,且所有预测值均在允许取值范围内,故高峰时期左转车道车头时距分布下降段将采用逆函数模型。
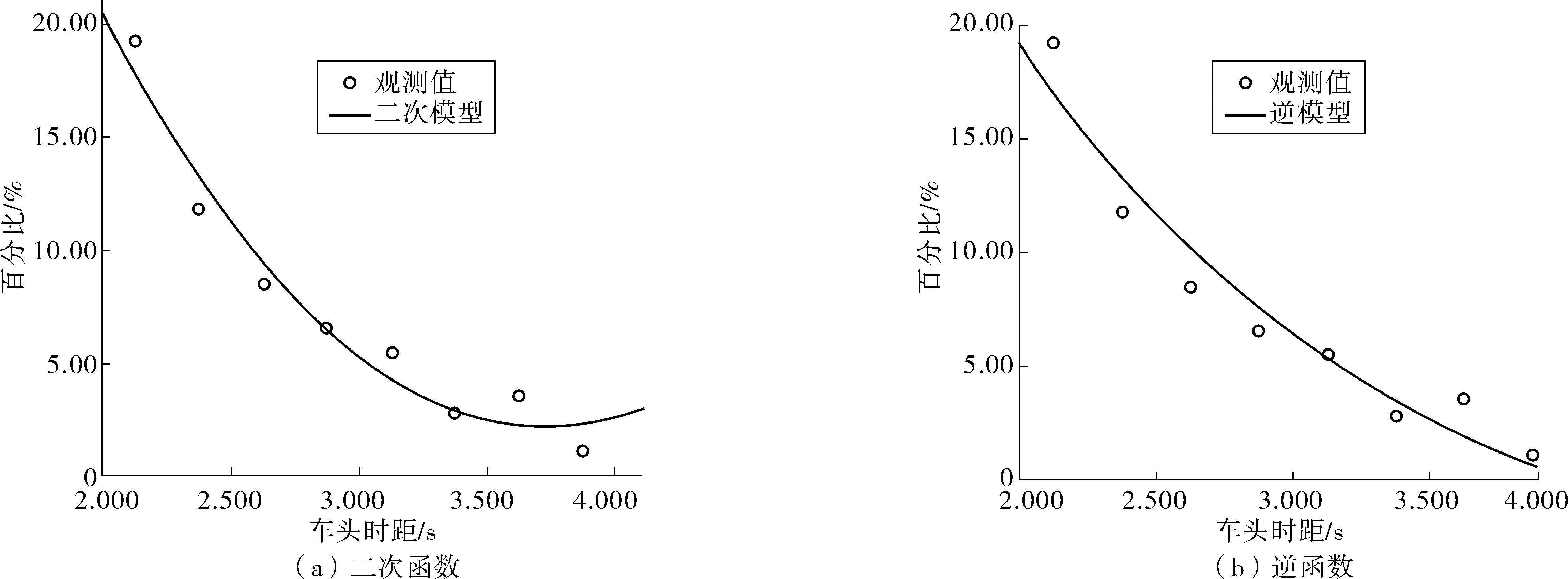
图3 高峰时段下降段函数拟合Fig. 3 Function fitting of descending segment in peak period
由ANOVA检验结果显示:按照组距为0.250 s、上升段(0 拟合计算所得结果见表3。由于两段函数在临界点处出现阶跃,计算结果表明,取二者平均值更加接近实测值。 表3 高峰时期饱和车头时距模型预测Table 3 Prediction of the saturated time headway model during peak hours 根据上述确定的函数类型进行拟合,可得相应的高峰时段信控道路交叉口左转车流车头时距分布模型如式(1): (1) 当t=2.125时,取式(1)的平均值。 2)非高峰时段 根据高峰时段处理方法,同理可得非高峰时段信控道路交叉口左转车道饱和车头时距分布模型,如式(2): (2) 当t=1.900时,取式(2)的平均值。 3)饱和状态下的统一概率分布模型 比较发现,高峰与非高峰时段信控道路交叉口左转车流车头时距概率分布模型的分段函数模型属于同一类型,可通过参数调整实现不同时段车头时距分布描述,故建立统一模型形式如式(3): (3) 当t=Δ时,取式(3)的平均值。 式中:α为度量系数;β为增长系数或集中系数;Δ为峰值车头时距,s;tmin和tmax分别为饱和车头时距下限和上限。 其中:α取值越大,其峰值越大,上升阶段通常取α=4.0,下降阶段取α=-14.0。β取值取决于所处阶段,上升阶段为β=-3.0,取值越大,靠近峰值增长速度越快,集中程度越高,下降阶段则为β=60.0,取值越小,靠近峰值下降速度越快,集中程度越高。 3.2.2 复合状态 根据饱和状态处理方法,同理可得复合状态下高峰与非高峰时段车头时距分布模型。 1)高峰时段 复合状态下高峰时段下信控道路交叉口左转车道车头时距分布模型如式(4): (4) 当t=2.250时,取式(4)的平均值。 2)非高峰时段 非高峰时段的信控道路交叉口左转车道车头时距分布模型如式(5): (5) 当t=1.750时,取式(5)的平均值。 3)复合状态下的统一模型 同理可建立起复合状态下信控道路交叉口左转车道车头时距概率分布函数描述的统一形式,如式(6): (6) 当t=Δ时,取式(6)的平均值。 式中:α、β、Δ的含义同饱和状态。 其中,上升阶段通常α=7.0,下降阶段α=-2.5,取值越大,峰值越大;上升阶段β=1.8,下降阶段β=13.0,取值越大,分布曲线变化速度越快,集中程度越高。 目前左转道路通行能力的计算方法主要有3种:① 根据文献[2],多数情况下一条车道理论通行能力为1 900 pcu/h,通过多项参数修正,计算信控道路交叉口左转车道实际通行能力;② 根据文献[19],设计速度为40 km/h时,一条车道基本通行能力为1 650 pcu/h;③ 根据文献[23],一条车道理论通行能力取1 500 pcu/h较为合理,其专用左转车道设计通行能力可根据左转车辆所占比例求得。 根据上述3种方法所得的道路通行能力,可换算求得相应的车头时距。各种方法计算所得车头时距及其与实测值的对比结果见表4和图4(a),文中模型与实测情况对比见图4(b)。 表4 车头时距计算值与实测值的对比Table 4 Comparisons between the calculated and measured time headway 图4 各计算方法对比Fig. 4 Comparison of different calculation methods 通常情况下,高峰时段交通流量大,车流密度大,车头时距小于非高峰时段。由表4可看出:文中模型计算结果和实测值都反映了这一规律,说明文中模型的合理性。从对比计算结果可看出:文献[2]误差为16.39%,文献[19]误差为26.64%,文献[23]误差为39.34%,而文中模型误差则小于4%。其中高峰时段预测更为准确,误差仅有0.010 s,非高峰时段也不超过0.100 s。由此可见,文中模型与实际情况吻合度更为理想。 由于传统模型适用条件限制,现仅对饱和状态下的车头时距分布进行特性比对。根据韦布尔模型、爱尔朗模型和文中模型可得不同车头时距对应的分布概率。饱和状态高峰时段分布特性与实测情况对比如图5(a),非高峰时段如图5(b)。 图5 饱和状态高峰和非高峰时段概率分布模型对比Fig. 5 Comparison of probability distribution models between peak and non-peak periods in saturated state 由图5可见:爱尔朗模型在相应流率下得出概率分布模型效果最不理想,计算所得函数值与实际情况明显不符;韦布尔模型形态与实际分布存在相似之处,但概率数值和增长速度均大于实际分布情况,无法准确反映曲线取值和在上升、下降过程中的变化速度;文中模型分布形态较为理想,建立饱和状态下左转车道车头时距分布模型与实测情况吻合良好,具有良好参考价值。 笔者通过对信控道路交叉口左转车道饱和车头时距研究,得到如下结论: 1)对城市典型信控道路交叉口左转车流车头时距高峰与非高峰时段分布进行特性分析和对比;在饱和状态与复合状态下分别建立了信控道路交叉口左转车流车头时距概率分布统一模型; 2)笔者建立的分段模型能较好地对车头时距及其分布特性进行预测。目前常用方法对车头时距平均值预测误差通常都超过16%,文中模型误差则低于4%;相对于传统模型,文中模型能较好拟合车头时距实际分布形态,具有较好的参考价值; 3)对比饱和状态和复合状态车头时距分布,发现二者均存在2.000~2.500 s内集中程度最高且超过27%、集中在1.500~2.500 s内超过50%的现象; 4)对比高峰与非高峰两个时段车头时距分布,发现非高峰时段车头时距分布集中程度低于高峰时段,且倾向于集中在较小的车头时距上。 需特别指出的是,文中研究对象为设有保护型信号相位含待行区的左转专用车道,适用于交通流量较大典型城市信控道路交叉口。研究成果对其他类型交叉口适用性有待进一步研究。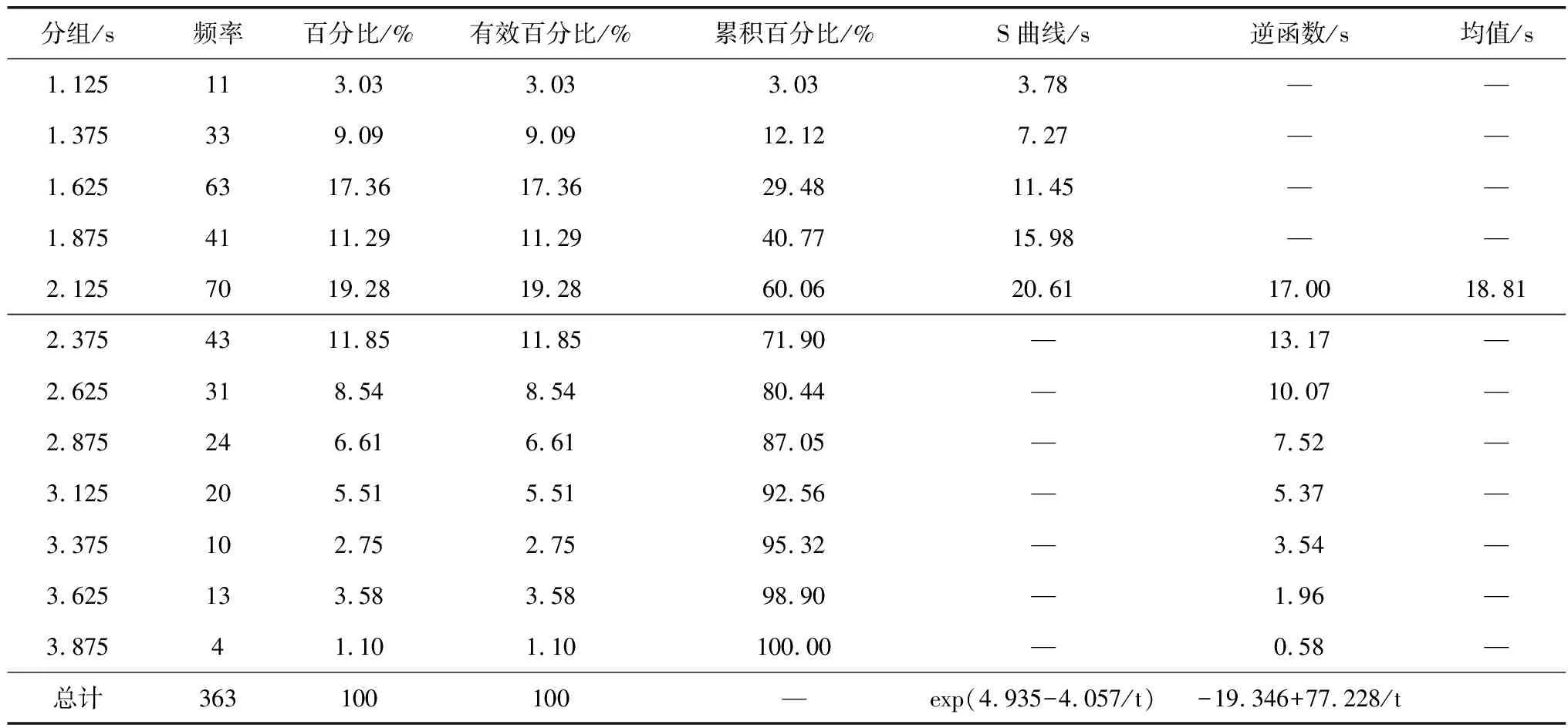
4 模型检验
4.1 与常用方法对比


4.2 与传统模型分布特性对比

5 结 论

