谬误已成觅果因——一道中考数学题的探究与课后反思

宋永明 刘 彦

(山东省东营市胜利第一中学 257027)

探究背景

如图，AB是⊙O的直径，AB=8，点M在⊙O上，∠MAB=20°,N是弧MB的中点,P是直径AB上的一动点，若MN=1，则△PMN周长的最小值为( ).

(A)4 (B)5 (C)6 (D)7

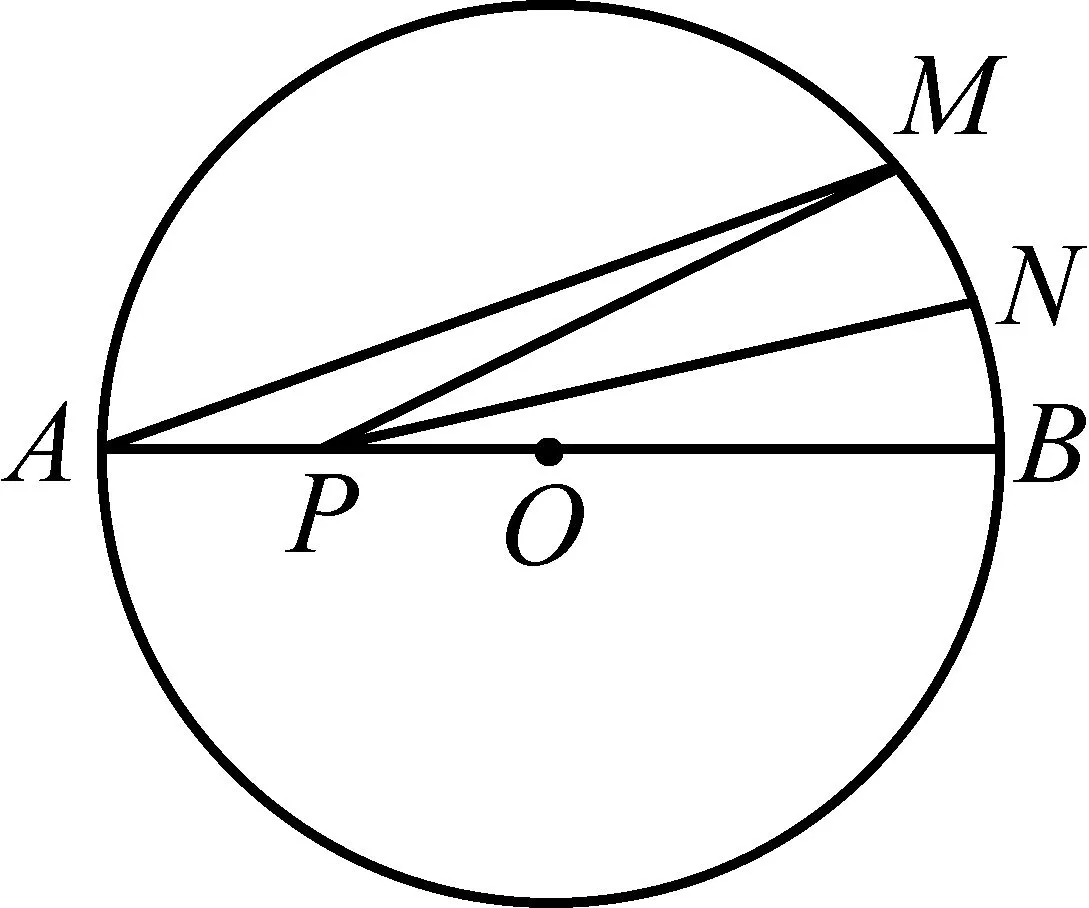
本题是2015年广西南宁中考数学的第11题，这道题笔者要求学生在课堂上当堂完成，结果全班46名同学仅1人完成.究其原因，主要是学生对知识的综合运用能力有待提高.

问题探讨

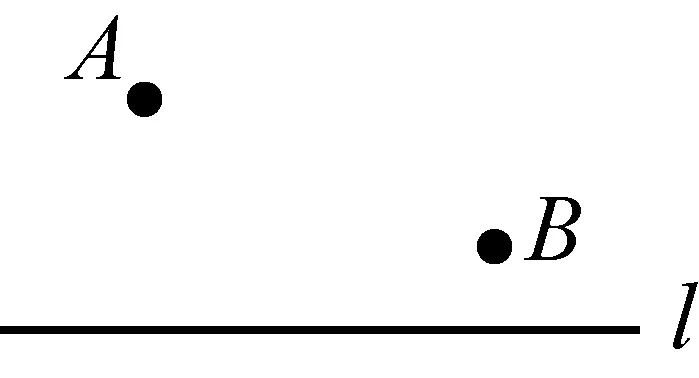
首先让学生进行了旧知回顾. 如下图，问题：在直线l上求一点P，使PA+PB值最小.几乎所有的学生立即给出了问题解答作法：作B关于l的对称点B′，连AB′与l交点即为P．原理：两点之间线段最短．

PA+PB最小值为AB′.

问题解决

本题考查的是轴对称﹣最短路径问题，凡是涉及最短距离的问题，一般要考虑线段的性质定理，结合本节所学轴对称变换来解决，多数情况要作点关于某直线的对称点．

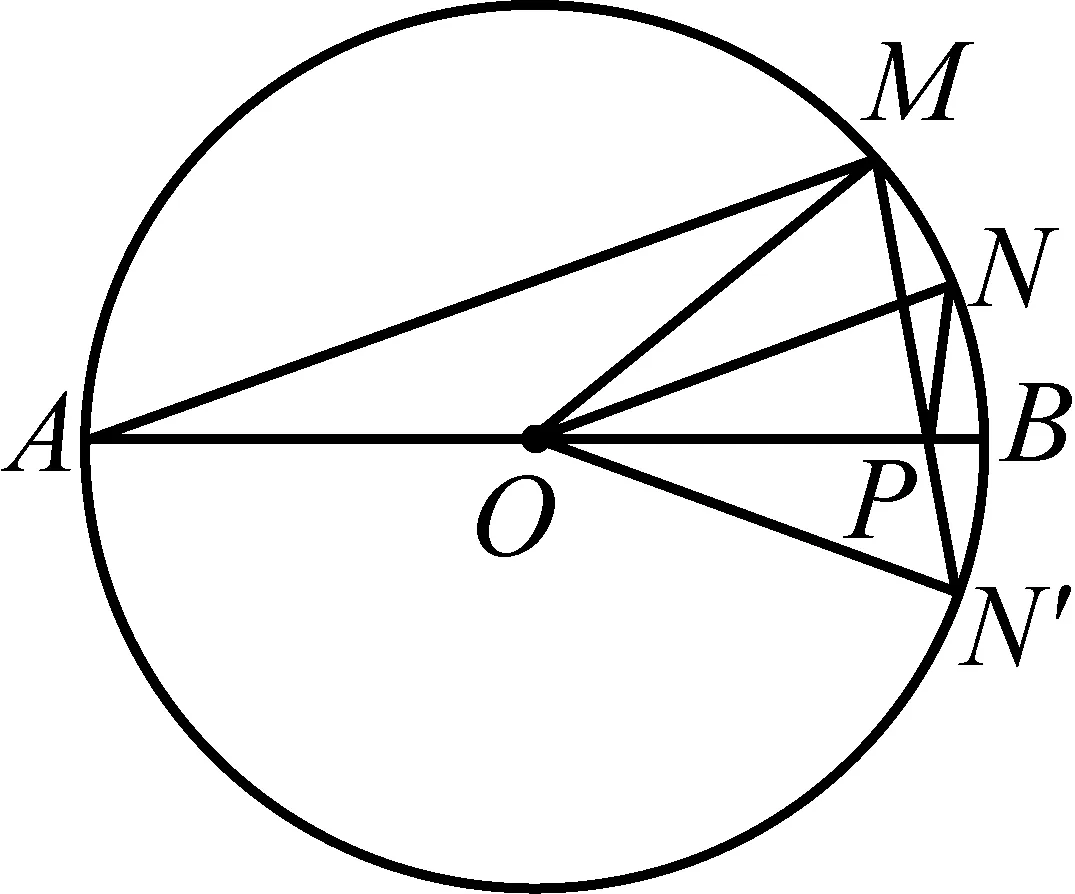
解作N关于AB的对称点N′，连接MN′，ON′，ON．因为N关于AB的对称点N′，所以MN′与AB的交点P′即为△PMN周长的最小时的点，因为N是弧MB的中点，所以∠A=∠NOB=∠MON=20°， 所以∠MON′=60°，所以△MON′为等边三角形， 所以MN′=OM=4， 所以△PMN周长的最小值为4+1=5．故选B．

学生质疑

笔者讲完后，很快有一名学生提出疑问：若P与直径AB上的点B重合时，因为N是弧MB的中点，所以MN=BN=1.

根据三角形三边关系定理：BM<2，所以△PMN周长为1+1+BM,一定小于4.笔者在课上思考后，认为学生的思路正确.

验证

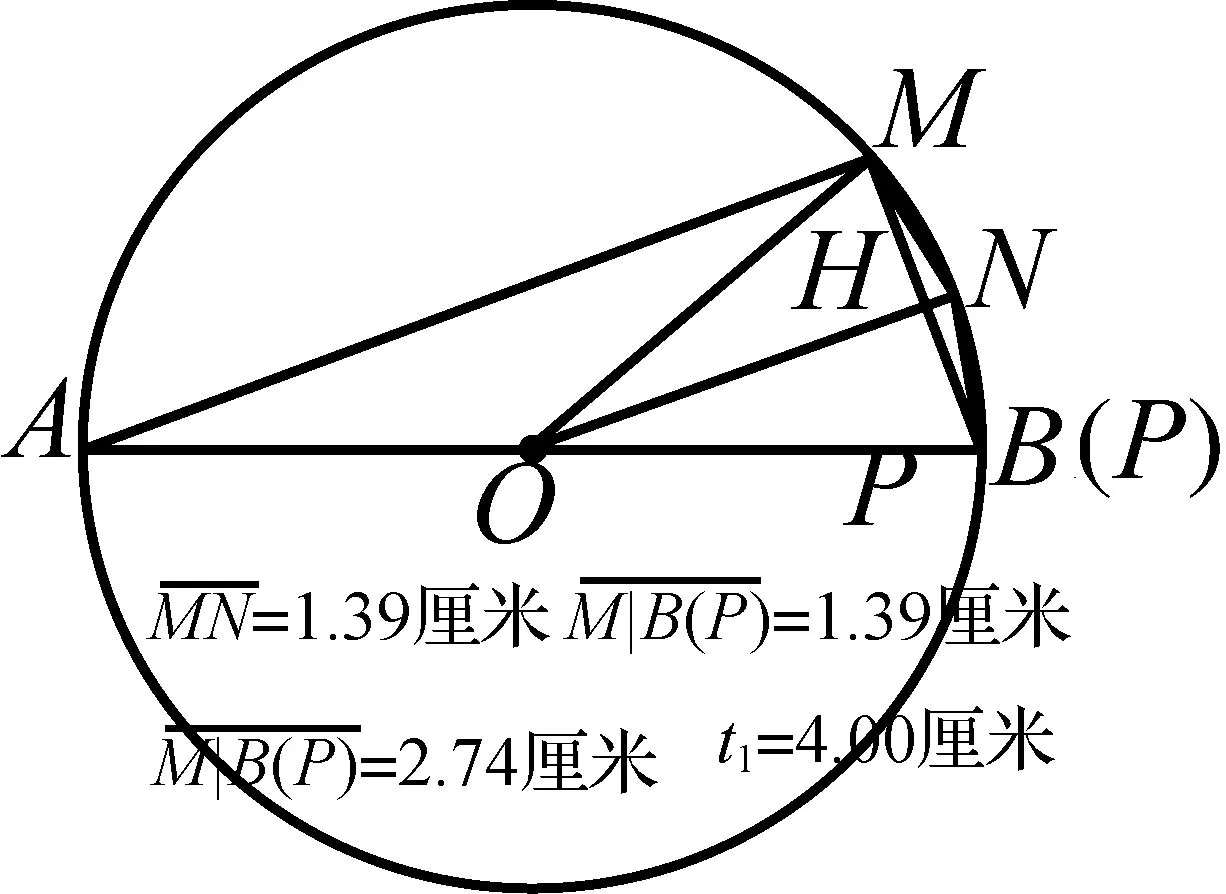
(1)使用几何画板进行了验证：在直径为8cm，∠MAB=20°，N为弧MB中点的条件下，MN=BN=1.39cm,与已知MN=1矛盾.从而确定一定是题目里有隐含的错误.

(2)利用科学计算器，从理论上分析验证：课后针对该题目进行了归谬分析.

(i)分析1：如果AB=8，∠MAB=20°，求MN.

连接MN，OM,ON，作OG垂直于BN,在Rt△BOG中，∠BOG=10°,BG=sin10°×4, 所以BN=MN=sin10°×4×2=0.1736481777×8≈1.39≠1,与已知不符.

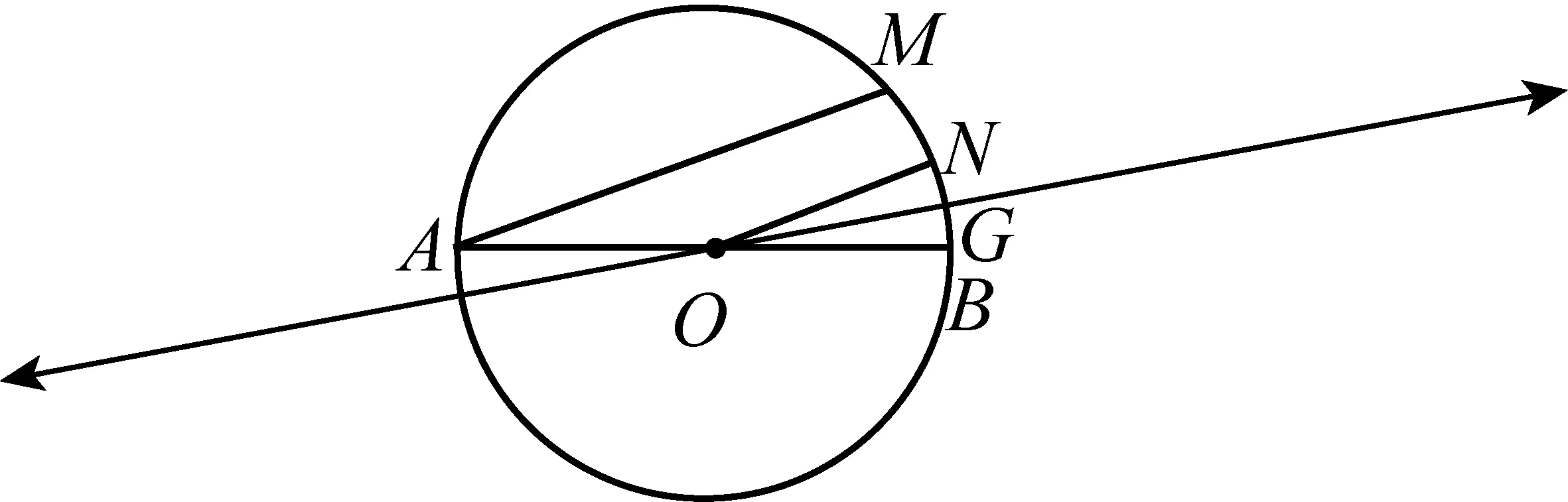
(ii)分析2：如果∠MAB=20°，MN=1，求OB.

连接MN，OM,ON，作OG垂直于BN,在Rt△BOG中，∠BOG=10°,BG=0.5,

所以OB=BG÷sin10°≈2.8793852416≠4,与已知不符.

(iii)分析3：如果AB=8，MN=1,求∠MAB.

连接MN，OM,ON，作OG垂直于BN,sin∠GOB=0.5÷4=0.125，∠GOB≈7.18°,

所以∠MAB=∠MON=2∠GOB=2×7.18°=14.36°≠20°，与已知不符.

数学课堂教学现代教育技术的应用，可以借助计算机，科学计算器，使数学课堂教学通过“计算”去发现结论，笔者利用《几何画板》、科学计算器，以计算的途径，验证了这道中考数学试题的错误.

类比另一道中考试题

如图,AB是⊙O的直径,AB=2,点M在⊙O上,∠MAB=30°,N为弧BM的中点,P是直径AB上的一个动点,则PM+PN的最小值为( )

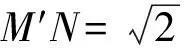
通过类比，发现这道中考数学试题是一个变式，这是数学教学的重要内容.有效的变式，可以增加不少的色彩.但同时必须考虑知识的逻辑顺序，不能为了变式而变式.

结合以上分析，笔者认为这道中考数学在设计方面有误.

课后反思

学生的一个质疑，让我们发现了中考题中的纰漏，学生的这种质疑是不迷信权威，不盲从答案，是难能可贵的独立思考、探究结论的科学研究精神的萌芽，教师要重视和保护每个学生的这种意识.数学教学的意义和生命力应该就在这里吧！