破解题设陷阱,构造函数巧解导数小题
文/梅县东山中学 石 勇
构造函数是解导数问题的基本方法,那么怎样合理的构造函数就是问题的关键,本文详细介绍了导数小题中构造函数的常见方法.
一、与不等式有关的函数构造
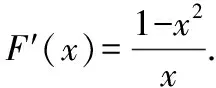
当x∈(1,+∞)时,F′(x)<0,所以F(x)在[1,]+∞)上单调递减,
故当x>1时,F(x) 解题技巧:构造辅助函数,把不等式的证明转化为利用导数研究函数的单调性或求最值,从而证得不等式,而如何根据不等式的结构特征构造一个可导函数是用导数证明不等式的关键. A.有极大值无极小值 B.有极小值无极大值 C.既有极大值又有极小值 D.既无极大值也无极小值 ∴x2f′(x)+2xf(x)=lnx,∴[x2f(x)]′=lnx ∴x2f(x)=xlnx-x+c,将x=e代入可得:e2f(e)=elne-e+c 令g(x)=-xlnx+2x-e则g′(x)=1-lnx, 当x∈(0,e)时,g′(x)>0,当x∈(e,+∞)时,g′(x)<0, 故当x=e时,g(x)取最大值0,故g(x)≤0恒成立,故f′(x)≤0恒成立,故既无极大值也无极小值,故选D. 解题技巧:这类问题在构造函数时,注意逆向思维,构造出的函数的导函数与已知条件相同,或者能够利用已知条件求解. 解题技巧:sinx,cosx因为导函数存在一定的特殊性,所以也是重点考察的范畴,常考的几种形式. F(x)=f(x)sinx,F′(x)=f′(x)sinx+f(x)cosx; F(x)=f(x)cosx,F′(x)=f′(x)cosx-f(x)sinx; 构造函数时注意正弦、余弦的导数公式,尤其注意余弦的导数公式的符号. A.α>βB.α2>β2 C.α<βD.α+β>0 解题技巧:这类题型需要根据题意构造具体的函数关系式,通过具体的关系式去解决不等式和求值问题.二、与等式有关的函数构造

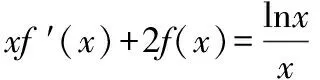
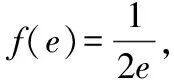
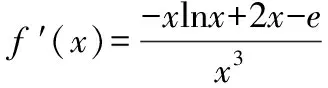
三、与三角函数有关的函数构造
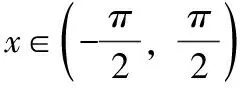


四、具体函数关系式的函数构造