斜支承系统关键件的跌落破损评价

段宁宁，余 立

(1.福建师范大学福清分校 海洋与生化工程学院，福州 350300；2.食品软塑包装技术福建省高校工程研究中心，福州 350300)

上世纪40年代，脆值的定义第一次被Mindlin[1]提出，但难以对其进行精准地确定；60年代，Newton[2]在该定义的基础上提出破损边界；70年代，Newton的理论被应用到ASTM标准中。考虑到产品的破损不仅与冲击加速度最值也与振动疲劳损坏、产品过度变形等有关，Burgess[3]和王振林[4]分别提出疲劳损坏边界、位移损坏边界。王志伟[5-6]、王蕾[7]进一步将上述理论应用到非线性缓冲系统并探讨其在典型波下的冲击响应和破损边界。针对运输过程中作为导致产品破损主要因素之一的跌落冲击，王志伟、胡长鹰、卢富德等研究了非线性系统在典型波作用下的跌落破损边界[8-11]。由于产品受到撞击时会在关键件部位率先发生破损，王军、王志伟、陈安军等提出破损边界曲面，并讨论相关参数对非线性系统关键件的破损评价[12-15]。

根据目前对斜支承系统的研究发现，其具有优良的减振效果[16-17]，孔凡玲、吴晓等研究了斜支承系统在典型波下的冲击特性和位移激励下的强迫振动[18-20]，严敏等[21-23]分别采用变分迭代法、Runge-Kutta法探讨跌落工况下相关参数对系统位移和加速度响应、跌落破损边界的影响。针对考虑关键件的斜支承系统，徐佩霞、陈安军等就系统关键件的振动特性以及典型波作用下的冲击响应与破损评价进行研究[24-30]，而对于系统关键件的跌落破损评价未见有人研究。

本文建立考虑关键件的斜支承系统简化模型，应用四阶Runge-Kutta法求解系统跌落冲击动力学方程，分别以系统参数和跌落冲击初始速度作为2个基本参量，获得系统关键件跌落破损边界曲线；以系统参数、跌落冲击初始速度、支承角或频率比或系统阻尼比作为3个基本参量，获得跌落破损边界曲面，探讨系统支承角、系统频率比、系统阻尼比等对关键件跌落破损边界的影响规律。

1 动力学微分方程及无量纲化

考虑关键件的斜支承双自由度系统可简化为如图1所示：若内装物关键件的质量记为m1、内装物主体的质量记为m2，则m1与m2间的等效刚度系数和阻尼系数记为k1、c1，m2与外包装间的等效刚度系数、阻尼系数和原长记为k2、c2、l0，当斜支承弹簧为l0时的支承角度为ϕ0。

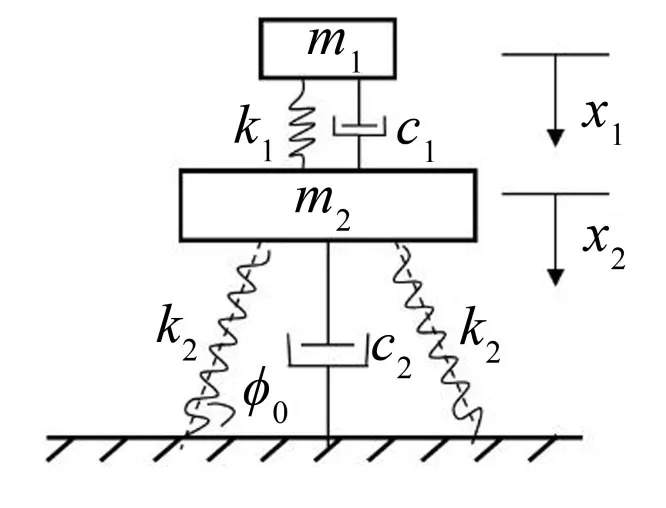
图1 考虑关键件的斜支承双自由度系统

当包装件在H高度自由跌落时，获得系统跌落冲击动力学方程[31]

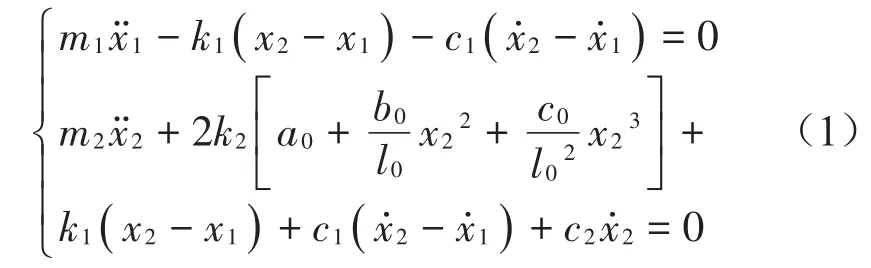
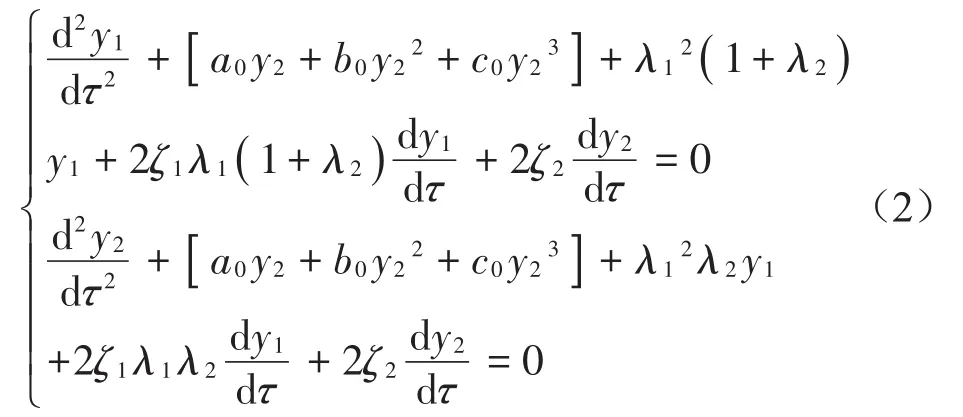
式中 ：频率比λ1=，质量比λ2=，关键件与主体间阻尼比，系统阻尼比。初始条件被无量纲化后变为，，。

由系统无量纲跌落冲击动力学方程（2）知，影响系统关键件跌落破损边界的因素主要有支承角、频率比、系统阻尼比等。

2 系统关键件跌落破损评价

2.1 关键件跌落破损边界曲线

按照脆值定义中的描述，运输过程中为防止内装物发生破损，要求其加速度响应最值不得超过脆值。即为，当系统关键件的脆值为Ac时，内装物加速度响应最值满足。将与式（1）、式（2）相结合，得出

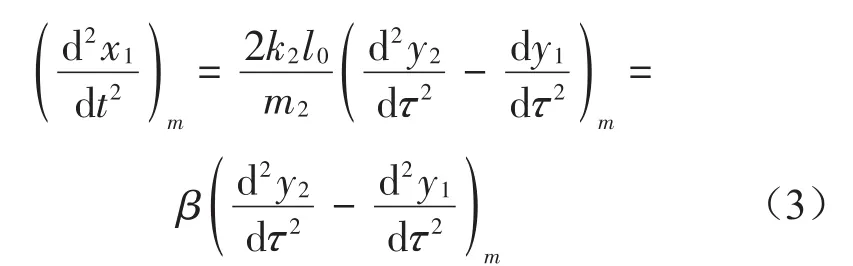
当系统关键件的加速度响应最值为脆值时，则得出

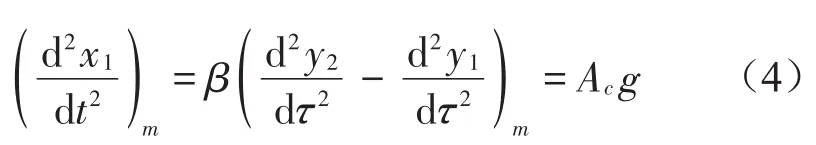
进一步求得

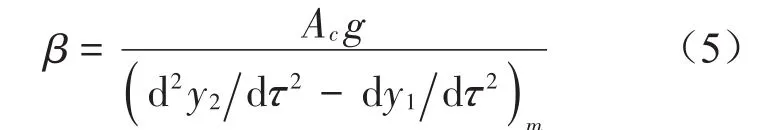
设λ1=10，λ2=0.01，ζ1=0.05，ζ2=0.1，Ac=25，不同ϕ0=600,700,800,900关键件跌落破损边界曲线见图2（a）。由图知，当减小系统支承角时，曲线上移，系统关键件的未损坏区增大。

设ϕ0=700，λ2=0.01，ζ1=0.05，ζ2=0.1，Ac=25，不同λ1=2,3,5,10关键件跌落破损边界曲线见图2（b）。由图知，增加频率比，跌落冲击初始速度V右移，系统参数β上移，未损坏区扩大。

设ϕ0=700，λ1=10，λ2=0.01，ζ1=0.05，Ac=25，不同ζ2=0.01,0.05,0.1,0.2关键件跌落破损边界曲线见图2（c）。由图知，随系统阻尼比的增加，曲线先上移后下移，未损坏区出现先扩大后减小的趋势，因此系统存在最优的阻尼比。

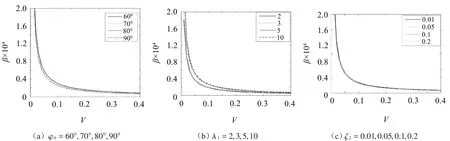
图2 关键件的跌落破损边界曲线

2.2 关键件跌落破损边界曲面

为进一步较为全面地评价支承角、频率比、系统阻尼比等对关键件跌落破损边界的影响，取系统参数β、跌落冲击初始速度V、支承角ϕ0或频率比λ1或系统阻尼比ζ2作为基本参量，获得关键件跌落破损边界曲面，利用Runge-Kutta法求解式（2），探讨系统支承角、频率比、系统阻尼比等对关键件跌落破损边界曲面的影响规律。

设λ2=0.01，ζ1=0.05，ζ2=0.1，Ac=25，当λ1=2,3,5,10时支承角对关键件跌落破损边界曲面的影响见图3。由图知，随支承角下降，曲面上移，系统关键件的未损坏区变大。

设ϕ0=700，λ2=0.01，ζ1=0.05，Ac=25，当ζ2=0.01,0.05,0.1,0.2时频率比对关键件跌落破损边界曲面的影响见图4。由图知，在低频率比范围内，跌落破损边界曲面出现较大波动；在高频率比范围，跌落破损边界曲面趋于平稳，且随频率比增大，曲面上移，未损坏区增大。

设λ1=10，λ2=0.01，ζ1=0.05，Ac=25，当ϕ0=600,700,800,900时系统阻尼比对关键件跌落破损边界曲面的影响见图5。由图知，系统存在最优的阻尼比值；若系统阻尼比低于该值，则未损坏区随阻尼比增大而增大；若系统阻尼比高于该值，则未损坏区随阻尼比增大而减小。

3 结语

基于考虑关键件的斜支承双自由度模型，在跌落动力学方程基础上，应用四阶Runge-Kutta法，获得关键件的跌落破损边界。跌落破损边界结果显示，跌落工况下的影响参数有支承角、频率比、系统阻尼比等，分析结果表明：

（1）支承角的影响。由图2（a）和图3知，减小支承角有利于扩大关键件的未损坏区，缩小损坏区。然而，支承角的减小会导致位移响应最值增大，从而导致产品发生触底。因此，在斜支承包装系统设计时，一般建议选取700≤ϕ0<900。

（2）频率比的影响。由图2（b）和图4知，当频率比小于5时，关键件未损坏区随频率比增大发生显著增加；当频率比大于5时，随频率比增加，破损边界曲线趋于稳定，关键件未损坏区增加不明显；不同于低频率比的较大跌落破损边界曲面波动，高频率比处的跌落破损边界曲面更趋于平稳。因此，合理选择频率比有利于提高斜支承系统的抗跌落冲击性，一般建议λ1>5。

（3）系统阻尼比的影响。由图2（c）和图5知，系统阻尼比存在最优值；低于该值时，未损坏区随阻尼比增大而增大；高于该值时，未损坏区随阻尼比增大而减小。因此，为提高斜支承系统的减振性能，应选择合适的系统阻尼比。

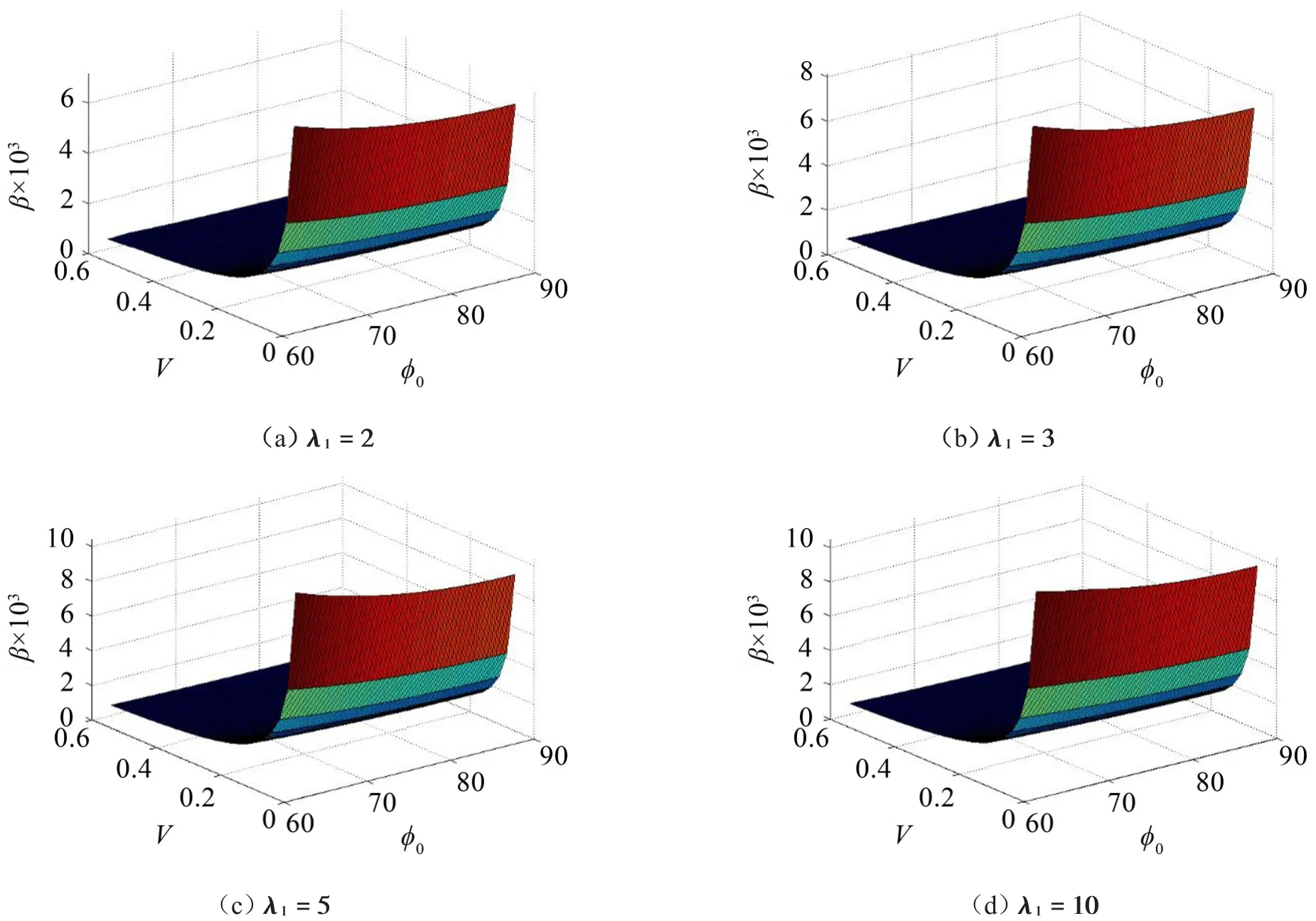
图3 支承角对关键件跌落破损边界曲面的影响

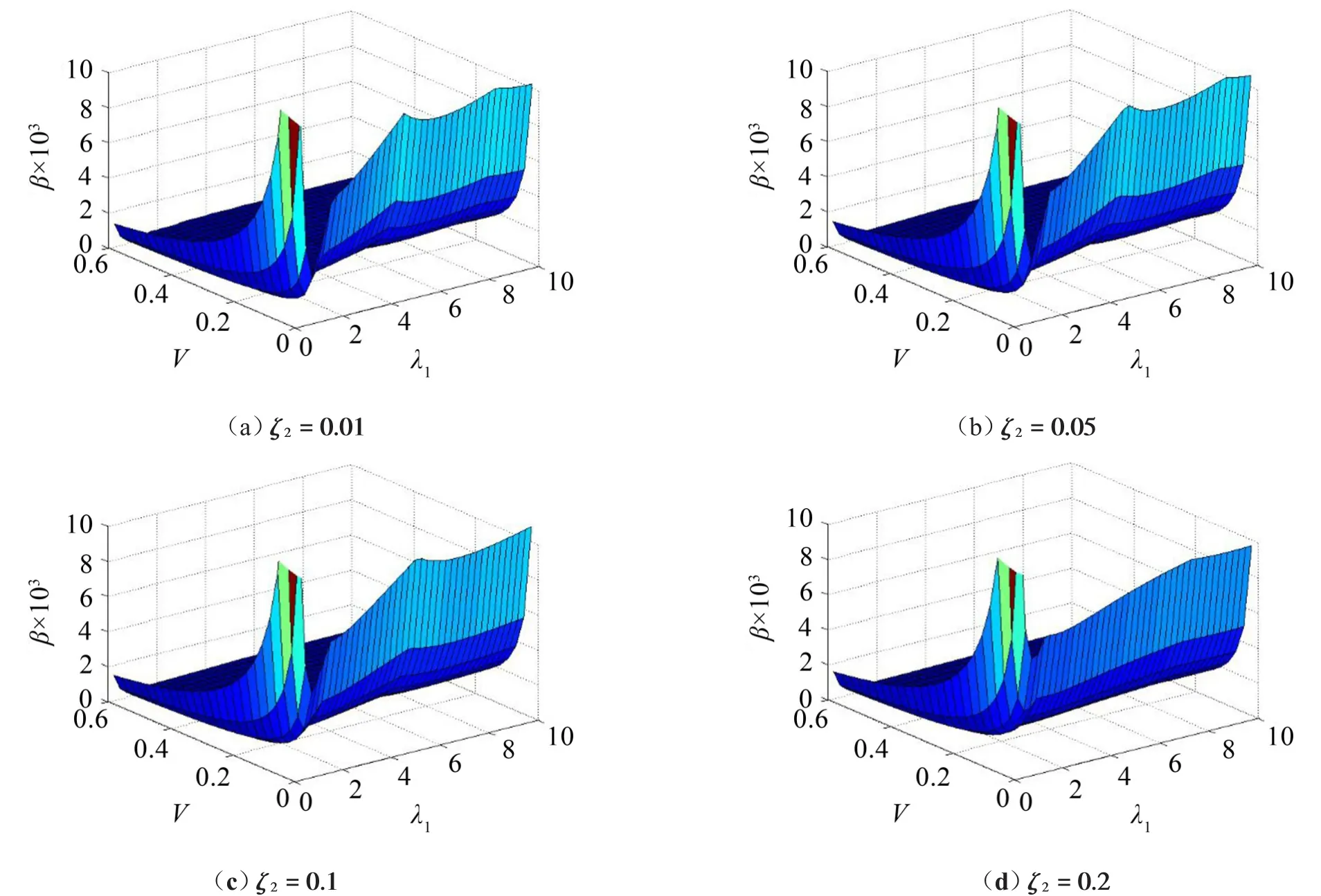
图4 频率比对关键件破损边界曲面的影响

（4）系统参数和跌落冲击初始速度的影响。根据β=2k2l0m2可知，减小内装物主体k2或弹簧原长l0可获得较小的系统参数β；然而，根据V=可知，减小k2或l0可获得较大的跌落冲击初始速度V，从而导致产品发生触底。因此，在缓冲包装系统结构设计过程中，应通过有效控制内装物主体等效刚度系数和弹簧刚度以降低跌落冲击初始速度，从而提高斜支承减振系统的抗跌落冲击性。

图5 系统阻尼比对关键件破损边界曲面的影响