三角、数列强化训练B 卷

■河南省沈丘县第一高级中学 王子瑞

一、选择题

1.已知△ABC的三边长a,b,c成等差数列,且a2+b2+c2=63,则实数b的取值范围是( )。

2.△ABC的内角A,B,C所对的边分别为a,b,c,若a,b,c成等比数列,则( )。

A.角B的最小值为60°

B.角B的最大值为60°

C.角B的最小值为30°

D.角B的最大值为30°

3.在△ABC中,角A,B,C所对的边分别为a,b,c,若sin2A+sin2B=2 sin2C,则cos

C的最小值为( )。

4.在△ABC中,三个内角A,B,C所对的边分别为a,b,c,若sinA,sinB,sinC成等差数列,且,则

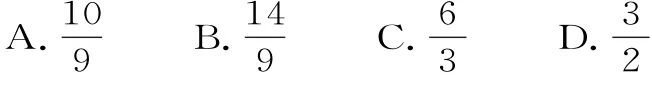
5.在△ABC中,角A,B,C所对的边分别为,且满足A,则的取值范围是( )。

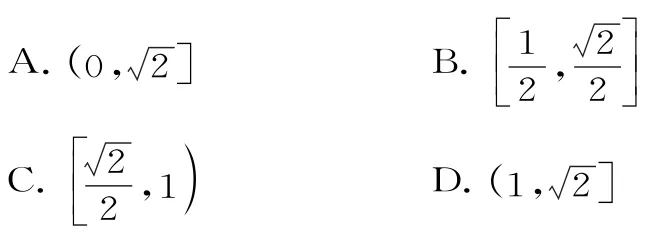
6.在数列{an}中,a1=1,a2018=2018,且对任意n∈N*都有2an+1≥an+an+2,则下列结论正确的是( )。

A.对常数M,一定存在正整数N0,当n＞N0时,都有an≥M

B.对常数M,一定存在正整数N0,当n＞N0时,都有an≤M

C.存在正整数N0,当n＞N0时,都有an≥n

D.存在正整数N0,当n＞N0时,都有an≤n

7.已知函数f(x)=sin(x-3)+x-1,数列{an}是公差不为0的等差数列,若f(a1)+f(a2)+f(a3)+…+f(a7)=14,则a1+a2+a3+…+a7=( )。

A.0 B.7 C.14 D.21

8.已知函数y=a+sin

b x(b＞0且b≠1)的图像如图1所示,则函数y=a|x|-b的图像可能是图2中的( )。

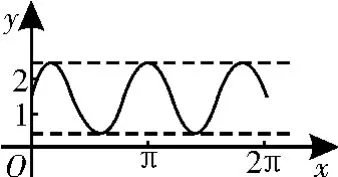
图1

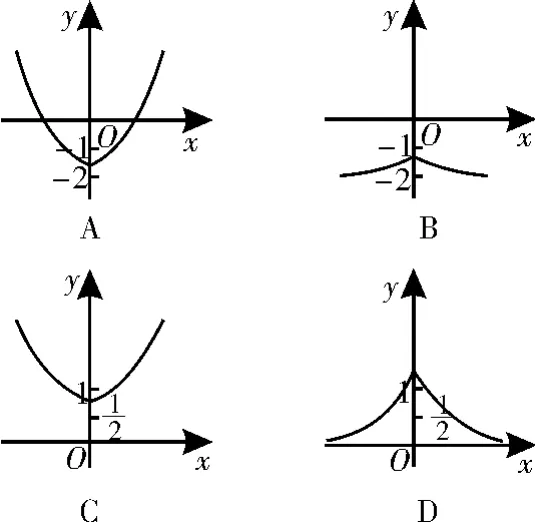
图2

9.如果△A1B1C1和△A2B2C2满足则称△A1B1C1

111

10.已知数列{an}满足an+1=an+an-1(n∈N*,n≥2),则和△A2B2C2是一对“友好三角形”。那么下列结论正确的是( )。

A.△A1B1C1和△A2B2C2都是锐角三角形

B.△A1B1C1和△A2B2C2都是钝角三角形

C.△A1B1C1是钝角三角形,△A2B2C2是锐角三角形

D.△A1B1C1是锐角三角形,△A2B2C2是钝角三角形的整数部分为( )。

A.0 B.1 C.2 D.3

11.方程在上有两个不相等的实根,则实数a的取值范围是( )。

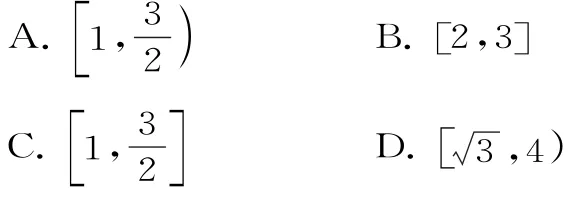
12.如图3,在半径为1的扇形AOB中(O为原点)点P(x,y)是上任意一点,则x y+x+y的最大值为( )。

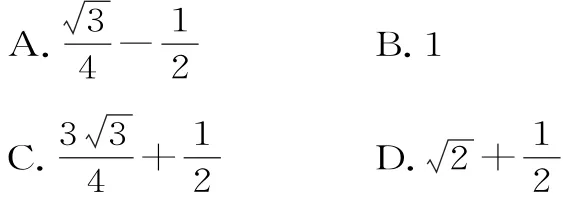
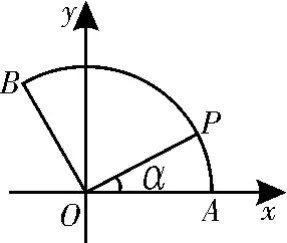
图3

二、填空题

13.已知某台风中心位于海港城市A东偏北α的150k m外,以每小时v

k m的速度向正西方向快速移动,2.5h后到达距海港城市A西偏北β的200k m处,若4 cosα=3 cos

β,则风速

14.已知,则cos2α的取值范围是____。

15.在△ABC中,角A是B,C的等差中项,∠BAC的平分线交BC于点D,若AB=4,且,则AD的长为____。

16.已知函数在区间和上均为单调递减,记M,则M的取值范围是____。

三、解答题

17.(1)设,其中,求的值。

18.设△ABC的内角A,B,C所对的边分别为a,b,c,a=bt a nA,且B为钝角。

19.已知Sn为数列{an}的前n项和,且满足Sn-2an=n-4。

(1)证明{Sn-n+2}为等比数列;

(2)设数列{Sn}的前n项和为Tn,求Tn。

20.已知数列{an}各项都是正数,且

(1)求数列{an}的通项公式。

(3)是否存在整数m,使得成立?若存在,求出m的值;若不存在,请说明理由。

21.如图4,在平面直角坐标系中,锐角α和钝角β的终边分别与单位圆交于A,B两点。

图4

(1)如果点A,B的纵坐标分别为求cos(α+β);

(2)若∠AOB=90°,M为x轴上异于O的点,且MA⊥MB,求点M横坐标的取值范围。

22.已知数列{an}满足：a1=1,an+1·(an+2n)=an·2n+1(n∈N*)。

(2)若数列{bn}满足且数列{bn}的前n项和为Sn。若对任意的n∈N*,t∈[1,3],不等式(a＜0)恒成立,求实数a的取值范围。