基于博弈论的医药供应链合作问题研究

（南京航空航天大学 经济与管理学院，江苏 南京 210000）

1 引言

自2009年新医改颁布和实施以来，医药体制方面不断出台新的政策方案，试图降低药品价格，缓解人民群众“看病难，看病贵”的问题，但均未取得明显的效果。药品价格虚高在中国药品市场中一直是一个比较严重的问题，是流通体制改革政策层面的问题。与发达国家的药品流通相比较，我国医药流通领域的资源分配不均，基础设施建设不到位；物流和供应链管理技术发展滞后，同时缺少信息化技术的应用，导致医药物流不够专业化，严重滞缓了第三方物流的发展[1-2]；医药流通领域的产业集中度偏低，产业格局呈现“小、散、乱、多”的局面[3-4]。此外，医药供应链企业之间缺乏合作意识，只关注自身利益，很少考虑供应链中其他企业的利益及最终消费者的利益[5]。医药供应链中企业不合作，导致整个医药供应链成本高且效率低，无法实现经济最优化。本文正是在我国医药行业这样的背景下，基于博弈论，对医药供应链企业合作与不合作之间的差异进行研究。

2 博弈模型构建

本文博弈分析构建的模型是由医药生产企业、医药流通企业、医药零售商以及最终的患者组成的三级供应链博弈模型，如图1所示。医药生产企业将生产出的药品提供给医药流通企业，医药流通企业再将其通过层层代理商分销给各医疗机构及零售药店，最终患者到医院或零售药店购买药品。

图1 医药供应链结构模型图

2.1 模型假设

为了简化本文的博弈分析，本文做了以下假设：

（1）只针对单一药品的医药供应链；

（2）各节点企业对药品的定价在销售期间保持不变；

（3）不考虑未售完药品的残值；

（4）不考虑药品在订购、运输及销售过程中的丢失、损毁等意外情况；

（5）药品属于非垄断性药品，市场化程度较高，属于完全竞争市场。

2.2 符号说明

为了方便问题的阐述与分析，对于建立的医药供应链结构模型，本文规定了以下符号：

D：市场基础需求量；

c1：医药生产企业生产药品的成本；

p1：医药生产企业提供给医药流通企业的药品价格；

c2：医药流通企业的流通成本；

S：医药流通企业的服务水平；

p2：医药流通企业分销给医药零售商的药品价格；

c3：医药零售商的运营成本；

p3：医院或零售药店最终销售给患者的药品价格；

Q：药品总供应量，即市场需求量；

π1：医药生产企业的利润；

π2：医药流通企业的利润；

π3：医药零售商的利润；

πt：医药供应链总利润，即医药生产企业、流通企业及零售商的利润之和。

上文假设所研究的药品属于完全竞争市场，根据完全竞争市场的一般规律，市场需求量与价格呈反相关，与服务水平呈正相关，即药品的最终销售价格越低，服务水平越高，市场需求量就越大；药品的最终销售价格越高，服务水平越低，市场需求量就越小。因此，药品市场需求量Q与药品最终的销售价格p3以及医药物流企业的服务水平S的关系式如下：

式中：a为价格弹性系数，b为服务弹性系数，a,b＞0,且均为常数。

由式（1）可反推出药品的最终零售价格为：

企业服务成本是服务水平递增的严格凸函数,即随着服务水平的提高，服务成本也会相应地升高，它们之间具有二次形式的关系[6-8]。所以，医药流通企业的流通成本c2与其服务水平S具有如下关系：

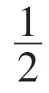
基于上文假设的本文所研究的药品为非垄断性药品，属于完全竞争市场，所以医药生产企业、医药流通企业及医药零售商的利润可分别用如下公式表示：

医药生产企业的利润：

医药流通企业的利润：

医院或零售药房，即医药零售商的利润：

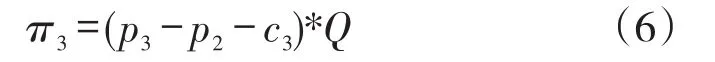
因此，医药供应链的总利润：

将式（4）—（6）带入式（7）得：

3 博弈分析

3.1 非合作博弈分析

基于上一节建立的包括医药生产企业、医药流通企业和医药零售商的三级医药供应链博弈模型，本节分析各供应链成员企业之间不合作，即独立决策的情况。此节针对这种在医药市场普遍存在的情况，进行完全信息动态Stackelberg博弈分析。

在这种市场情况下，医药生产企业在整条供应链中处于比较强势的地位，首先会做出自己的决策：综合考虑医药生产成本、市场形势等因素，给出药品的出厂价格p1，并提出满足自身利益最大化所需要的医药流通企业提供的药品服务水平S。然后，医药流通企业依据自己的流通成本c2，医药生产企业提供药品的价格p1及所需药品服务水平S，同时综合考虑市场情况，确定药品分销给零售商的价格p2，以满足自身利润的最大化。最后，医药零售商会根据医药流通企业提供的价格p2，并考虑自身的运营成本c3，确定药品的零售价p3及采购数量Q，来满足市场需求。此博弈的解称为Stackelberg均衡。

在求解这个博弈模型时，采用逆向归纳法来求解其均衡值，即从动态Stackelberg博弈的最后一步向第一步反向推导。

首先，将式（2）代入式（6）中，求得医药零售商的利润函数为：

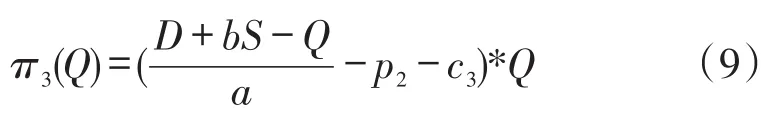
由于π3''(Q)＜0，所以医药零售商的利润π3是关于药品订购量Q的凹函数，即当π3'(Q)=0时，医药零售商的利润π3最大。求解得到最优订购量Q为：

再将式（10）的结果代入式（2），得到医药零售商的销售价格p3为：

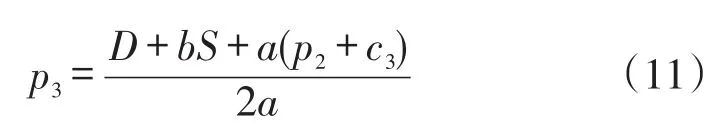
然后将式（10）代入式（5）中，得到医药流通企业的利润函数为：

由于π2''(p2)＜0，所以医药流通企业的利润π2是关于医药流通企业分销给零售商的药品价格p2的凹函数，当π2'(p2)=0时，医药流通企业的利润π2取最大值。此时求得医药流通企业的分销价格p2为：

再将式（13）求得的p2及式（10）代入到式（4），能够得到医药生产企业的利润函数为：

由于π1''(p1)＜0,π1''(S)＜0，因此医药生产企业的利润π1是关于医药生产企业提供给医药流通企业的药品价格p1及药品服务水平S的凹函数，即当π1'(p1)=0,π1'(S)=0时，医药生产企业的利润π1取到最大值。此时求得：

将式（15）、（16）依次回代入式（13）、（11）以及式（10），可以求解得到医药流通企业的分销价格p2、零售商的销售价格p3以及订购量Q的最优值分别为：

最后，将以上计算结果分别代入式（4）—（7），可以求得医药生产企业、流通企业、零售商的利润，以及医药供应链的总利润分别为：

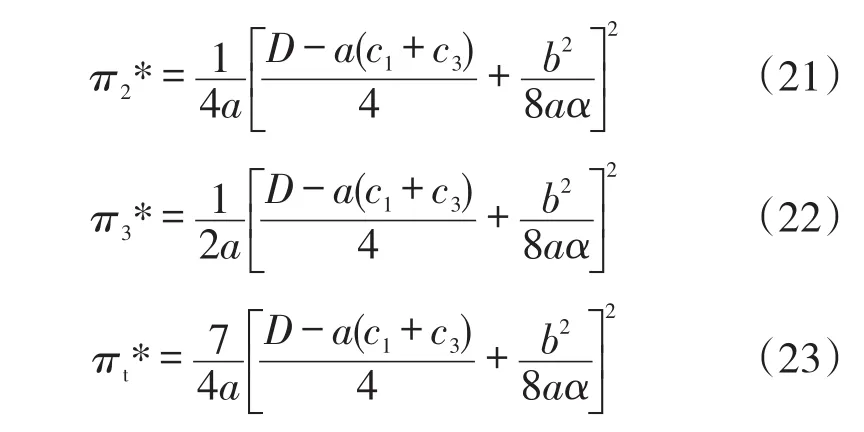
3.2 合作博弈分析

上一小节分析的是医药供应链中各企业彼此间不合作的模型，医药生产企业、流通企业及零售商分别从自身利润最大化的角度考虑，独自制定价格。这种非合作博弈在实际医药供应链的运作过程中会导致效率低下，无法达到整体供应链的最优状态。因此，本节从医药供应链中各企业互相合作，即合作决策的角度出发，对其进行合作博弈分析。

在合作博弈的过程中，医药供应链中的所有成员企业都基于整个供应链实现利润最大化的目标做出决策。因此，在博弈分析中，以整条供应链作为决策分析单元，不用考虑各成员企业各自的成本及定价，只需考虑医药供应链的整体服务水平S以及药品供应量Q。

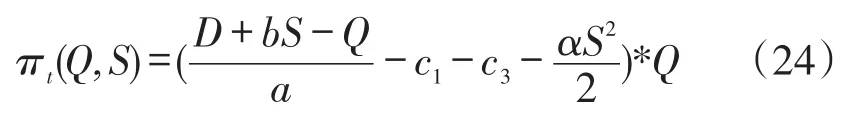
将式（25）、（26）代入式（2），可算得此时医院或零售药店最终销售给患者的药品价格为：

此时，医药供应链的总利润取得最大值，为：

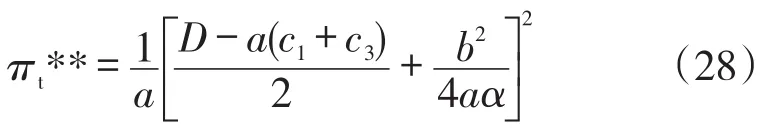
4 不同博弈下的结果比较

将医药供应链成员企业非合作博弈及合作博弈两种情况下的结果进行对比，主要从供应链的服务水平、药品零售价格、订购量及供应链的总利润四个方面进行对比，具体见表1。

表1 不同决策下的结果比较

从表1可以得到以下结论：

结论1：非合作博弈时的医药供应链服务水平S与合作博弈时相同；

结论2：合作博弈时的药品零售价格p3比非合作博弈时的零售价格低；

结论3：合作博弈时的药品订购量Q是非合作博弈时订购量的4倍；

结论4：合作博弈时的医药供应链总利润πt是非合作博弈时供应链总利润的2倍多。

5 结论

本文基于博弈分析发现，对于整个医药供应链系统而言，合作博弈下供应链的各项绩效指标都会明显优于非合作博弈。在同等服务水平下，合作博弈在很大程度上提高了药品的供应量，降低了药品的最终销售价格，并且提高了整个医药供应链的利润。因此，整个医药供应链的协调是尤为重要的。只有统筹医药供应链各成员企业间的目标冲突，建立密切的合作关系，整合上下游企业的信息和资源，并实现信息和资源的共享，促进各成员企业彼此间的合作，才能使整个医药供应链系统向着最优状态靠近。