基于车公里成本的多车型车辆规划方法

剑，张俊丽，官静萍

（1.湖南科技大学 资源环境与安全工程学院，湖南 湘潭 411201；2.湖南科技大学 知识处理与网络化制造湖南省实验室，湖南 湘潭 411201）

1 引言

作为一类经典的NP-hard问题，车辆路径问题（VRP）一直是现代物流领域的研究热点。随着研究的不断深入，VRP问题更趋向于具体化和实用性，譬如增加仓库约束、车型装载量约束、装卸顺序约束、时间窗约束等。目前VRP的方法主要分为两类：精确算法和启发式算法。启发式算法的求解精度虽不如精确算法那么高，但是因其时间效率表现更为明显而受到青睐，或者将两种算法相结合改进求解质量。

实际上，车辆路径问题主要包括车辆规划和路径规划。车辆规划问题和路径规划问题相互制约，相关学者一般分为两种，一是先车辆规划后路径规划，二是车辆规划和路径规划同时进行。从先车辆规划后路径规划的角度而言，当前的研究主要集中在单车型VRP问题上，并对此提出一系列的启发式算法及改进方式，计算步骤一般为依据最高装载率原则，得到货物配送所需的最少车辆数，如Barrie M[1-6]等运用遗传算法求解单仓库单车型VRP问题；梁承姬[7-9]等利用蚁群算法并加以改进优化求解单车型VRP问题；刘春苗等[10]运用禁忌搜索算法求解带时间窗的单车型VRP问题；马华伟等[11]运用禁忌搜索算法求解带时间窗的单车型VRP问题；胡云清等[12-13]采用改进萤火虫算法求解单车型VRP问题。从车辆规划和路径规划同时进行求解的角度而言，Petrica C[14]通过结合局部-全局算法对遗传算法进行改进，车辆问题和路径问题同时考虑求解单车型VRP问题。在单车型VRP问题中，所需车辆数可以依据总货物量进行约束，以最高装载率优先得到高质量解。

而在现实物流配送中，为了满足不同客户需求，往往是多种车型进行同时配送。在多车型VRP问题中，因为车型装载的限制不同，其车型的可用组合数增加，VRP问题的求解更为多样。针对多车型VRP问题的相关研究较少，卢冰原等[15]基于混合粒子群算法求解多车型调度问题；熊浩等[16]以最小油耗为目标利用改进遗传算法求解多车型动态车辆调度问题；Wenbin Zhu[17]认为在多车型VRP问题中，难点在于车型组合的不确定性。相关学者往往将全部可能的组合进行考虑，虽然可以提高全局的最优解，但也同时增加了问题的复杂性。

在单车型VRP问题的求解中，需要在VRP的路径规划之前，先进行货物量或者总流量与当前车型的装载率要求，选出本次派送需要的最少车辆数，然后在此基础上，运用各自的搜索策略逐步求解，但也暴露了一些问题。VRP问题求解不单单是指车型装载的约束，与途中的各个运输路径均有关系，整个路径规划应该是总体最优的结果；其二是对于多种车型而言，这种车型的简单约束并不能反映出问题，在路径规划中，大小不等的车型相互配合，路径的不同也会对车型组合产生影响。所以在多车型VRP问题的求解中，目前的文献研究多是通过将路径与车型结合动态规划最终结果，运用车型组合与路径规划动态规划，最优近似解的质量相较于单车型VRP问题更为合理，更加符合实际需求。不足之处在于动态规划过程中，车型组合数量的不确定增加了搜索的更多可能性，增加了求解的时间复杂度。

本文的出发点在于依据实际物流配送中的多车型问题，借鉴相关学者的经验，以行政区域作为分区标准，加以车公里成本约束条件和距离估算模型，基于分枝定界思想构造多车辆规划整数模型，为路径规划前的车辆调度提供更为精确的理论支撑和数据对比，从而得到VRP问题的更高质量解。

2 货物配送距离分析

2.1 距离成本

在当前的各种VRP求解中，关键在于如何在装完所有货物的前提下，使得货物的总配送成本最低。假设在实际配送中，如果对较远的区域配送，尽量一次性用大车型装载区域较远的货物，把不必要的途中配送成本降低，而非利用多辆小车型进行多次往返配送，显然前者的成本会更低。

货物配送是一个非常复杂的过程，区域大小和客户点分布程度都影响着运输方案的复杂程度。实际配送中一般选用分区配送的方法提高配送的效率，分区配送就是把大型区域划分成较小区域来配送货物，在研究过程中，配送距离划分为两部分，即仓库点至配送区域外围的车辆外部单向行驶距离L1和配送区域内部车辆行驶总距离L2，在图1中，仓库点A为配送中心，配送区域R，区域内部包含客户点和单车辆配送路线。在一次货物配送过程中，配送总成本Costall包括区域外部配送总成本CostL1和区域内部配送总成本CostL2：

在上述公式中，总货物量为W，仓库有n种车型{0,1,2,...,n},其中wi表示车型i的额定装载量，Ci表示车型i的车公里成本，xi表示车型i在本次配送中所需的车辆数，q为本次配送的平均装载率，一般取值为0.85-0.90。式（1）表示总配送成本包括区域外部配送总成本CostL1和区域内部配送总成本CostL2；式（2）表示按照车型i所需车辆数xi在外部的往返配送成本为xi*2L1*Ci，可得到区域外部配送总成本CostL1；式（3）表示xiTi为本次配送过程中车型i在区域内部的行驶距离，车型i在区域内部的配送成本即为xiTiCi，可得到区域内部配送总成本CostL2；式（4）表示由配送区域内部行驶的总距离依据每辆车的平均装载量占总货物量的比重来计算在本次配送中每辆车在区域内部的行驶距离Ti。

图1 区域配送图

2.2 分区配送距离估算

在分区配送过程中，区域外部配送总成本CostL1由已知的车公里成本数据和L1可计算得到，主要在于计算区域内部配送总成本CostL2，由公式（3）可知，CostL2可依据Ti得到，而车型在区域内部的行驶距离Ti是动态的，而Ti依赖于L2。在按照行政区域规划的分区标准，区域分布离散度表示区域内各客户点的地理分布程度。对于每一个待配送区域，区域分布离散度各不相同，待配送区域内部的客户在地理位置上随机分布，客户点的各货物需求量也不同，L2也随之不确定。即使同样的客户数和配载货物量，由于区域分布离散度的不同，区域内部的配送距离L2也会有所变化。

在L2的计算过程中，Bahar Cavdara[18]提出了一个基于随机分布点的TSP距离估算模型：

式（5）中L2即本配送区域内部估算车辆行驶总距离，n为本次待配送区域内客户点数量，A为配送区域面积，首先从百度API接口获取客户点的经纬度坐标，可以计算出配送区域中心点C的坐标，为各客户点到区域中心点C的平均距离，距离的衡量标准采用百度距离，符合实际需求；stdevx,stdevy为客户点经纬度坐标的标准差，衡量客户点的总体分散程度，整体区域客户越分散，值越大；cstdevx,cstdevy为各客户点与中心点的绝对距离的标准差，表示各客户距离区域中心的分布程度。

由式（5）计算出区域内部配送估算总距离L2，此时得到客户点之间的平均距离D为(L2/n)，区域分布离散度R为(stdevx2+stdevy2)/n。

由表1得到平均距离D与区域分布离散度R之间的线性回归方程：

图2为部分区域的区域分布离散度R与平均距离D及其线性回归方程趋势线。

表1 区域分布离散度R与平均距离D

图2 平均距离与区域分布离散度的线性方程

3 车公里成本车辆规划模型

3.1 模型确定

本文的问题描述：在实际派车过程中，以某物流中心作为货物配送中心，配送中心已选取好待配载车型及其数量进行集中配送。在项目的实施过程中，配送步骤为：统计当天的波次订单，然后依据货物总量和已有车型选出装载组合，然后进行路径规划。

模型中所需变量描述：假设某物流仓库点有W体积待配载货物，有n种车型可供选择：{m1,m2,...,mn}，各车型数量上限：{n1,n2,...,nn}辆，各车型额定装载量：{w1,w2,...,wn}体积，各车型的每公里油耗：{C1,C2,...,Cn}，各车型的最高装载率：{q1,q2,...,qn}，假设本次配送各车型需要{x1,x2,...,xn}辆，车辆外部单向行驶距离为L1，车辆内部行驶总距离为L2。

目标函数：

约束条件：

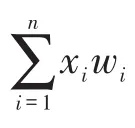
3.2 算法步骤

本文模型基于分枝定界法[19-20]的思想进行构建，分枝定界法作为一种在问题的解空间树上搜索问题界的算法，在满足约束条件的解中找出使目标函数值达到极大或极小的解，即最优解。其策略是，在扩展结点处，先生成其所有的儿子结点，以加速搜索进程，在每一活结点处，计算一个函数值，并根据这些已经计算出的函数值，从当前活结点表中选择一个最有利的结点作为扩展结点，使搜索向着解空间树上最优解的分支推进，以便尽快找出一个最优解。

本文的整数规划模型应用分支定界思想的计算步骤如下：

定义最大油耗成本为Costmax，最小油耗成本Costmin；

（1）先将上述模型中目标函数问题P转换为相应的线性规划问题P'求解，若P'无解则无解；若P'有解，且xi均满足整数条件，则{x1',x2',...,xn'}即为最优解，最优运输成本为Cost'；若P'有解，但不符合整数条件，Costmax即Cost'。

（2）分枝：寻找此时解空间的非整数车型解，例如车型解的第一个非整数为x1'，构造两个约束条件x1≤floor(x1')和x1≥floor(x1'+1)；将这两个条件重新加入到约束条件模型中，进行计算。

（3）定界：以每个后继问题为一分枝标明求解的结果，在其它问题解的结果中找出最大配送成本作为新的Costmax，从已符合整数车型解的各分枝中找出最大配送成本作为Costmin。

（4）比较与剪枝：各分枝的最优车型解的运输油耗成本若小于最大配送成本Costmin，则剪掉这枝，以后不再考率；若大于最小配送成本，且不符合整数条件，则重复（1）步骤，直到Costmax-Costmin在误差范围内，保存此时的车型解，即为最优车型组合{x1,x2,...,xn}，最优配送成本为Costmin。

4 实例数据对比分析

实际案例描述，仓库中心分布于湖南省湘潭市岳塘区内，分区配送区域见表2，包括近距离区域（湘潭市雨湖区）、中距离区域（娄底市娄星区）以及远距离区域（常德市鼎城区），选定每个区域的一个波次订单开始配送。车型为仓库中心已有可用车辆，车型按照体积大小排序为{a,b,c,d,e,f,g,h,i,j}，车公里成本数据见表3，L1因为中心仓库点和各配送区域虚拟仓库点均为固定而固定，由于波次订单的不同，依据式（5）动态计算L2，下面各实例A1-YH-14979（实例编号-区域编号-货物总量）将考虑距离成本的分支定界算法与只考虑装载率不考虑距离成本的一般精确算法进行最终配送成本的对比，见表4。实验数据对比包括同一区域不同货物量的配送成本比较和不同区域间的配送成本对比，在当前实例中车型组合的构成对比如图3所示，同一实例左侧为本文模型计算得到的车型组合构成，右边为只考虑装载率的一般精确算法结果。

表2 仓库点、各分区坐标和L1

表3 车型体积及车公里成本

从实验结果可以看出：（1）在表3中，对于不同区域，在添加车公里成本约束条件之后，基于车公里成本的车辆规划模型计算的配送总成本均得到不同程度的优化，尤其在较远区域（鼎城区），成本优化比高达80%；（2）对于同一区域，选用不同的初始车型组合，较大车型组合的配送成本更低；（3）图3中，在同一实例数据的对比中，左侧基于车公里成本模型的车型组合结果相较于右侧只基于装载率模型的车型组合结果，大车型选择占比更高，配送总成本更优。

表4 配送成本对比

图3 车型组合对比

5 结束语

在物流配送中，装载率最优并非总成本最优，车公里成本约束使得总成本最低更切合实际。单考虑装载率约束的组合装载成本并非最优，这表现在当一些小车型可以满足最高装载率的同时，组合装载所用到的车型数量也会有所增长，而车型总数量的增加在较远距离运输中，导致物流运输总成本也随之大幅提高。在远距离运输选用大车型时，一辆大车的运输成本往往低于两辆甚至多辆小车型组合运输的成本。由实验数据分析，加入车公里成本的考量，可以使得在路径规划前的车辆装载调度表现更为合理。在进行启发式算法的路径规划前，合理的进行车辆控制尤为必要。