压电材料矩形板的热振动分析

李林利， 薛春霞

(中北大学 理学院， 山西 太原 030051)

0 引 言

压电材料的发展极为迅速， 广泛应用于压电滤波器、 微位移器、 驱动器和传感器等电子器件中， 在卫星广播、 电子设备、 生物以及航空航天等高新技术领域都有着重要的地位. 而结构在热荷载下的动力响应问题是目前工程结构热分析的主要研究内容之一. 结构热动力响应主要表现为热振动， 持续的热振动又会引发结构的疲劳和破坏， 是结构受热失效的主要形式. 故分析压电材料在温度场下的动力响应具有很实际的工程意义. 九十年代初期以来， Bao Y等[1]研究了电场、 热场共同激励下的压电层合梁的静力学问题和压电驱动器通过控制电压施加的非线性静态挠度和固有频率的主动控制效果. 田振国等[2]讨论了载流板的温度、 应力、 位移与外加电磁场、 温度场以及机械载荷的关系. 王书鹏[3]在传统弹性梁振动理论基础上， 通过变换振动系统的位移表达,推导出了弹性支承梁在均布矩形脉冲和三角形脉冲两类冲击荷载下的耦合振动解析解. 李世荣等[4]对压电层功能梯度梁在横向非均匀升温和均匀驱动电压作用下的几何非线性大变形以及大变形构型附近的自由振动进行了定量分析， 分析了热荷载和材料梯度性质对变形和振动特性的影响. 苏厚德等[5]研究了上下表面粘贴压电层的功能梯度材料梁在升温及电场作用下的振动以及过屈曲行为. 王涛等[6]用ANSYS有限元计算方法对压电智能结构机电耦合效应下的动力学性质进行了分析. Lee H J等[7]基于分层有限元理论研究了电、 热共同作用下功能梯度压电双晶梁的位移和应力问题， 并分析了电和热负荷对双芯片驱动器的挠度和应力的影响. 叶文强等[8]对压电振子受纵向冲击时的波动问题进行了研究. Kapuria S等[9]对对称叠层简支钢梁在电热荷载作用下的屈曲问题进行了分析. 薛春霞等[10]利用Karman关于板的大挠度理论导出了在横向磁场和横向载荷共同作用下薄板的非线性运动方程. 由于压电结构的材料特性具有广阔的应用前景， 而人们对它的应用研究时间并不长， 要充分实现其功能， 有许多方面的问题需要研究和解决.

鉴于高温环境对压电材料结构的振动行为有很大的影响， 但目前很少有文献涉及压电材料矩形板的热振动分析， 本文在现有文献的研究基础上， 对于压电材料二维板结构， 通过弹性力学基本理论、 Bubnov-Galerkin原理、 多尺度法等推导出了外激励和恒定温度场作用下的非线性振动方程和协调方程， 求得压电材料矩形板主共振时的幅频响应方程和相频响应方程. 用ANSYS软件进行算例分析， 讨论了不同的恒定温度场对矩形板的振动频率和振幅的影响， 并分析了振动系统最大应力变化规律.

1 压电材料矩形板的基本方程

以压电材料矩形薄板为研究对象. 以薄板的中面为xoy面， 它的法线为z轴， 如图 1 所示. 假设板长为a， 宽为b， 高为h， 薄板上侧受外激励为均布力q=q0cosωt.

图 1 压电材料矩形板结构Fig.1 Rectangular plate structure of piezoelectric material

对于横观各向同性压电材料的矩形薄板， 在考虑温度效应时的压电方程[11]为

(1)

式中：t31=Eα/(1-υ)为热-机械耦合常数，E和υ分别为杨氏模量和泊松比，α为线性膨胀系数；c11,c12,c21,c22,c66为压电材料的刚度；e31为压电系数；ε3为介电系数；m3为热-压电耦合常数；E3为电场；T为温度增量；σx,σy和τxy分别为x方向和y方向的正应力和切应力；DE为电位移；S为熵；α0=C/T0，C为比热，T0为初始温度. 由Von Karman板大挠度理论[12]， 位移与应变的关系为

(2)

薄膜内力

(3)

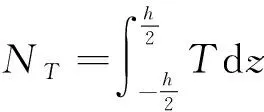
弯曲内力

(4)

板的运动方程[13]

(5)

式中：Qx,Qy分别为垂直于x轴及垂直于y轴的截面上单位宽度的横向剪力. 由于c11=c22， 注意到c11=c12+2c66， 将Mx,My,Mxy,Nx,Ny,Nxy代入平衡方程， 得到压电材料矩形板的横向热振动方程如下

D4w=hL(φ,w)-e312ME-t312MT-

(6)

引入应力函数， 有

(7)

应变协调方程变型为

(8)

2 非线性热振动方程近似解

对于四周简支的压电材料矩形板， 可将横向位移w设为

(9)

式中：X(t)为板中心的无量纲挠度的最大值.

由方程(6)， (8)和(9)， 利用Bubnov-Galerkin原理， 并引入瑞利阻尼得到动力学方程为

(10)

式中：

Z=αm+αkkl，

αm,αk为阻尼系数.

进行无量纲化， 令

则系统的无量纲方程变为

(11)

式中：

满足初始条件

(12)

用多尺度法求解无量纲方程

(13)

便得到主共振时的幅频响应方程和相频响应方程分别为

(14)

(15)

3 算例分析

3.1 模态分析

钛酸钡材料的参数值如表 1 所示.

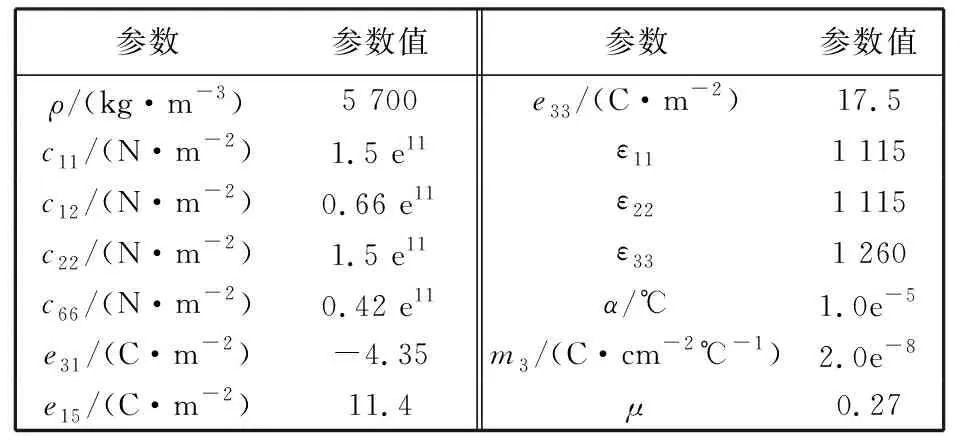
表 1 钛酸钡材料参数[14]

进行模态分析时， 结构的模态参数由下式求解

([D]-ω2[M]){K}=0,

(16)

式中： [D]为刚度矩阵； [M]为质量矩阵； {K}为模态矩阵. 由于质量矩阵一般不受温度的影响， 由式(16)看出， 温度引起结构模态频率和振型的变化主要是结构的刚度变化导致的. 温度升高会引起钛酸钡陶瓷的杨氏模量和介电常数发生变化[15].

本文使用ANSYS 14.0对压电材料矩形板进行有限元建模与仿真， 通过模态分析得出矩形板的固有频率及振型. 模型采用SOLID5单元进行分析. 矩形板长为300 mm， 板厚为10 mm， 分别置于70, 90, 110 ℃的恒定温度场下， 当宽b分别为200, 230， 250， 300 mm时， 由ANSYS仿真得到前三阶固有频率， 其对应结果如表 2.

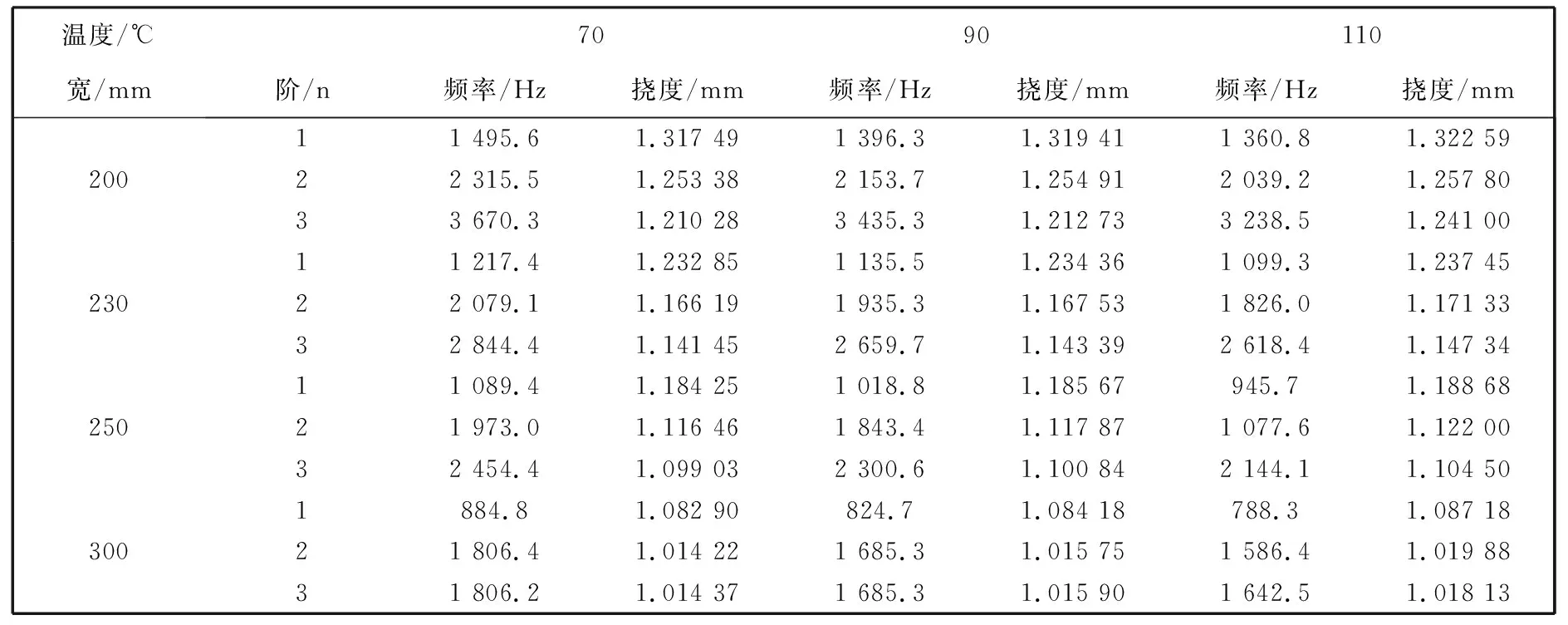
表 2 前三阶固有频率和挠度

从表 2 可以得出结论： 随着宽度的逐渐增大， 长宽比减小， 恒定温度场中四边简支的压电材料矩形板的挠度和固有热振动频率都减小. 随着温度升高， 恒定温度场中矩形板的固有热振动频率减小， 挠度增大. 文献[16]中温度对普通弹性板固有频率和振幅的影响， 文献[17]中宽度变化对压电层合板的固有频率的影响， 均与本文结论一致， 故本文的方法和结论具有可靠性.

3.2 谐响应分析

在模态分析的基础上， 对在70 ℃的恒定温度场下， 长a=300 mm， 宽为b=300 mm， 板厚h=10 mm的压电材料矩形板采用Full方法进行ANSYS谐响应仿真分析. 取材料阻尼比为0.01， 在压电材料矩形板的上表面施加2 MPa频率为 850 Hz 的余弦简谐力作为激励载荷， 在 700～1 200 Hz 的频率范围内取50个子载荷步， 采用Sparse solver求解器进行求解， 得到在恒定温度场下压电材料矩形板最大应力节点处z方向的幅频曲线以及外激励对应力幅值的影响.

外激励频率对板横向振动的影响如图 2 所示. 由图 2 可知， 当外激励频率远小于885 Hz时， 矩形板横向位移较小， 横向位移激振力频率在相位上提前180°； 当外激励频率等于基频时， 矩形板的横向位移急剧增大， 且比激振力频率在相位提前90°， 即将达到共振状态； 随着外激励频率继续增大， 离开共振区的矩形板的横向位移幅值迅速减小， 此时横向位移与激励力在相位上几乎相同.

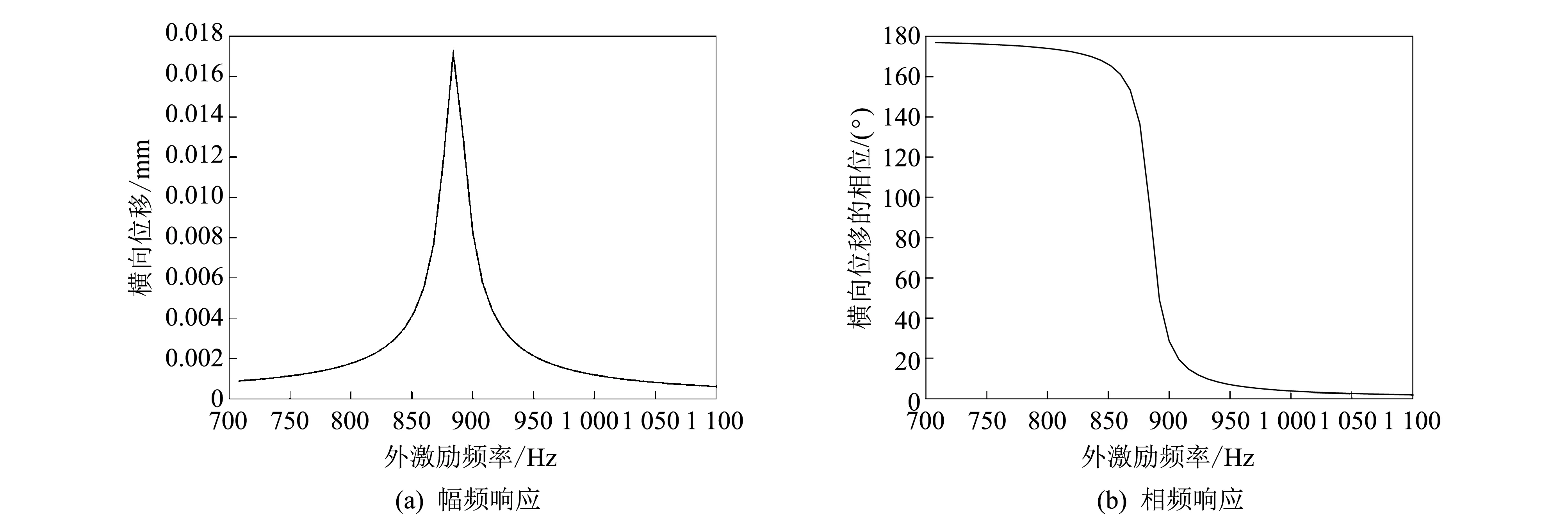
图 2 外激励频率对板横向振动的影响Fig.2 Influence of external excitation frequency on transverse vibration of plate

图 3 所示为外激励频率对板z方向应力的影响. 由图 3 可知， 当外激励频率远小于885 Hz时， 矩形板横向应力较小， 横向应力与激励力在相位上几乎相同； 当外激励频率等于基频时， 矩形板的横向应力振幅急剧增大， 且比激振力频率在相位提前85°， 即将达到共振状态； 随着外激励频率继续增大， 离开共振区的矩形板的横向应力幅值迅速减小， 此时横向应力与激励力在相位上几乎相同.

图 3 外激励频率对板z方向应力的影响Fig.3 Influence of external excitation frequency on the stress of z direction

由图2(a)和图3(a)可看出横向振动位移和z方向应力幅值变化趋势一致， 即横向位移越大， 内部的应力幅值也越大. 当达到共振时， 横向位移和应力响应的幅值急剧增大， 但并未无限放大， 是因为阻尼对响应峰值具有抑制作用. 故阻尼的设置能较好地抑制结构的振动响应.

3.3 温度对横向位移的影响分析

为了分析温度对横向位移的影响， 通过ANSYS软件对压电材料矩形板进行瞬态响应分析， 运用完全法， 取阻尼比为0.01， 在矩形板上表面施加2 MPa频率为300 Hz的余弦简谐力， 得到不同恒定温度场下四边简支的压电材料矩形板最大应力节点1 981的横向位移时程曲线， 如图 4 所示.

图 4 温度对矩形板横向位移的影响Fig.4 Effect of temperature on transverse displacement of rectangular plate

由图 4 可知， 在不同恒定温度场的简谐激振力作用下， 节点1 981的运动较为混乱， 振动情况也比较复杂. 图 4 表示外激励的频率远小于共振频率时横向振动的位移变化， 可以看出， 随着时间的增加， 振动情况都将趋于稳定. 而总体上节点是围绕平衡位置进行周期振动的， 温度越高， 其横向位移越大， 这主要是因为简谐激振力一定的情况下， 温度升高这会降低结构的刚度， 抵抗荷载作用下的变形能力减弱； 且随着时间的增加， 其振幅在阻尼的影响下有明显的衰减特征.

3.4 薄板最大应力节点的应力响应分析

在以上分析的基础上， 对薄板上表面施加2 MPa 频率为300 Hz的余弦简谐力作为激励载荷的情况进行具体分析， 得到矩形板最大应力节点处横向速度， 横向加速度以及最大应力在0.3 s内的时程曲线， 如图 5(a)～(c) 所示.

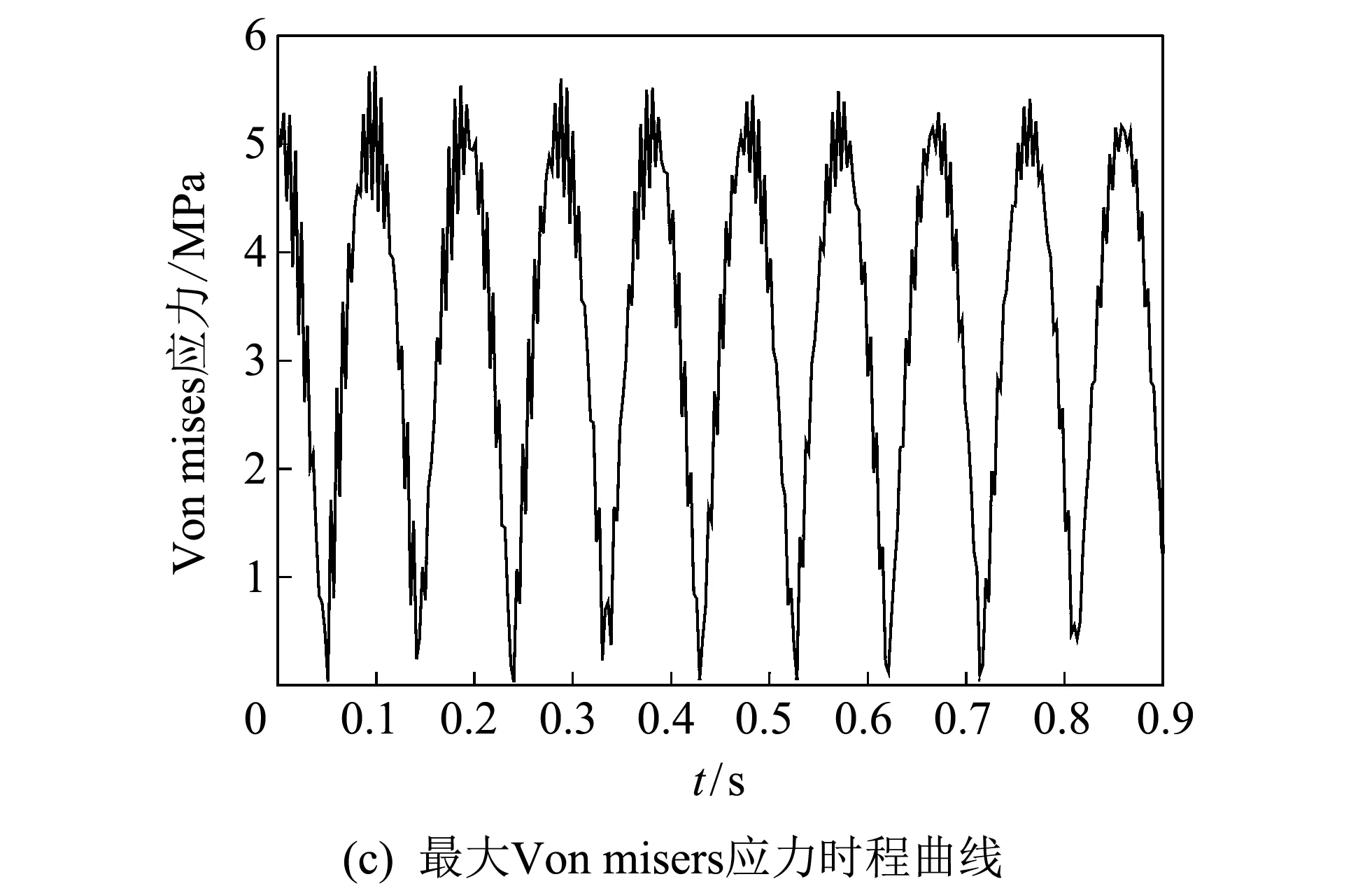
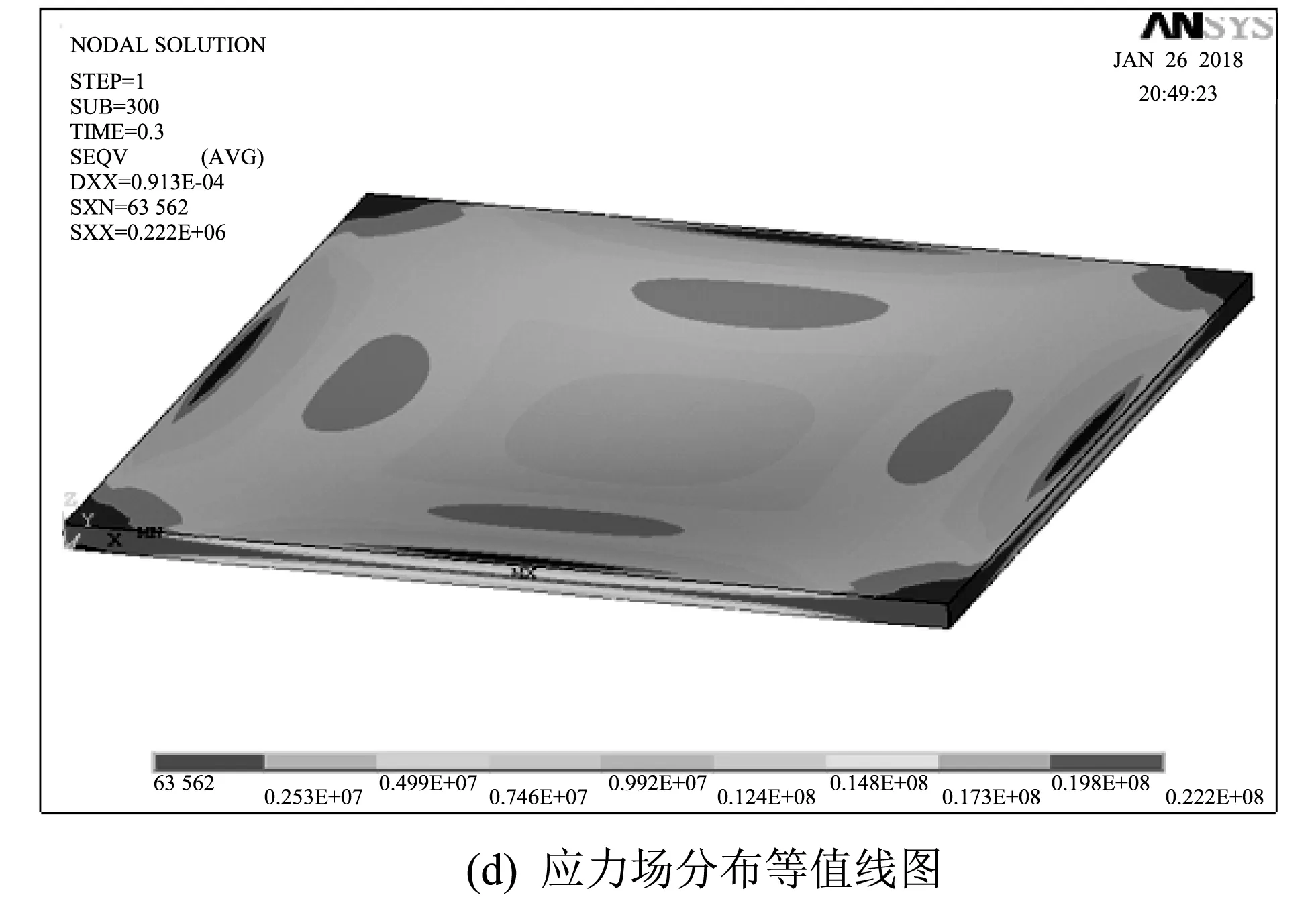
图 5 最大应力节点的响应分析

由图 5(a)和图 5(b)可看出， 在简谐外力的激励作用下横向速度和横向加速度的时程曲线呈现规律性的变化， 为振幅逐渐减小最终趋于稳定的简谐曲线， 其振动频率为简谐力的激振频率. 图 5(c) 为最大应力处节点1 981的Von misers应力时程曲线， 可看出此节点在稳定阶段应力幅值在0.005 2～5.206 8 MPa间变化， 且位移响应幅值越大， 应力值也越大. 四边简支的压电材料矩形板在受到恒定温度场和简谐力的激励下做强迫振动时， 其最大应力位置出现在板的边缘位置， 如图 5(d) 所示. 因此在实际应用中， 应针对此类现象采取相应的解决方法和对应措施.

4 结 论

本文对恒定温度场下受简谐激振力作用的压电材料矩形板的频率和振幅进行了分析， 结论如下：

1) 计算结果表明： 温度、 矩形板的长宽比和外激励对板的动力响应均有一定的影响， 长宽比减小， 弯曲挠度和固有振动频率都减小. 温度升高， 固有振动频率减小， 弯曲挠度增大.

2) 当外激励频率等于矩形板的固有振动频率时， 达到共振状态， 矩形板的横向振幅和z方向的应力值急剧增大， 且均比激振力频率在相位提前90°.

3) 温度场对横向位移的影响非常明显， 温度越高， 其横向位移越大.

4) 振动时最大应力位置出现在薄板的边缘位置， 薄板横向位移越大， 应力值越大. 当外激励的频率等于压电材料矩形板的固有频率时， 会达到共振状态， 此时的振幅最大， 在工程实际中会造成极大的危害.