基于Mirosot平台改进遗传算法避障策略

孙绍华， 王魁生， 张恬恬

(西安石油大学 计算机学院， 陕西 西安 710065)

0 引 言

Mirosot机器人平台一般由视觉子系统、 通信子系统、 决策子系统以及机器人子系统4部分组成， 其决策系统如何根据视觉系统采集到的障碍物信息并结合实际的机器人状态进行合理的路径规划是非常重要的.

机器人避障路径规划一般可以分为两级： 全局规划和局部规划， 即整体目标分解为局部目标， 再由局部规划实现局部目标. 与此同时需满足各种约束条件： 路径最短、 躲避障碍、 经过设定点、 耗时最短等[1]. 但是不同的算法在解决问题的过程中具有不同的侧重.

文献[2]认为机器人决策应该产生平滑的路径以避免机器人反复停止和重新开始所造成的损耗， 提出了利用改进的蜂群算法结合三次贝塞尔曲线进行路径规划的解决方案. 文献[3-5]在对比人工势场法和遗传算法的基础上， 更加侧重路径规划的时间和空间复杂度优化， 提出基于模糊控制的机器人避障路径算法， 并在结论处提出可以采用集成算法结合各个算法优势进一步改进路径规划问题. 文献[6]提出基于遗传算法的机器人避障路径规划算法， 该算法基于阶段性路径实现思路进行设计. 文献[7]认为蚁群算法在复杂环境下进行路径规划时存在问题， 因此设计了一种新的动态搜索诱导算子以改进蚁群算法性能. 文献[1，8]提出改进粒子群算法实现机器人路径规划， 并且注重优化算法的实时性， 保证路径规划的效率. 文献[1]将粒子群算法与遗传算法相互结合提出交叉算子和变异算子实现机器人路径规划算法的快收敛和高效率. 文献[8]提出一种结合Ferguson样条描述和改进粒子群优化算法的路径优化方法， 将路径规划问题转化为三次样条曲线参数优化问题， 借助改进的具有速度变异的粒子群算法进行路径优化.

通过研究上述文献， 发现基于Mirosot平台机器人路径规划算法的设计均忽略机器人自身构造的影响， 并且未考虑机器人在带球情况下的路径规划问题， 致使在实际应用环境中单独机器人避障效果较好， 但却无法完成带球避障路径规划， 反复出现丢球等现象.

综上所述， 本文结合机器人构造提出限制角度δ， 设计适应值因子wk， 改进文献[6]中的遗传算法， 设计机器人带球避障路径规划算法， 并对改进算法进行实验验证.

1 外观构造限制条件

Mirosot半自主型机器人要求每个机器人尺寸不能超过7.5 cm×7.5 cm×7.5 cm， 如图 1 所示. 球体为直径为42.7 mm的高尔夫球. 比赛要求机器人抓球或持球不能超过球体体积的30%， 见图 2. 由于机器人球槽包含两侧， 本文仅进行单侧分析， 另一侧同理.

图 1 机器人效果图Fig.1 Robot design sketch

图 2 持球尺寸限制Fig.2 Size limit of holding the ball

根据比赛规则要求， 机器人持球深度不能超过12.81 mm.

42.7×30%=12.81.

(1)

如图 3 所示， 机器人在带球运动过程中， 根据球体直径以及机器人尺寸计算得出， 球体与机器人接触实际深度为11.14 mm.

(2)

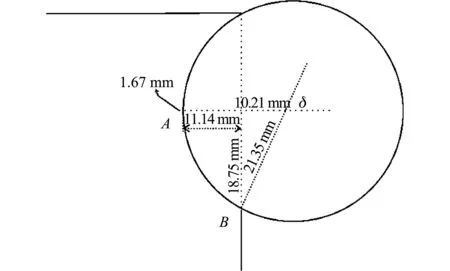
图 3 持球尺寸标注Fig.3 Dimensioning of robot

按照比赛规则设计的机器人在进行带球运动时， 无法满足机器人和球体接触的极限深度12.81 mm， 即30%， 机器人与球体接触的实际最大深度为11.14 mm， 即26%， 见图 4.

(3)

在实际机器人带球避障过程中， 如果机器人旋转角度超过δ， 则会造成球体脱离， 即δ为机器人带球运动时的旋转限制角.

图 4 实际尺寸Fig.4 The actual size

2 设计适应值函数

根据文献[6]遗传算法中所提出的适应值函数， 结合上文中结论， 对适应值函数进行改进， 使算法选取的路径点满足机器人旋转限制角条件.

首先， 以目标点G和初始点S建立搜索范围空间， 假设SG之间距离为L， 以L为长，L/2为宽做一矩形， 矩形内机器人为障碍点， 如图 5 所示.

图 5 避障路径搜索空间Fig.5 Obstacle path search space

其中， 以Pk=(x(k),y(k)),k=1,…,n表示路径点， 以ORj，j=1,…,q表示障碍物机器人， 取障碍物机器人中心点(xj,yj)表示障碍物位置，r表示以机器人为中心点的圆的半径.

则改进后适应值函数如下

fi=uk+vj,k+wk,

(4)

(5)

(6)

(7)

式(4)中：fi为第i条路径的适应值大小，uk表示路径点k躲避障碍物的程度，vj,k表示路径点k与障碍物j之间的距离大于机器人半径r的程度，wk表示路径点k满足转向角度δk∈δ的程度.

式(5)中：Lk为路径点k至目标点G在SG上的距离，lk为路径点至目标点G的距离， 如图 6 所示，α表示路径点规避障碍物程度在适应值函数中所占比重.

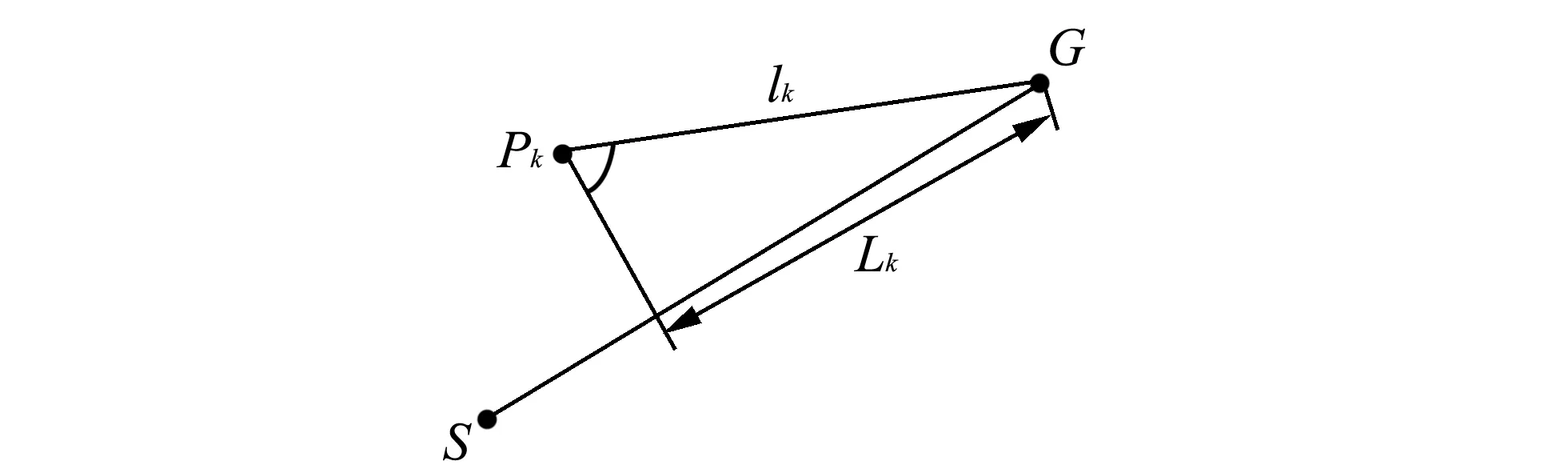
图 6 路径点接近程度Fig.6 Path point proximity

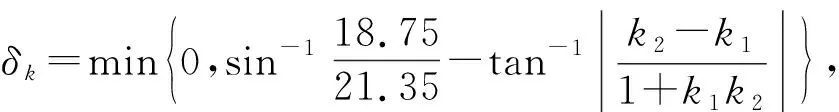
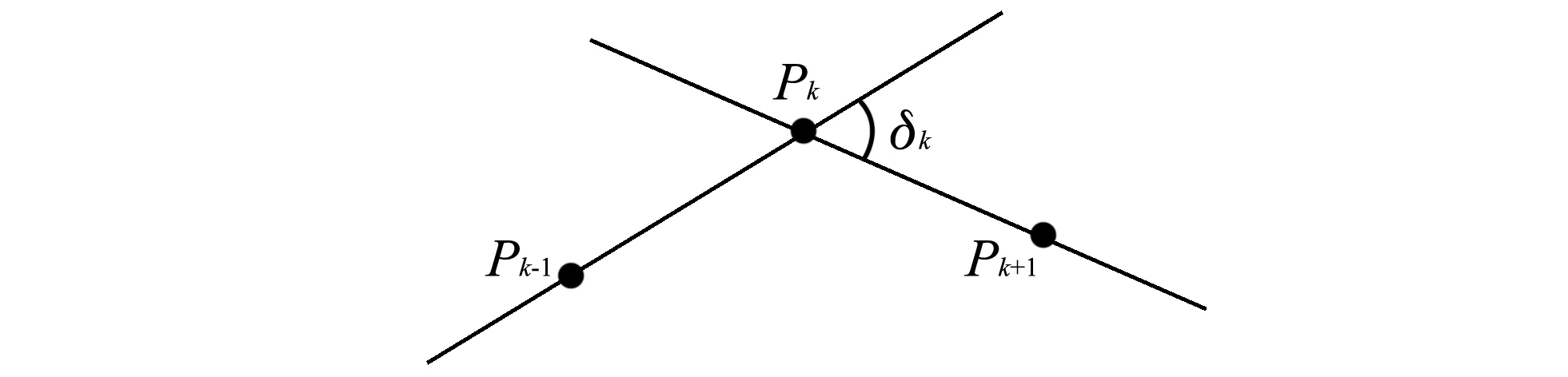
图 7 旋转角度限制Fig.7 Rotation Angle limit

3 改进遗传算法

根据文献[6]中的遗传算法设计， 步骤如下：

1) 首先进行路径编码， 将场地路径点变为染色体编码.

2) 选择合适的路径群体数目M， 交叉概率pc和变异概率pm.

3) 随机产生一个初始群体M.

4) 利用适应值函数fi计算每条路径的适应值大小， 进而求出适应值总和F=∑fi，i=1,…,M.

6) 按照预先设定的交叉概率进行交叉.

7) 按照预先设定的变异概率进行变异.

8) 判断是否满足条件， 满足则执行， 不满足则继续迭代.

本文基于上述算法步骤， 结合前文结论所改进的适应值函数fi， 实现机器人带球避障路径规划.

4 实 验

根据上述算法步骤， 分别对单独机器人带球避障效果和整体比赛效果进行实验验证. 将本设计算法应用于Mirosot机器人3V3场地平台上， 编程环境为Microsoft Visual C++ 6.0.

实验一： 设置3个静态机器人障碍物， 1个带球避障机器人， 如图 8 所示. 原算法和改进算法各进行30次实验， 共计60次实验， 实验结果如表 1 所示.

图 8 静态避障Fig.8 Static obstacle avoidance

表 1 实验1结果

表 1 数据表明， 原算法无法实现机器人带球避障， 改进后带球避障成功率为53.3%， 有效提升了带球避障成功率.

实验二： 进行3V3机器人对抗赛， 双方各3名机器人为参赛队员， 其中1名为守门员， 其余2名为攻守队员， 如图 9 所示. 上下半场各比赛 5 min， 蓝方为原算法实现的带球避障效果， 黄方为改进算法后实现效果， 实验结果如表 2 所示.

图 9 动态避障Fig.9 Dynamic obstacle avoidance

表 2 实验2结果

全场比赛共计10 min(600 s)， 蓝方(原算法)全场带球时长为145 s， 占比24.17%； 黄方(改进算法)全场带球时长为455 s， 占比75.83%. 带球时长数据表明， 黄方在控球时间上处于绝对优势地位. 全场总进球数为6， 其中蓝方进球数为1， 黄方进球数为5， 最终比赛黄方获得胜利.

5 结 论

本文综合前人的研究成果， 引入机器人外观构造变量， 在原有遗传算法的基础之上设计机器人带球避障遗传算法， 并提出了机器人旋转角度限制条件δ和适应值因子wk.

设计单独机器人带球避障和整体比赛效果两个实验对算法进行验证， 实验结果表明， 改进算法的带球避障成功率提升了53.3%， 比赛控球时间占比为75.83%， 并最终以进球数的绝对优势取得比赛胜利.

本文采用阶段性路径规划算法， 即遗传算法进行研究， 在实验中如文献[2]所述， 机器人出现明显的抖动情况， 这也是影响带球效果的主要原因， 在未来的研究中可以将旋转角度限制因子引入蜂群等连续性路径规划算法中进行改进.