深广神经网络在变压器故障诊断中的应用

杜 江， 张知杰， 孙铭阳， 吕艳硕

(1. 河北工业大学 省部共建电工装备可靠性与智能化国家重点实验室， 天津 300130； 2. 河北工业大学 河北省电磁场与电器可靠性重点实验室， 天津 300130)

0 引 言

变压器作为供电系统中的枢纽设备， 对整个电力系统的安全经济运行至关重要， 因此有必要对变压器进行故障预诊断[1-2]. 传统的变压器故障预诊断多采用周期性停电人工检修的方法， 该方法有很大的不足， 其一是需要停电操作； 其二是诊断准确率直接依赖于检修人员的工作经验.

近年来， 随着科学技术的进步和计算机水平的提升， 越来越多的人工智能算法被广泛应用于变压器故障诊断领域， 如专家系统[3]、 神经网络[4]、 支持向量机[5]、 免疫识别[6]、 模糊理论[7]、 聚类分析[8]等. 油中溶解气体分析(Dissolved Gas Analysis, DGA)[9]技术是目前常用的一种变压器故障诊断技术， 该技术可以在不停电的情况下实时采集变压器的DGA数据， 通过分析找出变压器油中气体含量与故障类型之间的联系， 而后对变压器进行故障诊断. 变压器油中气体含量(故障特征)和故障类型(诊断结果)之间的关系是非线性的， 而神经网络算法常被用来处理非线性问题.

目前常见的神经网络， 如浅层BP神经网络在对样本进行训练时有一定的缺陷， 当要解决的问题为求解复杂非线性函数的全局极值时， BP算法作为一种局部搜索的优化算法， 很有可能陷入局部极值， 使训练失败， 同时更容易出现过拟合问题[10]. 因此学者提出了多种改进神经网络算法[11-13]， 并成功地应用在变压器的故障诊断中. 现有对神经网络算法的改进集中在对训练模型的参数优化部分， 不能同时实现对历史数据的记忆能力和对未知数据的泛化能力， 且很少考虑故障特征之间交互对诊断结果的影响， 对此本文的改进点如下：① 提出一种基于深广神经网络算法Deep & Wide Model， 简称为DWM)[14]的故障诊断方法， 将深度学习和线性模型的优势相结合； ② 引入交叉特征来挖掘特征之间的内在联系和潜在特征. 实验在变压器的DGA数据上与多种方法进行对比， 证明所提方法诊断结果更精确.

1 深广神经网络基本原理

对变压器的故障诊断是一个分类过程， 主要关注如何同时实现模型的记忆能力和泛化能力. 记忆能力可以理解为从历史数据中学习特征之间的共现性以及这些特征之间的相关性， 基于历史数据的规律对新的样本进行分类预测， 然而单纯的记忆能力存在很大的局限性， 比如在变压器故障诊断中， 有一组离散特征数据A和B， 历史数据中只存在A为1且B为1的情况而不存在A为1且B为0的情况， 单纯的记忆能力基于历史数据就不能学习到A为1且B为0时的分类结果， 无法对新出现的特征组合进行分类. 泛化能力则是依据特征相关性的传递特性去挖掘一些历史数据中没有出现过的特征组合， 上文中A为1且B为1与A为1且B为0这两个特征组合很相似， 因此特征之间的相关性也会彼此传递， 基于传递性的学习能够提高系统分类结果的多样性， 但又可能做出不准确的分类， 出现在训练数据上过拟合的现象. 因此将二者结合， 联合训练用于实现记忆能力的广义线性模型和用于实现泛化能力的深度神经网络模块， 得到一个用于对变压器进行故障诊断的DWM模型， 如图 1 所示.

图 1 DWM模型Fig.1 The structure of deep and wide neural network

1.1 深度神经网络模块

深度模块是一个前向神经网络， 如图 1(c) 所示. 它的输入是归一化后的DGA数据. 神经网络的具体工作流程见图 2， 它包含： 输入层、 多层隐藏层和输出层. 图中每个节点代表一个神经元， 它的输入输出关系为

(1)

式中：xi为神经元的输入值；wi为权重值；b为偏差；y为神经元的输出值；f为激活函数， 在本次实验中选择ReLU函数， 形状见图 3， 表达式为

Φ(x)=max(0,x),

(2)

式中：x为隐藏层的节点值.

图 2 深度神经网络模块的工作流程图Fig.2 Work flow chart of the deep neural network module

ReLU函数具有单侧抑制、 兴奋边界相对宽阔、 激活性稀疏等特点， 与人神经皮层的工作原理接近， 故选用该函数作为中间隐藏层节点的激活函数.

图 3 ReLU函数的形状图Fig.3 The shape of ReLU function

1.2 广义线性模型

广度模块是一个广义线性模型， 如图 1(a) 所示. 它的具体工作过程如图 4 所示， 输入为向量X={x1,x2,…,xd}T,Φ(x)={φ(X)1,φ(X)2,…,φ(X)t}T，xi为离散数据，φ(X)j为交叉积转换后的特征， 目的是为了实现特征组合， 转换公式如下

(3)

式中：cti为一个布尔型的变量， 当第i个特征是第t个转换φt的一部分时， 它的取值是1， 其它时候则取0. 对于二进制离散特征， 只有当两个特征的取值同时为1时， 它们的交叉积转换才能取值为1， 其它时候则取0. 该式描述的是特征之间“与”的关系， 表征了关联的特征对共同出现的型态. 这种方法能捕捉到二进制离散特征间的交互， 为广义线性模型增加非线性. 输出层的计算公式为

Y=X·W1+Φ(X)·W2+b,

(4)

式中：X为离散特征向量；Φ(X)为交叉积转换特征向量；b为偏差；Y为输出向量.

图 4 广义线性模型结构Fig.4 The structure of the generalized linear models

1.3 联合训练

联合训练与集成训练是有区别的， 集成训练是两个模型单独训练， 只在最后对二者的输出进行合并， 且因模型之间相互独立， 训练单个模型需要更多的特征和工程来满足所需的精度； 联合训练则是通过优化同一个损失函数来将两个模块的参数同时更新. 将上述深度神经网络模块和广义线性模块共同输入到softmax层[15]， 计算分类结果. 具体的softmax函数公示如下

∀i∈1,…,C.

(5)

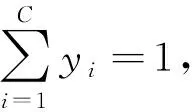
采用图 1(b) 所示模型， 将深度神经网络和广度模块的输出进行加权求和， 然后将其输入到softmax层中完成对故障类型的分类. 模型的输出公式如下

P(Y=1|X)=

(6)

式中：Y为一个多值的类别标签；X为离散特征向量；Φ(X)为交叉积转换特征向量；alf为深度模块隐藏层最后一层的输出向量；Wdeep为深度模块的权重向量；Wwide为广度模块的权重向量；b为偏差，Wdeep,Wwide和b这3个参数在训练开始被随机初始化为[-0.1,0.1]的均匀分布；σ为上述softmax函数.

2 基于深广神经网络的变压器故障诊断模型构建

2.1 样本收集

2.2 数据预处理

2.2.1 连续特征离散化

离散化的优点体现在： ① 广度部分模型表达能力有限， 将单变量扩展成N元变量， 每个变量有单独的权重， 能够提升模型的表达能力； ② 离散化后可以进行特征交叉， 为模型引入非线性， 进一步提升模型的表达能力.

连续特征的离散化采用等宽分箱法， 假设特征的取值空间为X={x1,x2,…,xn}， 离散化之后的类标号为Y={y1,y2,…,ym}， 即将X等宽划分到m个区间中. 在本次试验中， 根据DGA数据每种特征的取值范围不同， 设定不同的区间宽度k， 那么对于每个xi， 对应的离散值计算公式为

(7)

2.2.2 离散特征独热编码

独热编码又称一位有效编码， 其方法是使用N位状态寄存器来对N个状态进行编码， 每个状态都有它独立的寄存器位， 并且在任意时候， 只有一位有效. 例如对样本中的6种故障类型进行编码， 其自然编码为1， 2， 3， 4， 5， 6； 其独热编码为000001， 000010， 000100， 001000， 010000， 100000. 即对于每一个离散特征， 如果它有N个可能值， 那么经过独热编码后， 就变成了N个二元特征， 并且这些特征互斥， 每次只有一个激活.

2.2.3 交叉特征构建

在线性建模过程中， 基本特征是对全局进行建模， 特征交互则是对独立特征做向量积， 这样做可以使特征更加精细， 比如两个特征A和B， 在没有特征交互的情况下是独立的特征， 但有了AB特征交互， 可以发现AB特征共同出现对分类起了很关键的作用. 特征交互可以看做是个性化的体现， 使得特征兼顾全局和个性化， 同时也为模型增加了非线性.

本次实验中， 将连续型DGA数据离散化后进行特征组合. 如((H2>0 和 H2<10) and (CH4>30 和 CH4<40))=1， 表示当H2和CH4的含量同时处于某个给定区间时， 对应的二者交叉特征取值为1， 否则为0， 交叉特征的引入可以捕捉到H2含量和CH4含量之间的特征关联.

家禽感染大肠杆菌可能与原发因素有关，也可能是因为家禽自身抵抗力持续降低。而在因大肠杆菌引发的众多病症中，气囊炎有着较高的发病率［2］。家禽初发该病症时没有明显症状，因此很容易被养殖户所忽视，但是待病症发展到较为严重的阶段，就会导致家禽出现呼吸窘迫、咳嗽等症状，不利于家禽正常呼吸，甚至还会导致家禽死亡。

2.2.4 连续特征归一化

深度神经网络模块需要对输入的DGA数据进行归一化， 避免在训练过程中出现梯度爆炸或者梯度消失的现象， 提升深度模块的训练速度.

本次实验中采用极差法对DGA数据进行归一化， 将原始数据缩放至[0,1]范围内， 计算公式如下

(8)

2.3 DWM结构构建

DWM的结构如图 1 所示， 本次实验中深度模块包括： 输入层、 隐藏层和输出层. 隐藏层设置为两层， 每一层的节点数目分别为64， 32； 广度模块是一个逻辑回归模型. 上述两个模块用同一个softmax函数进行分类计算， 用同一个损失函数进行参数更新. 损失函数设定为交叉熵损失， 其公式如下

(9)

式中：n为样本数；m为类别数；z为期望的输出；a为神经元实际输出， 当实际输出a与期望输出z接近时， 损失函数接近于0， 如z=0,a～0;z=1,a～1时， 损失函数都接近于0， 函数性能很好. 试验采用的交叉熵损失函数具有非负性， 因此通过最小化损失函数来使得实际输出与期望输出更接近.

在实验中， 使用批量梯度下降法(Batch gradient Descent， 简称为Bgd)更新网络参数. 在每一轮的训练过程中， Bgd用一批数据计算损失函数的梯度， 从训练集中随机抽取样本， 每一批所抽取的样本大小为64， 并基于此在反向传播过程中对参数进行优化更新， 赋值公式如下

(10)

(11)

式中：wl为第l层的权重；bl为第l层的偏置量；η为神经网络学习率.

实验开始前对参数初始化， 所有的权重和偏差参数初始化为[-0.1,0.1]的均匀分布， 神经网络的学习率为超参数， 通过人工调节设定为0.001.

3 变压器故障诊断实验和对比

本次实验的硬件平台： 操作系统为Windows7旗舰版. 数据来源于文献[16]， 将文献附录中的样本按5∶1分成训练集和测试集， 训练中有500组数据， 测试集包含100组数据. 将训练样本进行数据预处理后分别用深广神经网络、 逻辑回归、 浅层BP神经网络和支持向量机进行训练， 然后用测试集对训练好的4种模型分别进行测试， 并对测试结果进行比较.

3.1 基于深广神经网络的实验流程

基于DWM的变压器故障诊断流程如图 5 所示. 步骤如下：

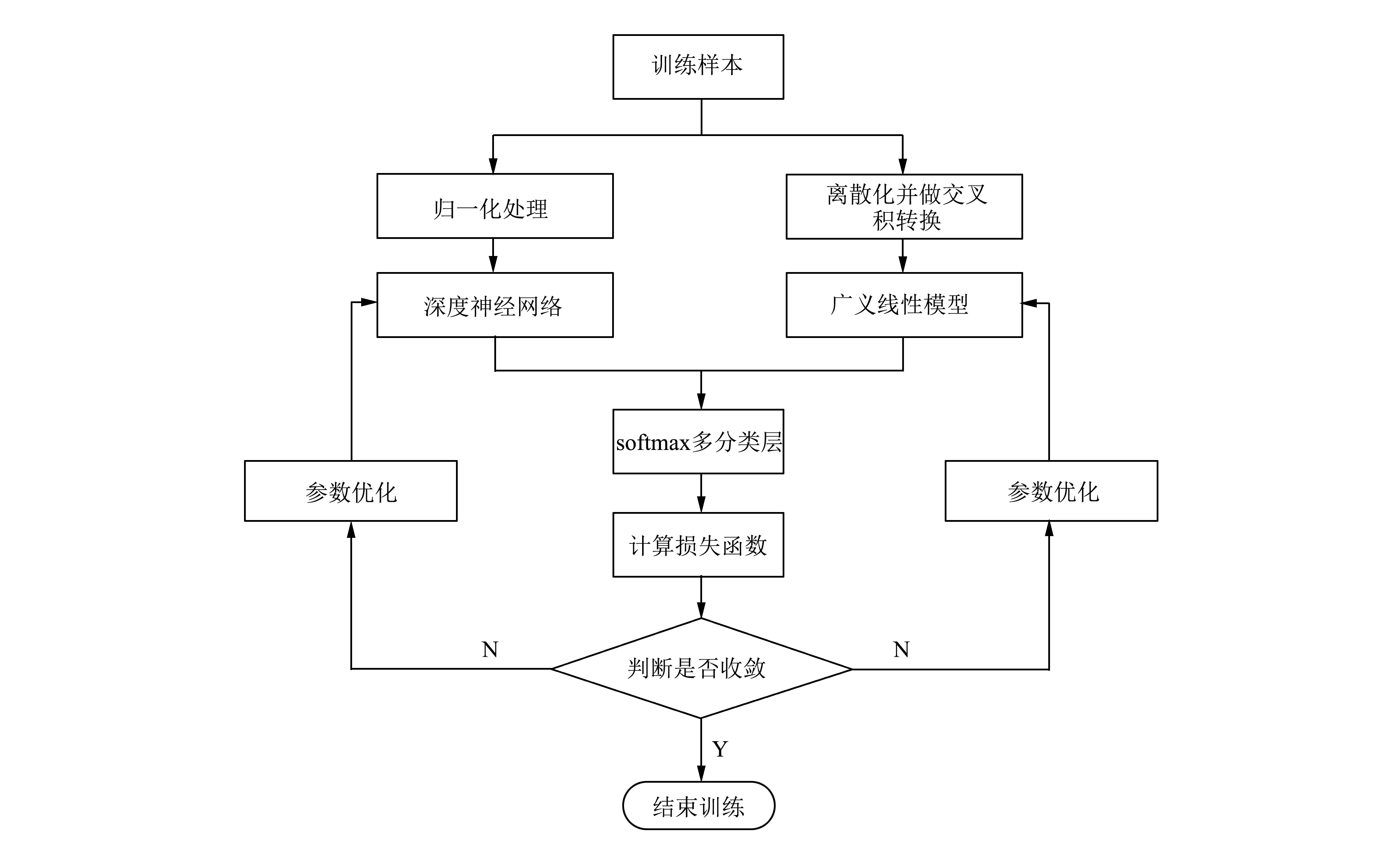
图 5 DWM训练流程图Fig.5 Training flowchart of DWM

1) 数据预处理.

待处理的数据为连续型的DGA数据.

① 连续特征归一化， 作为深度神经网络模块的输入；

② 连续特征离散化， 对离散化特征独热编码， 并做交叉积转换实现特征组合， 共同作为广义线性模型的输入.

2)深度模块隐藏层设置为两层， 各层的节点数目分别为64, 32.

3)神经网络参数初始化为[-0.1,0.1]内的均匀分布， 并将神经网络的学习速率调节为0.001， 每一批样本数量为64.

4)将深度神经网络模块和广义线性模型联结， 构建神经网络.

5)训练神经网络.

6)判断模型是否收敛. 如果模型在训练集中的损失下降， 而在测试集中的损失上升， 表明再训练下去会过拟合， 这时可以停止训练， 否则使用批量梯度下降法优化参数后， 返回步骤5)继续训练.

3.2 对比实验

1) 基于径向核函数构建的支持向量机(SVM)二分类器来构建多分类器. 采用一对多法， 训练时把样本特征归一化， 挑出某一故障类型的样本作为正例， 其他剩余的样本作为负例， 6种故障类型就构造出6个SVM， 将未知(测试)样本分类为分类函数数值最大的那种故障类型.

2) 逻辑回归(Logistic Regression， 简称为LR)， 用预处理后的训练集对模型进行训练， 直至收敛. 用训练好的模型对预处理后的测试集进行预测， 并与实际故障类型进行比较， 计算准确率.

3) BP神经网络(BP Neural Network， 简称为BPNN)包含一层输入层， 两层隐藏层， 一层输出层， 隐藏层的节点数目分别为64， 32. 权重和偏差参数初始化为[-0.1,0.1]的均匀分布， 学习率为超参数， 设定为0.001， 每一批样本数量为64， 对预处理后的训练集进行训练， 直至模型收敛. 用训练好的模型对预处理后的测试集进行预测， 并与实际故障类型进行比较， 计算准确率.

上述4种方法的训练结果如图 6 所示； 用测

试集对4种模型进行测试， 测试结果见表 1. 在样本容量较大且数据庞杂时， 由图6可以看出， LR和SWM的训练结果较差， 准确率分别为75%和70.4%； BPNN在训练刚开始时准确率波动较大， 甚至低至30%左右， 在后期随着训练次数的增长， 准确率有所提升且趋于稳定， 最高也仅有72%， 训练结果不理想； DWM的准确率随着训练次数的增长而提升， 过程平缓且很快趋于稳定， 训练收敛时的准确率约为84%， 相较于其他3种算法有明显的提升. 表 1 将4种算法对测试集的测试结果进行了对比， DWM的诊断准确率明显高于其他3种算法， 对变压器的故障诊断意义重大.

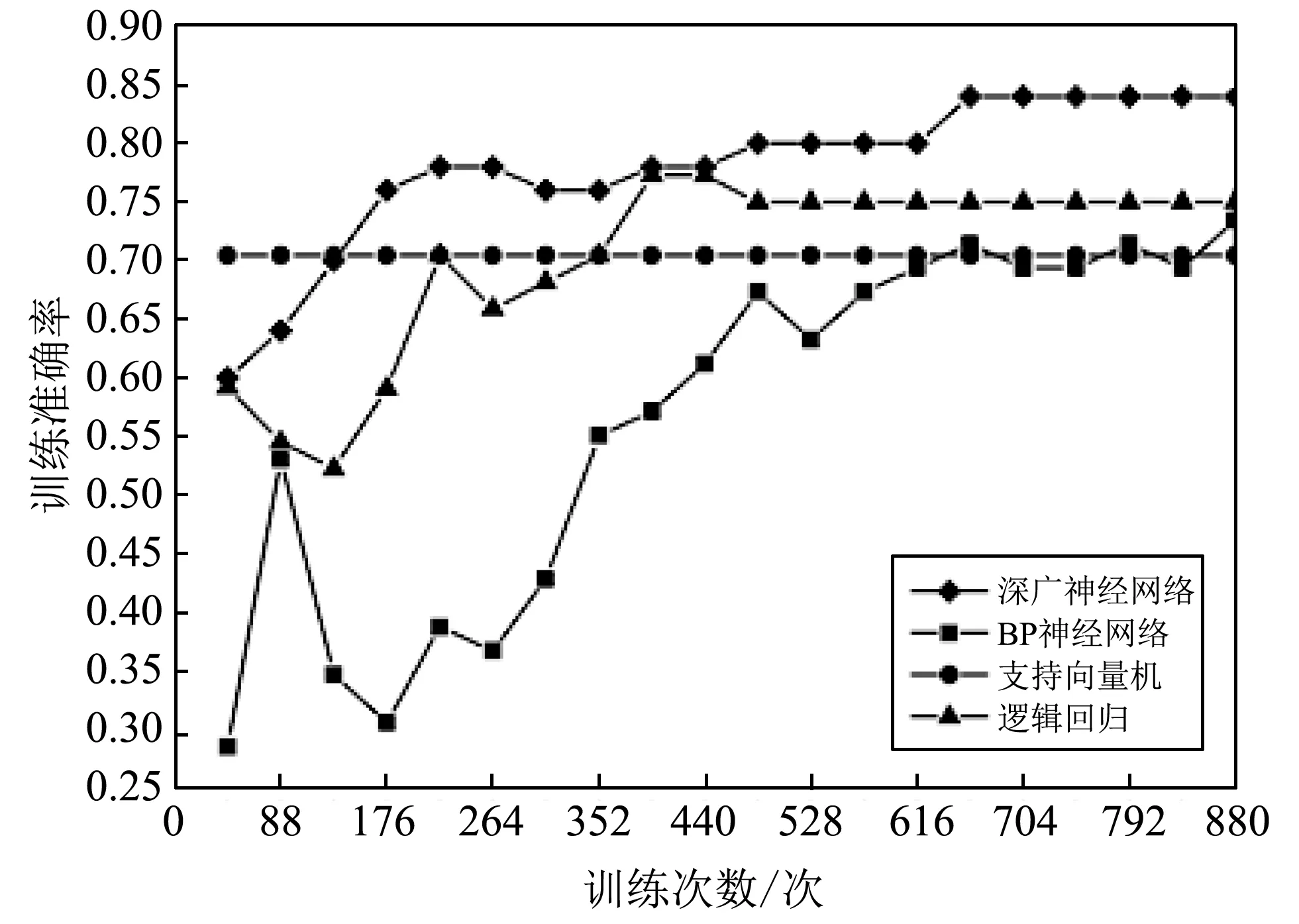
图 6 4种算法的训练结果Fig.6 The training results of four algorithm

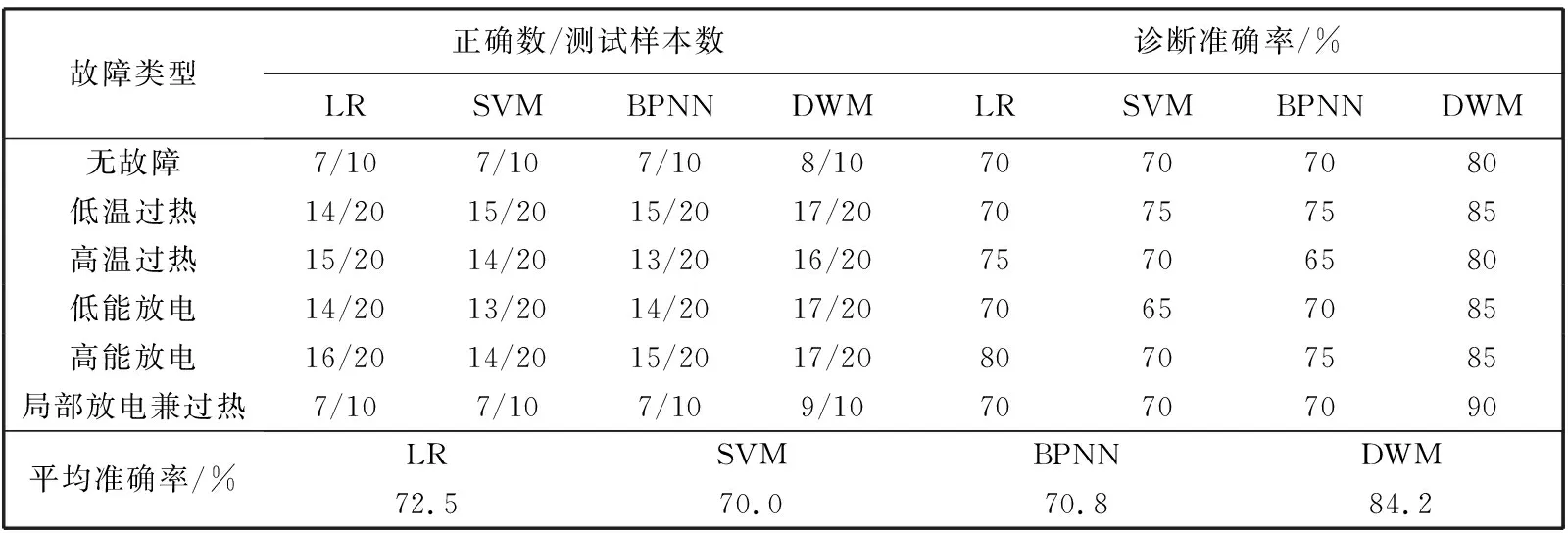
表 1 4种算法的诊断结果

4 结 论

本文提出一种基于DWM的变压器故障诊断方法， 将能够实现记忆能力的广义线性模型和用来实现泛化能力的深度神经网络模型结合， 同时引入了交叉特征， 考虑了特征数据的交互对变压器故障诊断结果的影响. 用DWM模型训练预处理后的训练集， 在反向传播过程中采用批量梯度下降法对DWM进行参数优化， 通过优化同一个损失函数来实现两个模块参数的同时更新. 用训练好的模型对测试集进行故障诊断， 并将诊断结果与其他3种算法进行对比， 对DWM的诊断效果进行了验证. 实验结果证明， 相较于其他3种算法， DWM具有更好的挖掘能力， 诊断准确率更高.