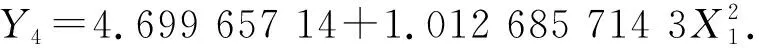基于均匀设计的自蔓延切割装置喷嘴研究

阚润哲 ， 成泓进， 张树海 ， 苟瑞君 ， 陈亚红

(1. 中北大学 环境与安全工程学院， 山西 太原 030051； 2. 太原市公安局， 山西 太原 030001)

0 引 言

自蔓延切割装置是近年来国内开始研究的新型切割工具， 该装置基于自蔓延高温合成技术研制， 可以依靠高热剂的自蔓延高温燃烧反应产生的熔融金属及金属氧化物对要切割的金属材料进行融化、 冲击以实现切割， 具有无需外接能源及设备、 小巧便捷、 操作简单、 切割效率高等特点[1-3]. 因此该装置可以在复杂环境下完成切割工作， 诸如废弃弹药销毁、 战场抢修、 自然灾害救援等.

1972年美国学者Helms等[4]首次将自蔓延高温合成技术应用于切割打孔领域， 使用金属氧化物、 镍粉、 产气剂和铝粉发明了一种用于自蔓延切割的烟火药， 并在之后发明了水下切割炬[5-6]， 使得自蔓延切割装置也可以运用于水下切割. 之后， 1994年George H等[7]沿用了Helms的配方发明了另一款可水下切割的切割炬. 国内自蔓延切割装置的研究始于2004年， 由台州盛世环境工程有限公司开始研制[8-9]. 在此之后， 国内在自蔓延切割的药剂研究[10-12]和装药方式[13-14]研究中获得了大量的成果. 但是， 切割装置结构对于切割效果的影响并没有受到过多的关注[15-16]. 本文主要采用均匀设计法[17-19]和流体力学软件相结合的方式， 通过研究切割装置喷嘴结构参数对切割效果的影响规律， 得到结构参数合理的喷嘴， 从而提高切割效率[20]. 同时， 通过该研究方式可以大幅度减少实验量， 降低实验成本和实验周期.

1 均匀设计方案

自蔓延切割装置由底座， 底火， 药柱， 管壳和喷嘴五部分组成， 图 1(a) 为装置示意图. 其中， 自蔓延切割装置使用锥直型喷嘴， 其结构如图 1(b) 所示， 喷嘴入口与切割器燃烧室相连， 其直径大小受燃烧室直径大小控制， 故不予分析， 根据实际情况取用直径D=23 mm.

图 1 切割装置及喷嘴结构示意图Fig.1 Schematic diagram of the cutting device and nozzle structure

喷嘴入口直径D确定后， 根据锥直型喷嘴结构， 使用出口半径X1(r)， 收缩角X2(α)和圆柱段长度X3(L)3个因素来控制切割装置喷嘴形状. 为研究不同因素水平对切割效果的影响， 对3个因素分别选取8个水平进行计算， 因素水平表如表 1 所示.

表 1 因素水平表

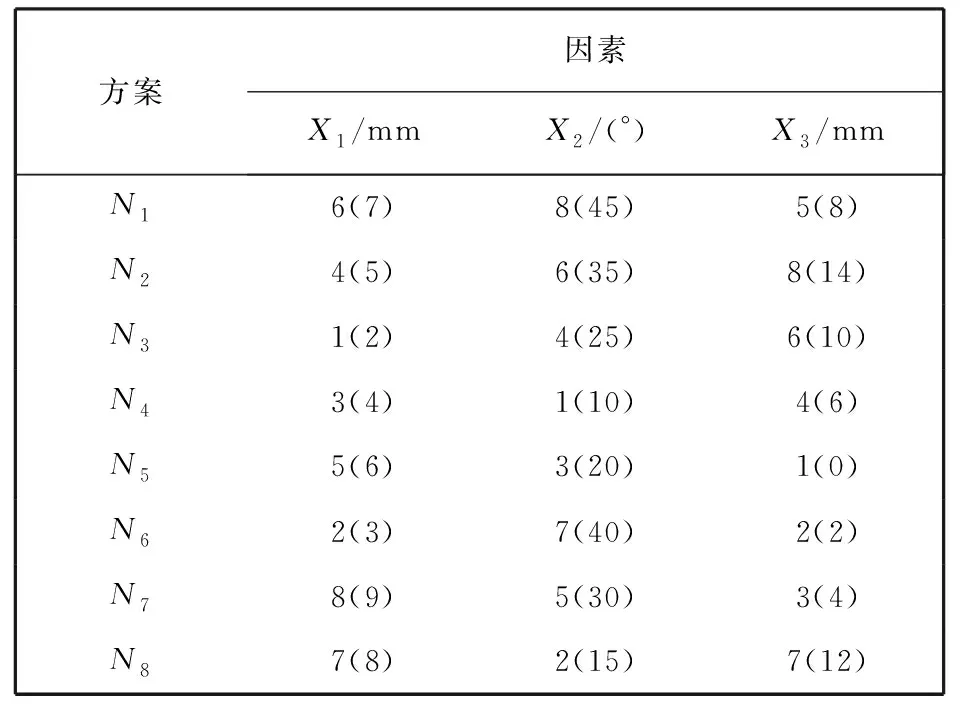
表 2 均匀设计方案

2 模拟计算

2.1 建立喷嘴仿真模型

为研究喷嘴外流场流动特性， 根据流体动力学原理和图 1 中自蔓延切割装置的对称性， 简化模型， 参数如下. 根据表 2 中均匀设计方案对喷嘴和外流场进行二维轴对称模型构建. 由于切割装置燃烧室为直径为23 mm的圆柱管， 因此入口AI长为11.5 mm； 外流场长200 mm， 宽40 mm， 即DE和GF为200 mm，GD和EF为40 mm. 所有模型均采用四边形结构网格处理， 在喷嘴内部靠近出口处进行细化处理， 如图 2 所示.

图 2 外流场模型构建Fig.2 The construction of flow field model

2.2 输入参数计算

本文选用的切割药药剂中含有高热剂， 造气剂， 缓速剂和合金剂4种. 根据最小自由能原理[21]对药剂反应进行计算， 得到切割药药剂反应温度及主要反应产物种类与质量. 其配方组成如表 3 所示， 计算结果如表 4 所示.

表 3 药剂配方

表 4 计算结果

由计算结果可知， 该切割剂配方燃烧后温度达到2 741.9 K， 熔融产物主要由Cu和Al2O3组成， 根据表 5 中产物物理参数计算， 两种熔融物质的体积比Cu∶Al2O3为7∶3.

表 5 产物物理性质[22-23]

由于自蔓延高温合成燃烧速度快， 反应剧烈， 温度非常高， 所以难以精确测量， 因此通过以下公式进行估算[24].

假设燃烧产物全部喷出， 且气体产物为理想气体， 则由质量守恒定律可知

ρsusAs=ρAbr,

(1)

式中：us为出口速度；ρ为切割剂密度；ρs为射流密度；As为出口截面积；Ab为燃烧面积；r为燃烧速度. 实验表明， 当无喷嘴(直径23 mm)时，As≈Ab， 燃速约为2.55 cm/s， 通过表4中计算结果和式(1)计算， 出口速度约为0.8 m/s， 该结果与文献结果近似[25-26].

2.3 设置模拟条件

将建好的模型网格mesh文件依次输入Fluent软件进行计算， 仿真模拟中使用瞬态分析， 打开VOF模型， 能量方程， 标准k-e湍流模型， 运用压力求解器的SIMPLE分离求解算法进行计算. 仿真模拟中入口为AI， 边界条件为Velocity-inlet， 入口速度0.8 m/s； 出口为CD,DE,EF， 边界条件为Outflow； 喷嘴壁面为AB,BC， 使用Wall， 定义为绝热且无滑移； 对称轴为IH,HG,GF， 使用Axisymmetry.

3 结果分析

对表 2 中8种不同尺寸喷嘴进行仿真模拟计算， 选取气体出口速度Y1， 熔融物出口速度Y2和温度损耗程度Y33个结果作为评价喷嘴优劣的条件， 以核心射流区长度Y4作为喷嘴使用参数. 将模拟结果进行统计， 数据结果如表 6 所示.

表 6 仿真模拟结果

3.1 气体出口速度Y1

将各因素水平与气体出口速度进行二次多项式回归分析， 回归结果如表 7 所示. 模型拟合F=27.107 9， 显著性水平为0.002 1<0.05, 相关系数R=0.956 9， 调整后的相关系数为Ra=0.939 0. 回归方程如下

Y1=47.371 428 6-13.104 166 667X1+

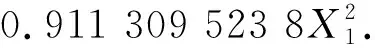
(2)

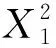
表 7 回归方程的偏相关系数与t, P值

对于自蔓延切割器而言， 气体出口速度越大， 对被切割物的吹力越大， 高速气流可以吹去被切割物体表面熔渣和融化物， 增强其沿厚度方向打孔能力， 因此气体出口速度越大， 切割效果越好. 对二次多项式回归分析结果取最大值， 得到气体出口速度最大值和取该值时各因素的取值如表 8 所示， 当出口半径取值2 mm时， 气体出口速度最大， 为24.808 3 m/s.

表 8 最高指标时各个因素组合

3.2 熔融物出口速度Y2

将模拟结果进行回归分析可得， 熔融物出口速度Y2与各因素间的二次多项式回归方程如下

Y2=45.973 214 3-12.852 976 190X1+

(3)

本次回归分析的相关系数R=0.957 1， 调整后的相关系数为Ra=0.939 5， 总体显著性检验值F=27.308 0， 每个自变量显著性水平均小于0.05， 回归方程显著性水平P值为0.0020<0.05， 此回归方程对结果Y2的拟合效果较好， 回归方程结果如表 9 所示.

表 9 回归方程的偏相关系数与t, P值

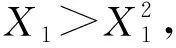
自蔓延切割装置出射物质是经自蔓延高温合成反应生成的多种金属和金属氧化物， 其质量由切割药剂种类和配比决定. 根据动量定义式J=M·V，J为物体所具有的动量，M为物体质量，V为物体速度， 可知， 在质量一定的情况下，V越大J就越大， 射流具有的动能越大， 对被切割材料的冲击效果就越好， 有利于切割打孔. 因此， 对二次多项式回归分析结果取最大值， 得到熔融产物出口速度最大值和取该值时各因素的取值如表 10 所示， 当出口半径取值2 mm时， 熔融物出口速度最大， 为23.879 2 m/s.

表 10 最高指标时各个因素组合

为了验证模拟中两相流速度结果的可靠性， 通过质量守恒定律进行估算， 假设喷嘴壁面光滑， 无附着产物， 则喷嘴入口物质质量等于出口物质质量， 即

u1A1ρ2=u2A2ρ2,

(4)

式中：u1，A1，ρ2分别为入口物质速度， 入口面积， 入口物质密度；u2，A2，ρ2分别为出口物质速度， 出口面积， 出口物质密度. 将数据代入计算可得， 出口速度约为26.45 m/s， 与模拟结果基本一致， 其误差的产生是由于没有考虑物质在喷嘴内的势能和压力的变化、 流动状态等因素. 该结果说明了模拟结果的正确性.

3.3 温度损耗程度Y3

自蔓延切割是依靠切割药剂反应产生的热去融化切割材料实现切割过程的， 在熔融金属射出后， 会发生热量的散失和扩散. 因此， 在熔融金属射出口， 温度损耗程度的多少直接影响到切割的效果. 由模拟结果可知， 在射流稳定后， 温度场也会呈现稳定状态. 受模型大小限制， 温度场无法完全显示， 并且温度场中低温区温度下降快， 会导致读取的数据误差较大， 因此选用钢材融化温度1 800 K作为参考温度， 并引入参数C定义为温度损耗程度：C=R/r， 其中R为射流稳定后外流场中温度曲线(T=1 800 K)距轴线的最大距离， mm；r为出口半径， mm. 实际切割过程中温度耗散程度越小， 能量越集中， 切割效果越好， 切割剂的使用效率越高.

将各因素水平进行二次多项式回归分析， 得出回归方程如下， 相关统计学结果如表 11 所示.

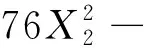
0.002 307 235 272 2X1X2.

(5)

表 11 回归方程的偏相关系数与t, P值

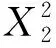
在因素X1限制为2 mm时， 对二次多项式回归分析结果取最小值， 得到温度损耗程度最小值和取该值时各因素的取值如表 12 所示.

表 12 最高指标时各个因素组合

3.4 喷嘴圆柱段长度分析

由射流相关理论[27]分析可知， 圆柱段长度直接影响到了喷嘴外流场的稳定性. 由于喷嘴收缩段的作用， 流体所受压力转变为其动能， 使得流体进入喷嘴的动能不断增大， 射流在进入圆柱段前扰动加剧， 速度方向混乱， 圆柱段可以起到稳定射流状态， 增加射流集中程度的作用. 但实际使用中， 由于圆柱段制作材料摩擦阻力的存在， 圆柱段越长， 射流受到的摩擦阻力越大， 壁面能量损失越大， 出口速度越低， 因此圆柱段长度应当相对较小. 根据式(2)～式(4)分析可知， 喷嘴出口半径取值为 2 mm， 收缩角为16.66° 时其各项指标较优. 从上述回归方程中发现， 当出口速度最大时，X3取值为2.826 4 mm， 当温度耗散程度最小时，X3取值为10.623 1. 综合实际情况和理论分析发现， 圆柱段长度取值2.826 4 mm较为合适.

3.5 切割距离分析

自蔓延切割装置的使用距离是重要的参数之一， 切割装置与被切割材料距离过短会造成出口处压力过大， 引起危险； 如果切割距离过大， 会导致产物热量与能量的大量消耗， 降低切割的效果. 根据湍流自由射流原理[28]， 假设切割药剂反应后产物以均匀的初始速度经喷嘴喷出， 切割时无固定边界对射流限制， 此时可以看作自由射流. 湍流自由射流过程如图 3 所示.

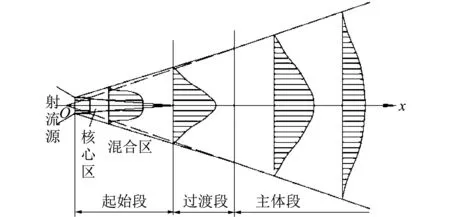
图 3 湍流自由射流Fig.3 Turbulent free jet flow

切割药剂反应后形成产物经喷嘴压缩后形成射流， 射流过程从喷嘴出口开始可依次分为起始段， 过渡段和主体段. 其中起始段内中心部分未与周围流体掺混， 仍保持初始流速的区域称之为射流的势流核心区. 在该区域内由于流速与出口流速一致， 所以在该区域内射流具有的动能最大， 切割效果最好. 因此， 势流核心区的长度决定了切割装置的有效切割距离. 图 4 为各组模拟中轴心线上射流出射距离与其速度的关系， 通过该图可以看出势流核心区之后速度衰减较快， 切割效果将极大削减.

图 4 核心区模拟结果Fig.4 Simulation results of core area

根据表 6 中结果， 将各因素与射流核心区长度Y4进行二次多项式回归分析. 回归方程F值为87.932 7； 经显著性检验， 回归方程显著性水平P为0.000 1， 方程显著. 回归方程拟合相关系数为0.967 5， 调整后相关系数达到0.96 2， 拟合效果较好. 回归方程如下

(6)

表 13 回归方程的偏相关系数与t, P值

将出口半径d=2 mm代入方程， 得出核心射流区长度约为 8.75 mm， 即最佳切割距离为8.75 mm， 该结果符合实验测得切割装置与切割材料使用距离为6～10 mm的实验结果[29-30].

本次模拟结果表明， 当喷嘴出口半径为2 mm， 收缩角为16.66°且圆柱段长度为2.8 mm时， 其两相流体出口速度最大， 温度损耗最小， 切割效果最优， 并且应当使喷嘴与被切割材料保持8.75 mm的使用距离. 文献[31]实验表明， 燃速和密度与模拟条件接近的切割炬使用出口半径为2 mm的喷嘴进行实验， 其出口速度达到25～30 m/s， 最优切割距离为6～10 mm， 并且从射流理论分析了核心射流区长度， 其结果与本文模拟结果相近， 因此认为该模拟结果具有较高的可靠性.

4 结 论

1) 将均匀配方试验法与Fluent流体力学软件相结合， 用于自蔓延切割装置的设计中， 其优点是减少了大量实验次数， 节约时间的同时也节约了实验成本. 结果表明， 该研究方法可以获得较为准确的分析结果， 其结果为切割装置设计提供了数据基础.

2) 运用回归分析法对各评价指标进行分析， 结果表明： 当出口半径为2 mm， 收缩角为 16.66°， 圆柱段长度2.8 mm时， 气体出口流速为24.808 3 m/s， 熔融物出口流速为23.879 2 m/s， 温度损耗程度为1.975 8， 各项切割指标结果最优.

3) 通过分析可知， 当喷嘴选取最优参数时， 切割装置与被切割材料应保持8.75 mm的使用距离. 该数值符合已有实验结论， 证明本次模拟结果与回归分析具有可靠性.