高三复习中学生思维混乱现象的分析与思考

江苏省如皋中学 (邮编：226500)

1 问题的提出——数学思维混乱现象的扫描

题目设方程x+2+2x=0和方程x+2+log2x=0的根分别记为p、q，已知函数f(x)=(x+p)(x+q)+2，则f(0)、f(1)、f(2)的大小关系是______.

在考试中该题的解答状况让笔者非常吃惊．全班共49人，错了30人，与学生交流后，将学生答题错误的现象归纳为以下几种现象.

现象一对求解方程的根的基本方法掌握不全面．部分学生从研究函数g(x)=x+2+2x,h(x)=x+2+log2x入手，求导，作图，求函数零点．事实上，函数g(x)、h(x)的零点从图象角度是无法具体求出的.

现象二对函数的性质理解不深刻．部分学生分别作出y=2x,y=log2x,y=-x-2的图象，但因无法突破y=2x与y=log2x图象的关系，无法发现根的关系.

现象三对图象的对称性认识不到位，一是不能发现函数y=2x与y=log2x图象关于直线y=x对称，二是发现不了二次函数f(x)=(x+p)(x+q)+2对称轴是确定的.

现象四对二次函数的图形和指数、对数函数性质不能灵活运用，无法联系联想．不理解比较三个函数值的大小从图象上看即转化为图象的对称性和函数的单调性.

总之，学生没有认真思考，纵横联系转化的分析习惯，导致在遇到一些有一定综合的问题时思维混乱．

2 问题的阐述——引起学生思维混乱的因素分析

数学思考是指人脑以获取数学知识形成能力、运用知识解决数学问题、激活思维为目的，运用有关的思维方式或方法达到认识数学内容的内在信息处理的过程与活动．数学学习是指获取数学知识和数学活动经验，形成基本技能的认识变化的过程．由此可见导致数学思维混乱的因素有基本概念和基础知识建构不清晰、基本方法积累不完整和思维习惯差等.

2.1 基本概念和基础知识建构不清晰，导致解题方向不明确

日常学习中所遇到的问题，都是由多个数学概念组合而成的，只有从多个角度深刻理解概念的内涵与外延，才能很容易地找到解决问题的思路和方法．由于基本概念不清晰，学生探求不了已知条件转化的途径，不知已知条件可以向哪个方向转化，与所求结论之间有怎样的联系，从而导致思维混乱.

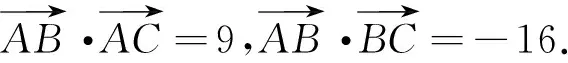
若学生不理解向量数量积的三种表示形式之间可以相互转化，此题就变为难题.

事实上，紧扣向量数量积的三种表示来探求思路如下：

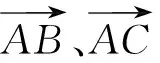
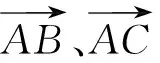
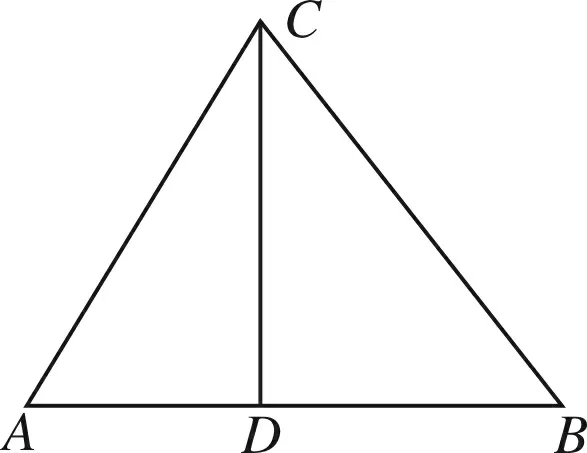
点拨若没有对向量三种语言(符号语言、图象语言、坐标语言)表示的深刻理解和运用向量三种语言的表示意识，学生是无法确定这三个角度解决向量问题的．从向量的基本概念出发，我们常见的思路设计，一是选择恰当的基底，利用向量的符号语言表示向量的数量积、模和夹角等；二是构造图形，探究向量的几何意义，从形出发求解；三是建立恰当的坐标系，转化为坐标语言进行实数运算.

2.2 基本方法积累的不完善，导致解题过程混乱

问题是数学的心脏，而问题解决就是数学思维的核心．问题解决是指主体在数学学习和数学模式识别基础上对数学元素、性质或关系等作出回答或解释的一系列过程，即形成解题的基本方法，如若基本方法积累不全或不完善，会导致解题过程混乱.

例2设集合A={x|x2+4x=0,x∈R}，B={x|x2+2(a+1)x+a2-1=0,x∈R}，若B⊆A，求实数a的取值范围.

学生由B⊆A，得到集合B中的元素都在集合A中，由A={-4,0}，所以-4,0是方程x2+2(a+1)x+a2-1=0的根，得a的值为1或-1或7.事实上，一是依据集合所表示的内容确定集合中的元素；二是依据集合之间的关系确定集合中的元素.

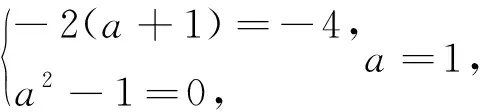
思考二集合A中的元素可以直接确定，但因集合B中的方程x2+2(a+1)x+a2-1=0含参数a，所以确定集合B中的元素较烦，换一个角度来考虑，由B⊆A，依据子集的定义B为∅、{0}、{-4}、{-4,0}，以下分四种情况讨论．当B=∅时，方程x2+2(a+1)x+a2-1=0无解，所以△<0，得a<-1；当B={-4}时，方程x2+2(a+1)x+a2-1=0有两个等根，所以-2(a+1)=-8,a2-1=16无解；当B={0}时，方程x2+2(a+1)x+a2-1=0有两个等根，所以-2(a+1)=0,a2-1=0，解得a=-1；当B={-4,0}时，方程x2+2(a+1)x+a2-1=0有两个根为-4、0，所以-2(a+1)=-4,a2-1=0，a=1，综上a≤-1或a=1.

点拨若没有对研究集合就是要确定集合中的元素基本方法的积累，本题无法获得两种解法的．研究集合，一是要考虑集合所包含的属性，确定集合中的元素是什么；二是依据两个集合之间的关系，确定集合中的元素．确定集合A的元素即求解集合中方程的根，而集合A中方程系数为具体的数，可以直接求方程的根．对于集合B中的方程因含有参数，从两个不同的角度分析：一是从集合B入手，解方程，因为方程的系数含参数，故通过判别式△符号确定分类讨论；二是从B⊆A入手，根据子集的定义，集合A={0,-4}的子集有四个，集合B为∅,{0},{-4},{-4,0}，依次求实数a的取值范围．今后若将一元二次方程变换为一元二次不等式，同样可以从这两个角度将问题分别转化为一元二次方程根的分布问题或一元二次函数的最值问题求解.

问题解决体现在具体的问题中就是将题目中的条件熟练进行转化，这就要我们积累常见的条件转化的基本方法，遇到具体问题时选择恰当合理的方法．基本方法的积累要从最基本问题的解决入手.

2.3 数学思维不具有条理性，导致解题较繁或无功而返

学习数学包含学习数学思考过程和数学思考问题结果，体现在日常教学中，就是解决数学的问题要做到“七分构思”(读题、审题、发散、联想、归纳)，养成思考的条理性；三分表达(书写、运算、订正、反思和回顾)，形成表达、书写的规范性(条理性).

例3等差数列{an}的前n项和为Sn，若Sp=q,Sq=p(p≠q,p、q∈N*)，求Sp+q.

由于思维的习惯比较差，不少学生不善于将已知条件与目标建立一定的联系，不善于观察分析联想，思路混乱，不具有条理性.

思考一利用基本量.

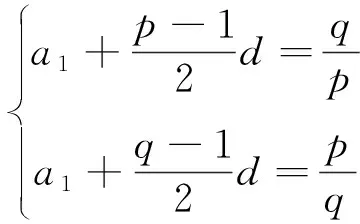
直接求出a1、d.

思考二利用基本量.

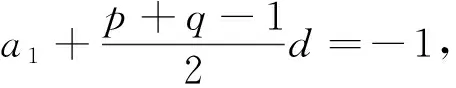
思考三利用性质．因为

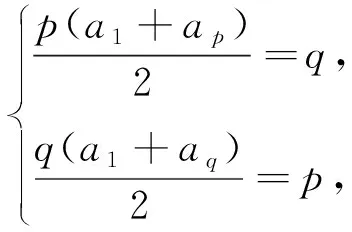
将两式相减求出公差d，利用a1+ap+q=a1+ap+q·d，求得Sp+q；

或者利用Sp+q=a1+a2+…+ap+ap+1+ap+2+…+ap+q-1+ap+q=Sp+a1+pd+a2+pd+…+aq+pd=Sp+Sq+pqd进行转化.

思考四利用图象．点(n,Sn)在Sn=A·n2+B·n上，由Sp=q,Sq=p，求A、B，再求Sp+q.

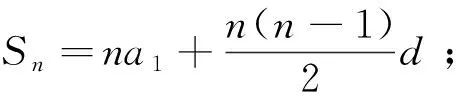
思维条理性体现在学生学习的过程中，即探求解决问题思路的依据是什么，为什么会这么想，探求解决问题的基本途径有哪些，遇到较困难问题时如何迁移与转化.

3 问题的解决——解决学生思维混乱的策略

3.1 从已知条件入手，利用已有的概念和公式将已知条件进行转化

课本的概念、定理和公式是数学思考问题的原点，在思考问题过程中要理解概念的内涵和公式的由来、结构特征及适用条件．遇到一个问题，在审题时要分析已知条件该如何进行转化．转化的依据是什么．对概念的转化要善于依据概念的三种语言(文字、符号、图形)表示，对公式的应用要思考为何选这个公式．这个公式能解决什么问题．公式中的多个量如何进行计算等.

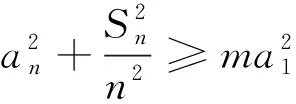
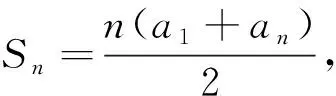
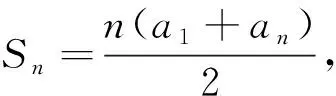
3.2 从结论入手，探寻解决问题的基本方法

遇到已知条件转化的方向不明确时，要善于从结论出发，思考解决这类问题有哪些基本方法，选择哪个方法更优越，教师在讲解问题时要通过追问学生每一步怎么想到这样做的，培养学生善于观察、勤于思考的习惯，促使学生学会如何思考，形成思考问题的条理性.

例5已知数列{an}的前n项和为Sn，an>0，∀m、n∈N*，都有(Sm+n+S1)2=4a2ma2n，求证：{an}为等比数列.

分析∀m、n∈N*,(Sm+n+S1)2=4a2ma2n，依据表达式中m、n的任意性，可对m、n赋值.

思考一

令m=1，得(Sn+1+S1)2=4a2a2n

①

令m=2，得(Sn+2+S1)2=4a4a2n

②

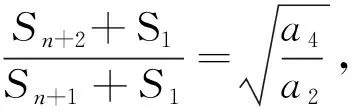
令m=n=1, 则(S2+S1)2=4a22，由an>0，所以S2+S1=2a2=2a1+a2，所以a2=2a1.

在②中再令n=1，(S3+S1)2=4a4a2=(2a1+a2+a3)2，

令m=n=2，S4+S1=2a4，解得a4=4a2，所以a3=2a2，

所以Sn+2+S1=2(Sn+1+S1)，又Sn+1+S1=2(Sn+S1)，所以an+2=2an+1(n≥2)，

n=1、2成立，又a1≠0,数列{an}为等比数列.

思考二令m=n，得S2n+S1=2a2n

③

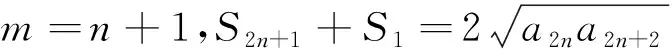
④

在(3)中n→n+1，S2n+2+S1=2a2n+2

⑤

⑥

⑦

⑧

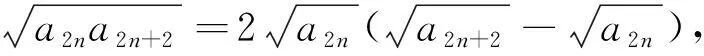
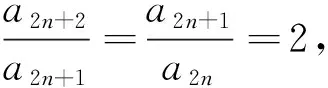
点拨如若从已知来思考，学生都会想到对m、n赋值，对m、n多次赋值，得到多个等式，就不知道如何处理了．若学生没有进行深度思考，在得到多个关系式后难以进行正确的转化，找不到解决问题的方向.

事实上，若从目标出发，要证一个数列为等比数列，依据等比数列的定义，即探求相邻两项的比值为常数.为此，我们要寻求项的关系，而题设中有数列的前n项和与项的关系式，思路一是先消去项，探求和的递推关系式，再转化为项的关系式，在赋值时要将a2m消去，故保留n不变，对m赋值．思路二是消去和Sn、Sm，直接探求项的关系，故先赋值将平方关系式转化为一次，再利用和与项的关系转化为项的递推关系式，此时出现了奇数项与偶数项的关系式，要善于观察下标的结构特征再赋值.

3.3 将已知与目标结合，将问题进行变更

对于所遇到的问题，将问题的已知条件不断地进行变更，即逐步地变换问题的表达形式，使问题从给出的初始状态化归为所要达到的目标状态，直至依据主体所具有的知识不能再表示为其他形式时，考虑从结论出发探求解决问题的方法，若又无法寻求到解决的方法，可通过联想某些模型和结论，采用分析与综合，多途设计，选择某一方向来求解．

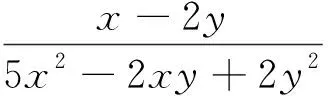
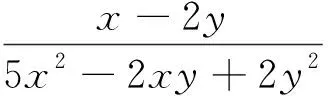
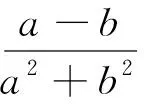
思考二所求式分子为一次，换元令x-2y=t，则x=t+2y，从而将所求式与已知式全部转化为t、y的关系式再求解.

3.4 遇到难题时灵活调整思路，善用猜想、归纳、推理解决问题

数学教学应该是以不断地提出问题，并解决问题的方式来获取新知识、发展思维．教师在高三习题教学中，要科学、合理地创设一系列问题，形成一个螺旋上升的“问题串”，通过“设计问题串”变告知为探索，引导学生探究问题解决的过程，让学生学会设计思考问题的思路．对于遇到的问题用常规思路无法求解时，要依据函数图象、方程的曲线和式、量的几何意义灵活调整思路.

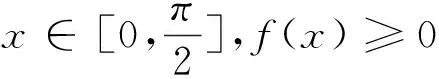
总之，在高三复习中，教师要有意识地培养学生思考问题的条理性，强化基本概念的教学，基本方法的积累，讲解过程中要充分暴露思维过程，让学生弄清楚可以从哪些角度来思考，为什么这样思考，思考的依据是什么，让学生学会思考，形成思考问题的条理性.