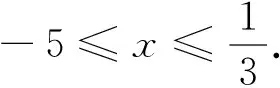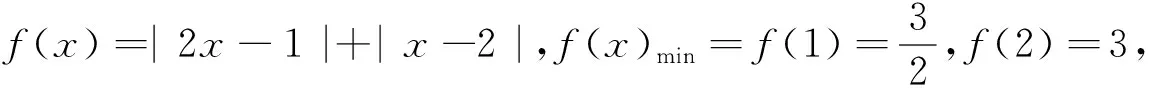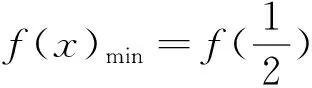速解函数f(x)=|x-a|+k|x-b|(k≠0)的最值问题

贵州省毕节市七星关区北大附属实验学校 (551700) 刘先海

文[1]，[2]中根据，“当k>1时，|x-a|+

k|x-b|=|x-a|+|x-b|+(k-1)|x-b|≥

|a-b|+(k-1)·0=|a-b|，仅当x=b时取等号”，给出了函数f(x)=|x-a|+k|x-b|(k≠0)的最小值求法.本文对其实质作探究，并形成一个针对此问题的快速解法.

文[1]，[2]解法实质是用不等式||a|-

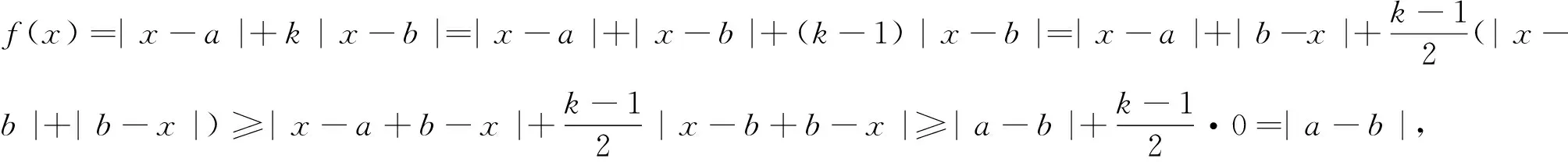
研究发现，函数f(x)=|x-a|+k|x-b|(k≠0)的最值都在两个零点处取得，即f(x)min=min{f(a),f(b)}，f(x)max=max{f(a),f(b)}，根据k的取值范围，有如下结果，

当k>0时，f(x)=|x-a|+k|x-b|(a1时，

f(x)min=f(b)=|a-b|；当0

当k<0时，f(x)=|x-a|+k|x-b|(a

上述结果简单概括为f(x)=|x-a|+k|x-b|(a

例1 求下列函数的最值

(1)f(x)=|x-1|+2|x+2|;(2)f(x)=|x-1|-2|x+2|;(3)f(x)=2|x-1|-|x+2|;(4)f(x)=|x-1|+|x+2|;(5)f(x)=|x-1|-|x+2|;(6)f(x)=3|x-1|+2|x+2|;(7)f(x)=3|x-1|-2|x+2|;(8)f(x)=2|x-1|-

3|x+2|;(9)f(x)=|x-1|+|2x-1|+|3x-1|.

答案：(1)f(x)min=f(-2)=|-2-1|=3；(2)f(x)max=f(-2)=3；(3)f(x)min=f(1)=

例2 (2016年全国高考Ⅲ理24改编)已知函数f(x)=|2x-a|+a．(1)当a=-2时，求不等式f(x)≤|x-1|的解集；(2)设函数g(x)=|2x-1|．当x∈R时，f(x)+g(x)≥3，求a的取值范围．

(2)[f(x)+g(x)]min=(|2x-a|+a+|2x-1|)min=|a-1|+a，∴|a-1|+a≥3，解得a≥2.

例3 (2015年重庆卷)设f(x)=|x+1|+

2|x-a|的最小值为5，则实数a=；

解：f(x)min=f(a)=|a+1|=5，解得a=4或a=-6.

例4 (2017·大同调研)已知函数f(x)=|2x-1|+|x-2a|.(1)当a=1时，求f(x)≤3的解集；(2)当x∈[1,2]时，f(x)≤3恒成立，求实数a的取值范围．

f(x)max=f(2)=3+|2-2a|，由3+|2-2a|≤3得，即|2-2a|≤0，即a=1.