一道动点类竞赛不等式的加强与推广
费红亮 曾善鹏
(1.杭州高级中学 310003;2.杭州电子信息职业学校 310021)
1 结论部分
本文符号约定如下:P是△ABC内任意一点,a,b,c是三角形三边,R表示△ABC外接圆半径,S表示△ABC的面积,P向三边BC,AC,AB作高线分别交边于D,E,F三点,PD,PE,PF分别用r1,r2,r3表示,PA,PB,PC分别用R1,R2,R3表示.
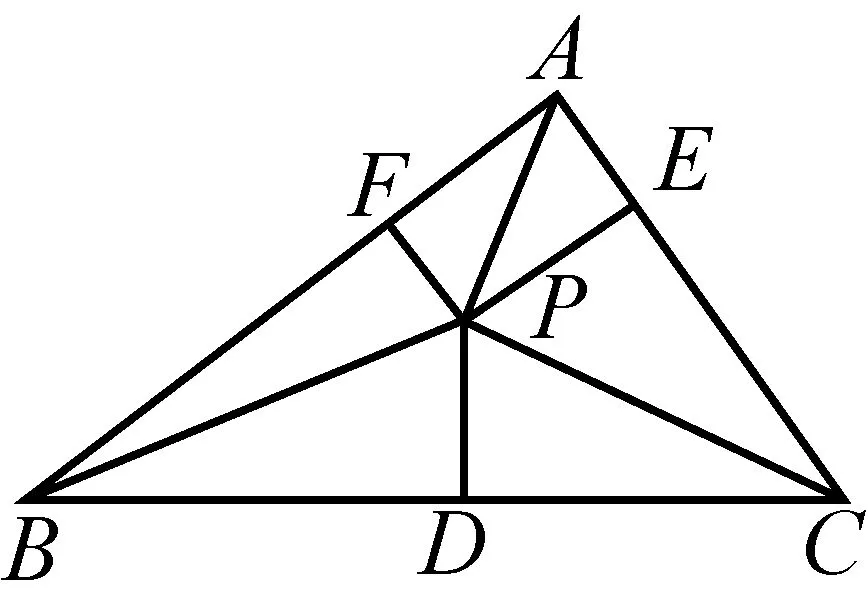
图1
2018年韩国数学竞赛中给出了如下一道几何不等式.
不等式P是△ABC内任意一点,S1,S2,S3分别表示△PBC,△PAC,△PAB的面积,求证:
(1)
首先将不等式(1)进行加强得到:
结论1P是△ABC内任意一点,O为△ABC外接圆圆心,S1,S2,S3分别表示△PBC,△PAC,△PAB的面积,求证:
(2)
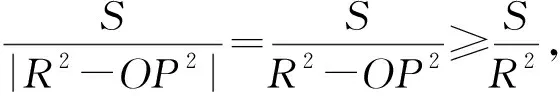
接着将不等式(1)进行n元推广得到:
结论2P是△ABC内任意一点,S1,S2,S3分别表示△PBC,△PAC,△PAB的面积,自然数n≥1,则
(3)
实际上,我们可以得到不等式(1)加强的推广形式,其结论如下:
结论3P是△ABC内任意一点,O为△ABC外接圆圆心,S1,S2,S3分别表示△PBC,△PAC,△PAB的面积,自然数n≥1,则
(4)
注易知结论1和结论2是结论3的推论,因此要证明以上三个结论,只要证明结论3即可.
2 引理部分
引理1(惯性矩不等式)[1]若x,y,z为任意实数,则
(5)
当且仅当x∶y∶z=ar1∶br2∶cr3取到等号.
引理2(Gergonne公式)[2]P是△ABC内任意一点,O为△ABC外接圆圆心,P向三边BC,AC,AB作高线分别交边于D,E,F三点,S,S△DEF分别表示△ABC,△DEF的面积,则
3 证明部分
结论3的证明由引理1知,若取x=ar1,y=br2,z=cr3时,不等式(3)取到等号,即
=(br2×cr3)a2+(cr3×ar1)b2+(ar1×br2)c2.
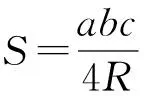
=2R(r2r3a+r3r1b+r1r2c),
所以得到恒等式
(6)
因为PD⊥BC,PE⊥AC,PF⊥AB,
所以有∠A+∠EPF=π,∠B+∠DPF=π,
∠C+∠DPE=π,
结合正弦定理以及三角形面积公式可得
2R(r2r3a+r3r1b+r1r2c)
=2R(2r2r3RsinA+2r3r1RsinB+r1r2RsinC)
=4R2(r2r3sinA+r3r1sinB+r1r2sinC)
=4R2(r2r3sin∠EPF+r3r1sin∠DPF+
r1r2sin∠DPE)
=4R2(2S△EPF+2S△DPF+2S△DPE)
=8R2S△DEF,
所以得到
2R(r2r3a+r3r1b+r1r2c)=8R2S△DEF
(7)
所以由恒等式(6)(7)可得
(8)
因此,由柯西不等式、幂平均不等式、恒等式(8)以及引理2可得
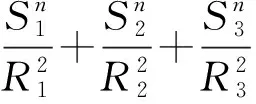
结论3得证.
4 猜想部分
在结论2中,分母的次数是2次,如果将2次换成任意正整数次,结论是否还成立,关于结论2,我们提出了如下猜想.
猜想P是△ABC内任意一点,S1,S2,S3分别表示△PBC,△PAC,△PAB的面积,自然数n≥1,m≥1,则有
——以纽约高线公园的蜕变为例

