几何直观：思维可视化的有效路径

吴静

摘要：几何直观是《义务教育数学课程标准（2011年版）》中提出的十大核心概念之一。几何直观能使数学问题形象化、可视化，有助于发现数量之间的关系，探索解题思路或预测结果。教师要厘清几何直观的内涵，基于学生已有的图形经验和数学问题的特点，通过选图、构图、析图等方面的训练，探寻培养小学生几何直观能力的有效路径。

关键词：几何直观;思维可视化;小学数学教学

中图分类号：G623.5 文献标志码：A 文章编号：1673-9094（2019）12B-0030-04

几何直观是《义务教育数学课程标准（2011年版）》中提出的十大核心概念之一，也是培育数学核心素养的重要内容。借助几何直观能使数学问题变得简明、形象，有助于发现数量之间的关系，增进数学理解，探索解题思路或预测结果。几何直观是思维可视化的有效路径。教学中，教师要引导学生利用几何直观解决数学问题，不断提升学生解决问题的能力。

一、几何直观的内涵和价值

（一）几何直观的内涵

几何直观可以帮助学生直观地理解数学，在推进数学问题的研究、数学发展等方面有着重要的作用。著名数学家徐利治先生指出：“几何直观是借助见到的或想到的几何图形的形象关系产生对数量关系的直接感知。”[1]孔凡哲、史宁中先生把几何直观看作一种数学感知能力，认为：“几何直观是指借助见到的（或想象出来的）几何图形的形象关系，对数学的研究对象（空间形式和数量关系）进行直接感知、整体把握的能力。”[2] 《义务教育数学课程标准（2011年版）》具体阐述了几何直观的过程和意义，明确指出：“几何直观是指利用图形描述和分析问题，借助几何直观可以把复杂的数学问题变得简明、形象，有助于探索解决问题的思路，预测结果。”[3]

综合各家观点，几何直观是为了解决抽象的数学问题，利用几何图形描述和分析问题，以获得对数量关系的直接感知和整体把握的能力。几何直观的本质是思维的直观化、可视化，即将抽象的“数”转换为直观的“形”，通过对“形”的感知和心理操作，获得数学理解，形成解题思路。

几何直观与数形结合是两个不同的概念。从研究的内容而言，数形结合的思想包含着两个方面的内涵：一方面由“数”转化为“形”，直观把握数量关系;另一方面由“形”转化为“数”，利用数的精确性和算法化的优势，探讨、揭示几何图形的特征。几何直观侧重体现由“数”化“形”的内容，主要解决数学问题抽象化的问题。从研究对象而言，几何直观解决的数学问题包括代数问题和几何问题，文字表述的几何问题也是几何直观研究的内容。

（二）几何直观的教学价值

几何直观是借助图形直观感知数学本质、把握数学关系的一种有效方式，是思维可视化的有效途径，有丰富的教学价值。

1.有助于发展数学思考

数学活动的目的是促进学生思维的发展。几何直观通过“图形表征”和“图形分析”增进数学理解，促进对数学问题的思考，从而提升数学思维能力。借助几何直观解题时，不能只停留在对几何图形浅表化的感知，而要深入到数学问题本身进行图形的选择和分析，找到隐蔽的条件和解决问题的线索，建立数量之间的关系，获得对问题深层思考。

2.有助于提升解题能力

几何直观指向数学问题的解决，对于丰富学生的解题策略、提升解题能力有积极的作用。在学生遇到抽象数学问题而止步不前时，几何直观能够有效缩短数学知识的抽象性与学生思维形象性之间的距离，密切沟通“形”与“数”之间的关系，依托“形”直观性、可视化的特点发现隐蔽的数量关系，从而解决抽象的数学问题。

3.有助于培育创新思维

几何直观对于培养学生的创造思维有着重要的意义。一方面，几何直观是对几何图形特征和关系的整体把握，有利于发展学生的直觉思维能力，使学生获得解题灵感，创生新的想法;另一方面，学生在几何直观中的各种差异，为创造性学习提供了机会，使问题思考的方式由“单一”走向“多元”，探索路径从“封闭”走向“开放”。

二、几何直观能力的培养策略与路径

几何直观能力的形成不是一蹴而就的，需要经过长期的实践积累。在日常教学中，教師要积极运用几何直观分析问题，帮助学生形成几何直观的意识，更要通过选图、构图和看图的策略指导，帮助学生积累几何直观经验，培育和发展学生几何直观的能力。

（一）选图——多角度考量，选取恰当的几何图形

几何图形是几何直观的对象，适切的图形能有效促进学生理解数学问题、探明解题思路。教学时，教师要引导学生谨慎选择几何图形表征问题，凸显数学知识的本质。

1.关注图形与学生经验的“匹配度”

几何图形内容十分丰富，包括线、面、体在内的一切形体。受图形学习经验的制约，不同学段的学生对几何图形有着不同的选择取向。学生的图形认知经验是几何直观的基础，只有基于学生已有的图形经验选图，才能发挥几何直观的价值。如，低年级学生处于几何图形的初步感知阶段，适合画集合图和条状图等半抽象的示意图来表示数量和数量关系。中年级学生了解了线、面图形的基本特征，中年级是发展学生几何直观能力的最佳时期，可选线段图和基本平面图形表示问题。高年级学生可以在已有的基础上，适当选用立体图形表征问题。

2.关注图形与数学知识的“契合度”

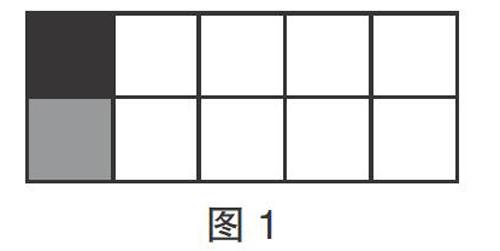
选图表征问题时，教师要考虑与数学知识的“契合度”，直观呈现数学知识的本质，为学生进一步分析和思考问题提供有效的支撑。如，教学除法性质时，教师可选择长方形作为直观载体，帮助学生理解性质背后的原理。以210÷5÷2=210÷（5×2）为例，教师借助图1不仅能帮助学生明了先将210平均分成5分后，再将每一份平均分成2份，就是将210平均分成了（5×2）份，还能基于此图进一步类化，帮助学生建立除法性质的几何模型，使学生获得对性质的一般化理解。

3.关注图形与思维路径的“联结度”

选择的图形要与问题的思考路径一致，能直观启发学生进行数学思考。教师要注意数与运算、探索规律等内容中的图形选择，不仅要选择典型几何模型，还要针对特殊解法选择适合的直观图形，帮助学生克服思维定式，灵活选择方法解题。如，计算1+3+5+7+9+11时，除了借助梯形图将算式转化为（1+11）×6÷2求和，还可以借助正方形图将算式转化为62，简化计算方法。

4.关注图形与表征习惯的“延续度”

图形选择既要考虑图形的多样性和灵活性，还要考虑图形的针对性和普适性。教学时，教师要根据数学知识之间内在的联系选图，用同一类型的图形描述相同性质的问题，帮助学生形成表征习惯。画线段图是表征倍数关系、相差关系以及行程问题等的重要方式，图形题也不例外，可以解决如“一个等腰三角形，顶角是底角的2倍，这个三角形的底角和顶角各是多少度？”等问题。长方形、正方形示意图适用于解决与乘法运算相关的问题，包括解释积的变化规律和乘法结合律等。

（二）构图——多层面切入，用几何图形表征数学问题

在选定合适的几何图形后，根据问题的特点构造图形是培养几何直观能力的关键。教师在平时的教学中要有意识地将内隐的构图策略显性化，帮助学生积累构图经验，掌握构图技巧，进而发展构图能力。

1.丰富构图经验

很多学生无法借助几何图形正确表征数学问题，究其原因是缺乏相应的构图经验。学生的构图经验来源于日常的生活经验和图形的学习经验，两者缺一不可。教师要积极渗透画图技巧，帮助学生获得构图的间接经验，也要及时发现生活经验的不足并增补相关内容。如面对“一个正方形菜地，边长增加3米，面积增加39平方米。原来长方形菜地面积是多少平方米？”时，教师要通过再现实际情境，帮助学生弥补生活经验的缺失，形成正确画图的方法。

2.把握构图要素

为了能使复杂的数学问题变得简明、形象，促进学生的数学理解，教师需要对学生构图进行指导，包括数与形的结合、关键信息的标示以及隐蔽条件的呈示等。一要精准刻画、如实描述题目的有效条件及问题;二要在图上标示出题中的每个数据，特别是解决非图形问题时，要做到“有形必见数”，养成数形结合共同表征问题的习惯;三要关注隐蔽条件的表征，学会将隐蔽的关系外显。如用图表示“一个等腰三角形顶角比底角大20°，求顶角和底角的度数”时，学生要清楚标出“三角形内角和180度”这个隐藏着的信息。

3.明晰构图顺序

构图过程实际上是梳理题目信息，再次明确题意的过程。构图的顺序能反映学生的思维状态和水平。通常，构图能力较差的学生只关注“细节描画”而忽略“整体构造”，按部就班表征问题信息，导致陷入“只见树木不见森林”的迷局。教学中，教师要引导学生按先“整体”再“局部”的顺序构图，建立各个数量之间的层级关系。如用长方形描述“一个长方形操场长100米、宽80米，长增加3米，宽增加2米，面积增加了多少平方米？”等问题时，学生要先明确长、宽变化后仍然是一个长方形，再根据长、宽的增减变化确定变化后长方形的长和宽，最后再勾画出整个图形。同理，用线段图描述“行程问题”时，学生要在明确对象运动时间、地点和方向的情况下，着重表征行走的路程，确立路程和距离之间的关系。

4.变换构图方式

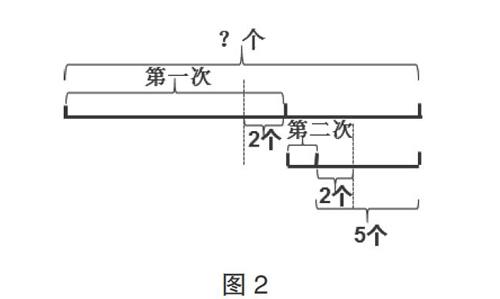
不同的构图方式在启迪学生思维方面有着不同的价值。在学生无法借助几何图形直观理解数量关系时，教师要突破常规思路的限制，根据题目特点灵活调整构图方式，帮助学生理清关系。如教学“一筐梨，小红第一次吃了一半多2个，第二次吃了剩下的一半少2个，最后剩下5个，原来一筐梨有多少个？”，由于题目中的信息多、关系复杂，仅用一条线段表征问题中所有的信息，很难发现数量之间的关系。如果换成多条线段表征信息（如图2 ），并将“一半”、每次“拿走”的信息用长虚线、大括号凸显，就能使关系明朗化，帮助学生顺利解题。

（三）析图——多路径探索，借图形关系把握数量关系

“并非画出几何图形就可以称为借助几何直观，而是需要借助几何图形发现所研究图形的本质、关系或规律。”[4]几何直观不仅要借助图形表征数学问题，还要利用对图形的观察和分析，寻求解决问题的思路和方法，直至获得结论。教学中，教师要引导学生利用几何直觉，结合图形特征运用图形变换和几何推理等方式，帮助学生获得看图分析问题的能力。

1.利用几何直觉探明方向

借助于几何图形的形象直接感知数学研究对象，能获得对数量关系的直观感知和直觉判断，以及对结果的预测。教师要重視几何直觉在直观中的作用，鼓励学生根据现有的图形信息大胆猜测数量关系，把握研究方向并预测结果。如教学圆面积时，教师可在学生明确圆面积和圆的半径r有关的基础上，出示边长为r的正方形，让学生猜测圆面积和正方形面积之间的关系，以此确定圆面积的范围在2r2～4r2之间，再以此为研究起点将圆无限等分后转化成近似长方形，推导出圆面积计算公式。

2.根据图形特征探寻关系

几何图形具有过程和概念的意义，更利于学生探索解题思路。在借助几何直观解决问题时，教师不仅要确认学生对图形特征有准确、清晰的认知，还要引导学生基于已有图形信息，根据图形特征进行联想和推测，发现隐蔽的数量关系，获得解决问题的线索。在图形教学时，教师就要有意识地让学生根据图形特征联想关系。如，在认识圆时，教师就可以让学生进行“根据给出的数据，你还想到了什么”的信息联想训练（如图3 ），沟通长方形长、宽与圆的半径、直径之间的关系以及正方形边长和圆的直径之间的关系，为看图分析并解决稍复杂的圆的实际问题积累思维经验。

3.结合图形运动探索思路

利用图形的运动进行图形转化，常常能“化腐朽为神奇”，瞬间使复杂的数学关系变得简单明了。教师要引导学生用运动的眼光看待数学问题，发现更加简单、有效的解题路径，发展空间想象力。如，解决“一块长方形菜地，长和宽都增加3米后，面积增加69平方米，原来长方形菜地的周长是多少米？”（见图4 ），在用长方形示意图描述问题，将增加部分面积分成3个部分后，学生就需要借助图形的旋转，将①部分旋转至②部分的右侧，与②部分拼成一个宽为3米的大长方形，先求出长方形的长（原长方形的长与宽的和），进一步求出原长方形的周长。在解决立体图形问题时，学生也需要通过图形的运动，将三维立体图形问题转化成二维平面图问题，从而找到解决问题的最优策略。

借助幾何图形“看”出数量关系是一种智慧，更是一种能力。教师要加强几何直观的策略指导，让学生掌握用图表征问题的一些基本技巧，获得画图的基本技能;还要通过创设适当的问题情境，帮助学生主动产生几何直观的意识;更要提供利用几何直观表达和交流数学问题的机会，让学生在尝试开展图形表征、分析的过程中，在对比辨析中，不断提升几何直观水平。

参考文献：

[1]徐利治.谈谈我的一些数学治学经验[J].数学通报， 2000（5）：2.

[2]孔凡哲，史宁中.关于几何直观的含义与表现形式——对《义务教育数学课程标准（2011年版）》的一点认识[J].课程·教材·教法， 2012（7）：93.

[3]中华人民共和国教育部.义务教育数学课程标准（2011年版）[M].北京：北京师范大学出版社， 2012：6.

[4]史宁中.例说小学数学中的几何直观[J].小学数学， 2017（10下）：4.

责任编辑：石萍

Geometric Intuition： An Effective Way of Thinking Visualization

WU Jing

（Jiangyin Chengjiang Central Primary School， Jiangyin 214400，China）

Abstract：  Geometric intuition is one of ten core concepts proposed by Mathematics Curriculum Criterion in Compulsory Education （2011 version）， which can make mathematic problems concrete and visualized， helping students discover the relationships between quantities， explore solutions and anticipate results. Teachers should clarify the connotations of geometric intuition and train students ability of selecting， structuring and analyzing graphs on the basis of students previous  experience and the features of mathematic problems， trying to find the effective ways of cultivating students competence of geometric intuition.

Key words： geometric intuition; thinking visualization; primary school mathematics teaching