拉长活动体验 让数学思维悄然发生——以《立体图形的复习拓展》为例

江苏海门市证大小学 张玉华

教学目标：

1.使学生在操作活动中进一步认识长方体、正方体、圆柱、圆锥等立体图形的特征，经历探索立体图形表面积、体积有关知识的过程，并能运用知识解决实际问题。

2.使学生在活动探索中进一步体会知识之间的内在联系，培养观察、比较和归纳整理的能力，发展空间观念，增强立体思维。

3.使学生在活动思考中进一步感受数学知识、方法之间的内在联系，体验与同学合作交流以及获取知识的乐趣，增进对数学学习的积极情感。

教学重难点：

重点：打通立体图形和平面图形之间的联系，形成完整的知识结构。

难点：发展学生的动手操作能力和空间观念。

原有经验：学生已经认识了长方体和正方体、圆柱和圆锥，知道它们各自的特征，并能进行表面积、体积的相关计算。

一、动手操作，自由创造

师：小学阶段，我们学习了哪些立体图形？其实平面图形和立体图形的关系非常密切，这节课我们一起“玩转”立体图形。

师：如果给你一张长方形纸，你能创造哪些立体图形？

出示活动单：（1）用提供的长方形纸创造立体图形。（2）组内交流创造方法，说说长方形和立体图形的联系。

生多样化地创造立体图形，在小组里交流探讨，碰撞创造的火花。

数学活动的本质在于：必须要有高层次思维的参与，要以具体的问题为载体，以自主合作探究为途径，聚焦数学思维的发展。在活动单的指引下，相信学生实践的能力和思考的力量，能生成不一样的数学教学资源。

二、深入思考，互动生成

师根据学生的不同创造分类呈现方法：

1.卷一卷的方法

动手操作是解决问题的有效途径，但是动手操作后静下心来思考才会让学习真正发生。

师借助学生的实践感悟，随机出示具体的数学问题：

①如果长方形纸的长是12.56厘米，宽是9.42厘米，卷成的圆柱高是多少？

②如果为这两个圆柱配个底面，该如何配？

上面两个问题简洁、明确，有一定的思维容量。具有应用性功能的问题便于学生对问题中所包含的显性或隐性的信息主动加以构造，激发学生对数学本质的识别，从而进行有价值的数学思考。

2.折一折的方法

学生想到了沿着长对折再对折，折成了一个长方体；沿着宽对折两次也能折成一个长方体。那么，如何从操作的层面进入深一层次的内化，帮助学生从感官层面的感受提升到理性层面的理解呢？

师提出了以下两个问题：

①长方形和折成的立体图形有哪些相通点？

②两个长方体哪个表面积大？

学生展开了热烈的讨论，很快他们有了发现：两个长方体的侧面积一样，因为它们都是用同样的长方形折成的；长或宽的1/4是底面正方形的边长，通过推算，学生验证出沿着长折成的长方体的表面积大。

教师相信学生的学习潜能，提供给学生自主、开放、富有挑战性的空间，学生的思维就可以自由驰骋、心灵自由发展，从而获得数学核心素养的熏陶和提升，数学学习便有了宽度。这时，学生的探究热情一点也不减，教师又一次巧妙组织学生深度学习：

师：你们折成的长方体比较特殊，知道特殊在哪儿吗？

生：（若有所思）长方体的底面是正方形。

师：那你们能用这张纸折一个普通的长方体吗？

生（交流）纷纷认为普通的长方体底面是长方形。

师巡视中发现学生在折的时候遇到了麻烦，不能一下子折成底面是长方形的长方体。

师找到由失败到成功的学生，展示并介绍折的经验。

生频频点头、感同身受、若有所悟、豁然开朗。

在学生代表的经验介绍中，其余学生打开了思维大门，他们在一层层“讲理”的过程中不仅知道了“是什么”，而且知道了“为什么”，进而探索出数学的内在规律，学生思维最大限度地向纵深方向发展。

师：（出示几种不同的折法）判断哪个可以折成普通长方体？联系长方体特征说说为什么？

生辨析中明确要使长方体底面是长方形，根据其特征，相对的面需要完全相同。而不同的长方形只要保证三条折线中间线不动，另两条等距离移动便可。

师：能用这张纸折成正方体吗？

生：不能。

师：怎样的长方形纸可以折成正方体？

生：长是宽的4倍。

借助学生已有经验，让学生从不同角度探寻属于自己的认知路径，对所学内容做横向延伸，最终实现对数学知识的主动构建。这里催生的新问题，能够聚合学生的知识和方法储备，支撑起对知识内核的深层次研究，学生的思维获得了拓展、智慧受到了启迪、学习力得到了提升。

3.转一转的方法

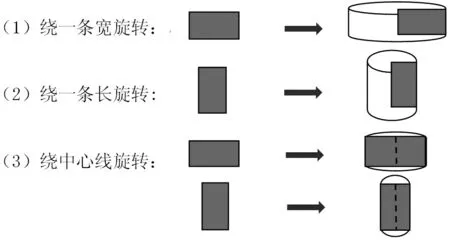
旋转长方形，学生玩得不亦乐乎，伴随着玩转的过程，学生能非常清晰地说出转出的圆柱的半径、直径、高，熟练地计算出这些圆柱的侧面积、表面积、体积，而且总结出了“矮胖子”体积大的结论。这是一个有温度的数学活动方式，站在学生的立场，从学习者的角度出发，让学生伴随着积极的情感体验经历活动的过程，产生持久的学习兴趣，并逐步转化为学习的意志。

4.移一移的方法

既然有图形的旋转，便自然想到了图形的平移。当教师提出还能怎样创造立体图形时，学生脱口而出，可以平移平面图形，平移留下的痕迹也是立体图形。

生：相同图形叠在一起也能创造出立体图形。

师：是的，这都被你想到了，真厉害！生活中有这样的例子吗？

生：相同的书叠放在一起；相同的硬币叠放在一起……

三、心脑合一，拓展延伸

师：除了可以直着叠，也可以斜着叠，还可以参差着叠……

出示阅读材料“祖暅原理”，借助图形简要介绍。

生多种感官协调促感悟。

师：如果把长方形纸的一条边分成三等份可折成三棱柱，分成四等份可折成长方体，分成五等份、六等份……这样不停地往下折，就形成了什么？

生：圆柱。极限思想悄然生成，数学思维不断提升……

四、教学反思

数学活动经验的积累是提高学生数学素养的重要标志。帮助学生积累数学活动经验是数学教学的重要目标，是学生不断经历、体验各种数学活动过程的结果。在活动中学生可以感悟“眼睛看不到的心可以到达”，从而帮助学生从感官层面的感受提升到理性层面的理解，有利于他们对知识表象加工并重新组合，达到对知识本质的理性思考。

长方形纸卷一卷后把长边对接可以形成一个圆柱，沿着宽对接形成另一个圆柱，在互动交流中学生关注到两个圆柱的侧面积相等且都是这一张长方形纸面积，为两个圆柱配上了合适的底面；长方形纸折一折可以折成不同的长方体，有长或宽的1/4的正方形面作底面的特殊长方体，也有一般的长方体，根据长方体相对的面完全相同这个特征，在层层辨析中学生探索出只要保证三条折线的中间线不动，另两条等距离移动便可根据折痕围成长方体；长方形纸可以沿着长边旋转，也可以沿着宽边旋转，还可以沿着长边和宽边的中轴线旋转，旋转的痕迹形成圆柱。学生找准了圆柱和原来长方形之间的关系，找到了圆柱的半径、高，算出了圆柱的侧面积、表面积和体积。长方形纸来回等距离移一移，移动的痕迹也是长方体，由这种方法学生还联想到了用层叠物体的方式组成长方体、圆柱、三棱柱等，这样“祖暅原理”就油然而生。一张纸卷一卷、折一折、转一转、移一移，玩出了不一样的效果，数学活动不仅能丰富学生数学学习的过程经历，还可以深化其对知识的结构性理解，凝聚着学生的情感期待。

本节课从“面”到“体”的空间转换中，学生的思维有了一次大跨越，从最初想到卷的方法到折的探索再到用纸快速旋转、快速移动层叠出立体图形的整个探索过程，学生不仅要依附动手操作，还需要动脑思索、用心延伸。把握知识本质，寻找几何形体间的联系，以“显”促“隐”，指引学生向深度、广度思考，整个过程拉长了数学活动体验、注重了知识的“生长点”与“延伸点”，灵活运用知识的结构和体系、正确处理局部知识与整体知识的关系，从而引导学生思维品质悄然生成。♪