一类发散级数阶的估计

彭建华，杜 燕，范崇秀

（重庆理工大学 数学与统计学院，重庆 400054）

发散级数在数学史上具有重要地位，它与微积分的发展密不可分，被广泛应用于数学研究以及物理等其他学科中［1-2］。发散级数在函数表示或者计算中有着重要的意义。本文利用文献［3-5］中阶的估计方法，对一类发散级数的阶进行了估计。

定理1设bn ＞0，且an ＝o（bn），n→∞。则有

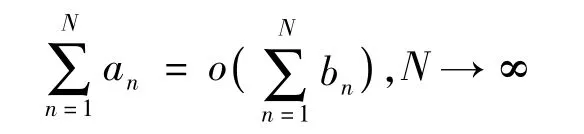
证明由假设知，对任意ε＞0，存在M＞0，当n＞M时，恒有

因此，对任意N＞M，有

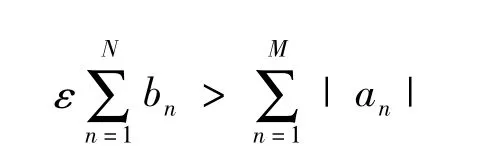
Stolz定理在数学分析中用来证明或者计算某种类型极限时是很有用的一个定理，但在文献［6-7］等数学分析书上关于该定理的证明都非常复杂，下面利用定理1，给出一个简单的证明方法。

例1（Stolz定理）设数列｛yn｝单调递增，yn→∞，n→∞则

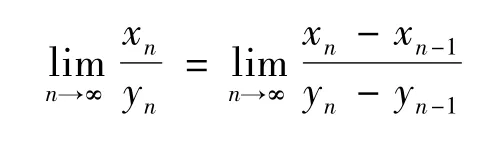
此处假定右端的极限存在。

证明设则

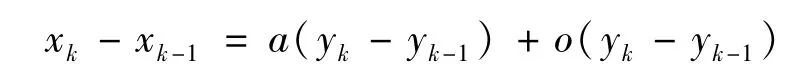
对k求和，得

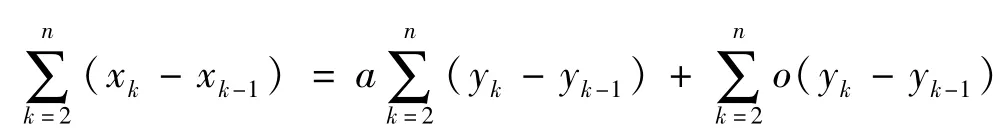
由于yn＋1＞yn，yn→∞，所以，由定理1可得

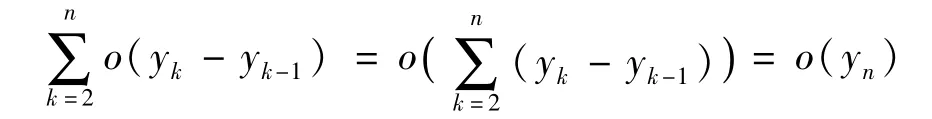
由此得到xn-x1＝a（yn-y1）＋o（yn）。将上式同除以yn，可得

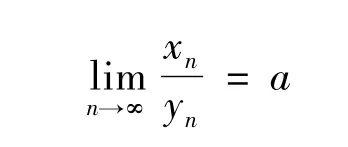
如果a＝＋∞，则可以推得数列｛xn｝单调递增，且xn→∞，n→∞，由已证得的结论得如果a＝-∞，推导过程类似。

定理2设（bn ＞0）在区间［0，1）收敛。又1-），且an ＝o（bn）（n→∞），则 有f（x）＝o（g（x）），x→1-。

证明由假设知，对任给的ε＞0，存在N，当n＞N时，有｜an｜＜εbn，所以当0≤x＜1时，有

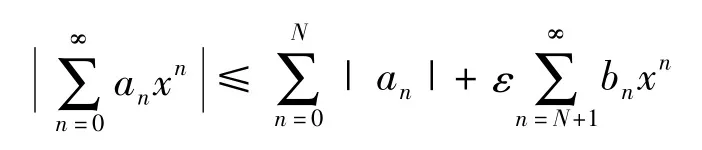
由于g（x）→∞（x→1），所以存在δ＞0，当1-δ＜x＜1时，有

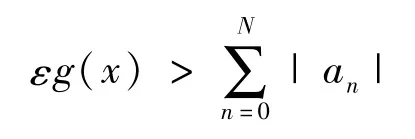
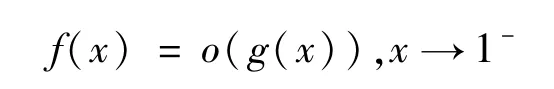
定理3设（bn ＞0）在区间［0，1）收敛。又1-），且an ～bn（n→∞），则f（x）～g（x）（x→1）。

定理4设级数f（x）和g（x）＝在区间［0，1）内收敛，令

且满足条件

1）tn＞0；

3）sn＝o（tn），n→∞；

则有f（x）＝o（g（x）），x→1。

证明由幂级数乘法定理，得

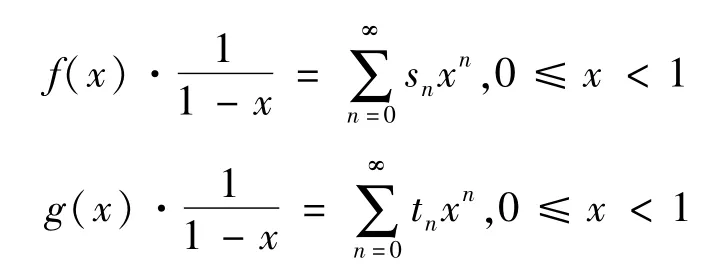
由假设条件及定理2，得

定理5若定理4中的条件（3）换成sn～tn，则有f（x）～g（x），x→1。

例2证明：

证明由于，所以

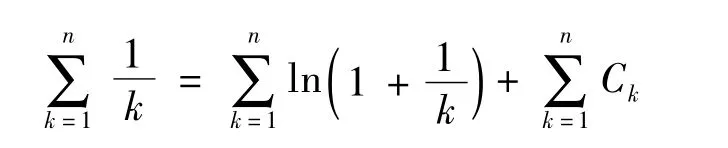
这里γ是一常数，因此证明了n→∞。

例3 设an～lnn，n→∞，则

证明因为

例4 证明lnΓ（n）这里C为一常数。

证明 由于lnΓ（n）＝ln（（n-1）！）＝而

这里C为常数。