PMSM 中基于改进BFO算法的无传感器速度控制方案

孙汉卿，张世杰，王桂芝，连卫民

（1.河南牧业经济学院 信息工程学院，郑州 450001；2.河南工业大学 电气工程学院，郑州 450001）

永磁同步电机（permanentmagnet synchronous motor，PMSM）［1］常用的控制系统有转子磁场定向控制（FOC）［2］和直接转矩控制（DTC）［3］。这些系统都是根据速度控制器输出速度信号来调节磁通和转矩，故速度控制是整个系统的基础。目前，常用的非线性速度控制方法为比例积分（proportion integration，PI）控制器［4］。然而，传统PI控制器的控制参数需要人工设定，且不会随着环境变化而自适应改变，不能满足对环境的鲁棒性要求［5］。为此，有学者将一些自适应机制融入PI控制器中，例如模糊PI参数自整定控制器［6］，基于遗传算法［7］、粒子群优化［8］等进化算法的PI参数自整定控制器等。

另外，对时变、非线性控制系统的控制，传统PI控制器性能不是很好。增强PI控制器性能的较好方法是使用分数阶控制器［9］。分数阶PI控制器PIa中，通常I的阶数为分数阶［10］。因此，除设置KP、KI外，还需设置积分的分数阶a。

基于上述分析，本文利用分数阶PI控制器代替PMSM中的PI速度控制器。通过融入粒子群优化算法中的信息共享机制和自适应步长来改进细菌觅食优化（bacteria foraging optimization，BFO）算法，形成改进型细菌觅食优化（improved BFO，IBFO）算法，并利用IBFO算法来优化KP、KI和a参数，以获得最佳的控制器。另外，在适应度函数中考虑了转速控制的时间绝对误差积分（integrated time absolute error，ITAE）和超调量，有利于提高控制稳定性。通过实验与传统PI控制器和传统BFO算法优化参数的PI控制器进行比较，结果证明了所提出控制方法具有优越性能。

1 PMSM 数学及控制模型

1.1 PM SM 数学模型

PMSM结构中分为2个轴，分别为d轴和q轴，这2个轴的气隙长度和电感都不同。d轴定义为励磁绕组的磁通产生方向［11］，q轴与d轴成90°。PMSM结构如图1描述。

图1 PMSM的结构

PMSM模型可以通过转子旋转坐标系（d-q轴）建模为1个电路，如图2所示。根据电路电流和电压关系式，d轴和q轴的定子电压分别为：

式中：vd、id表示d轴的电压和电流，iq、vq表示q轴电压和电流；λd和λq分别表示2个轴的磁链，可通过定子电流、电感和恒定磁链λm来计算获得，如式（3）（4）所示；ωe表示电机转速，rs表示定子电阻。

式中：Ld、Lq分别为d-q轴电感。将式（3）（4）代入式（1）（2）中，定子电压方程可修改为：

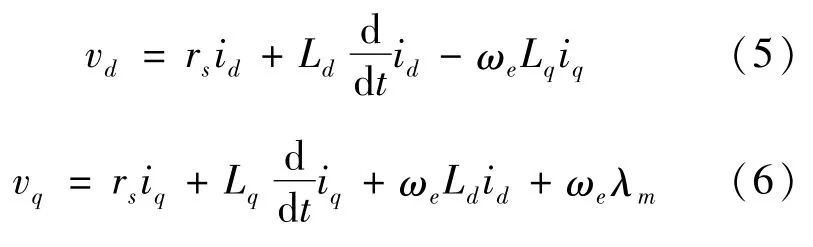
电磁转矩Te为：

式中：Tl为负载转矩；P表示电机极数；B为阻尼系数；J为惯性矩。

图2 PMSM的等效电路

1.2 PMSM 无传感器控制模型

本文中，选择磁场定向控制（FOC）方式来控制电极，其系统框图如图3所示，其主要由5个模块组成，分别为速度控制器、电流控制器、逆变器、PWM发生器和位置估计器［12］。

图3 PMSM的磁场定向控制系统框图

1.2.1 FOC控制模型

磁场定向控制的主要思想是将定子电流矢量加在q轴上，把转子磁通加在d轴上，这意味着id（ref）＝0。为此，电磁转矩可修改为

式中：Kt为电机转矩系数。那么，在状态空间中，PMSM方程可建模如下：

1.2.2 基于EKF的速度估计

在FOC无位置传感器的控制系统中，电机的当前速度是通过一些转速估计算法，根据电机电流、电压等信号进行估计，然后将其作为实际转速反馈到PI控制器中，如图3所示。为此，速度估计的准确性直接影响电机速度控制器的性能。本文将电机三相电流信息变换到αβ轴（两相静止坐标系），然后采用基于扩展卡尔曼滤波器（EKF）来估计电机转速。

卡尔曼滤波器（KF）是一种递归算法，其使用一种多输入-输出系统的随机状态空间模型和噪声统计来获得系统状态变量的最优估计。本文假设系统中的过程噪声和测量噪声均为零均值的高斯白噪声。通过最小化估计误差的协方差来获得最优的状态估计。EKF可以实现非线性系统的近似线性化，提高求解精度。PMSM 模型的离散化可表示如下：

式中：xe（k）为k时刻所估计的状态向量，即xe＝（isα，isβ，λrα，λrβ，ωr，TL）T；z（k）为k时刻的观测向量，即为状态向量与输入之间的非线性函数；ue为输入向量；He为观测矩阵；G为噪声加权矩阵；v（t）为测量噪声。

如上所述，EKF将PMSM的离散化非线性模型进行线性化，并在线性化中对状态变量进行估计，表示为

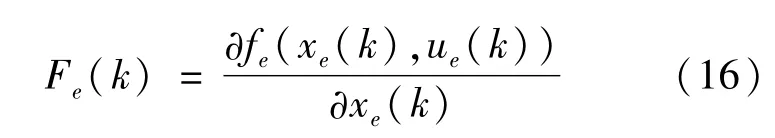
2 分数阶PI速度控制器

在PMSM的磁场定向控制系统中，速度控制器是整个系统的核心部分，其决定着后续转矩和励磁的控制性能。通常速度控制器采用传统PI控制，但其性能有限，且参数不能自适应调整。近年来，越来越多的研究人员在控制领域使用分数阶微积分控制，分数阶微积分是处理分数幂微分或积分算子的一种技术［12］。若设定ωref为电机的参考速度，ωact为驱动器的实际输出速度，那么在时域中的分数阶PI控制器PIa的表现形式为

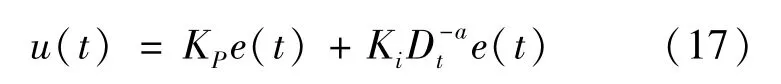
控制器的输入e（t）为速度差，表示为

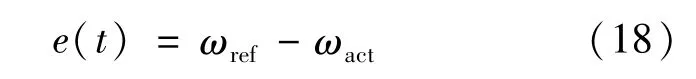
式中：为分数微分算子，表示函数f（t）的a阶导数，定义如下：

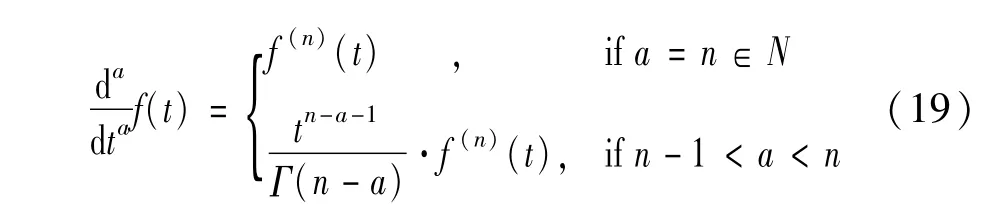
分数阶PI控制器的传递函数在频域上表示为

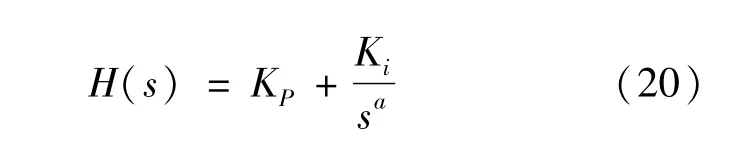
式中：KP和Ki为分数阶PI控制器的比例和积分增益值；a为分数积分器的非整数阶。

对于分数阶PI控制器的设计，参数KP、Ki和a决定了其上升时间（tr）、稳定时间（ts）、峰值超调百分比（po%）和稳态误差（ess）。因此，要获得良好的瞬态响应，需要获得合适的控制器参数组合。由于这些参数组合的解空间较大，人工调节效率较低，所以通常采用智能优化算法来寻找最优参数组合。

3 基于IBFO的速度控制器参数优化

3.1 参数优化系统架构

本文将分数阶PI速度控制器中的3个参数KP、Ki和a作为优化对象。提出一种改进型BFO算法（IBFO），基于速度差信息来优化控制器参数，以此来提高速度控制的准确性。基于IBFO的速度控制器的系统框架如图4所示。

图4 PI速度控制器参数优化框架

通常，PI控制器参数优化的目标函数为转速控制的时间绝对误差积分（ITAE）［13］，表示为

为综合考虑速度超调情况，本文在目标函数中融入了超调量σ，σ由速度峰值与参考速度的比值来计算。这样有利于PI控制器产生更小的超调量和振荡。那么，最终的目标函数O的表达式为

式中：w为权重因子，用来权衡ITAE与超调量的比重。这里，由于ITAE反映速度控制的稳定性，相对而言比超调量更为重要，所以本文设置w为0.3。另外，目标函数值越大说明该参数组合下控制器的性能越低。

3.2 传统细菌觅食优化算法（BFO）

BFO是由人类大肠中“大肠杆菌”觅食行为而启发的一种新型智能优化方法。在这种觅食理论中，细菌以单位时间内摄入能量最小化的方式来搜索并获得营养物质，细菌会通过趋化性行为聚集到营养丰富的区域。BFO算法中细菌觅食步骤主要分为3个部分，分别为趋向性操作、繁殖操作和迁徙操作［14］。

趋向性操作：趋向性操作中包含2个基本操作，即旋转和游动［15］，细菌在觅食过程中通过这些操作逐步移动到食物源处。游动操作是细菌根据上一步的方向进行游动。而旋转操作中，细菌会根据当前方向上位置和上一步位置的适应值旋转方向，朝其他随机方向游动。

繁殖操作：细菌繁殖过程中，根据细菌的适应度，淘汰一些寻优能力较弱的细菌，并复制相应数量的较优细菌进行替换。繁殖过程中产生的较优细菌副本具有与本体相同的属性。

迁徙操作：菌群经过若干代繁殖后，将以给定概率执行迁徙操作，移动到新的寻优空间，以此使细菌进行全局寻优，避免陷入局部最优。

通常，细菌i在经过第j轮趋向性行为、第k轮繁殖行为和第l轮迁徙行为后的位置用θi（j，k，l）来表示。

3.3 提出的改进型BFO算法（IBFO）

在传统BFO算法中随机生成旋转操作的方向，随机方向会导致收敛到全局最优解的速度变慢。在IBFO算法中，利用了PSO具有良好的社会信息交换能力，使旋转行为中的方向根据全局最佳位置和每个细菌的个体最佳位置来决定，而不是随机确定。在趋化循环中，游动方向的更新公式为

式中：φ（j）表示细菌在第j次趋向性操作中的方向；pbest为每个细菌的个体最佳位置；gbest为菌群的全局最佳位置；C1、C2为学习因子，通常设置为2；wφ为惯性权重，决定对上一个方向的继承程度。IBFO算法的流程和具体步骤见图5所示。

步骤1初始化参数：p、S、Nc、Ns、Nre、Ned、Ped、C（i）（i＝1，2，3，…，S）、θi。其中：p为搜索空间的维度；S为细菌总数；Nc为趋化操作的代数；Ns为最大游动代数，Nc＞Ns；Nre为繁殖操作的代数；Ned为迁徙操作的代数；Ped为迁徙的概率；θi为第i个细菌的位置；C（i）为旋转方向的步长大小。初始化种群，生成随机向量φ（j），其取值范围为［-1，1］。

图5 提出的IBFO算法的流程

步骤2迁徙循环：l＝l＋1。

步骤3繁殖循环：k＝k＋1。

步骤4趋向性循环：j＝j＋1。

对于每个细菌i（i＝1，2，3，…，S）：

1）计算细菌i的适应度函数O（i，j，k，l）；

2）令当前最佳适应度Olast＝O（i，j，k，l）；

3）旋转操作：计算旋转方向

4）根据以下策略移动到新位置：

5）重新计算O（i，j，k，l）；

6）游动操作：

①设置游动代数m＝0，计数游动代数；

②当m＜Ns（即没有达到最大代数）

· 令m＝m＋1。

· 若适应度O（i，j，k，l）＜Olast（即获得更好的适应度）。

· 令Olast＝O（i，j，k，l），并移动到该位置θi（j＋1，k，l）＝θi（j，k，l）＋C（i）φ（j），计算新位置θi（j＋1，k，l）的适应度函数值。

· 否则，令m＝Ns，循环结束。

7）如果i＜S，转到下一个细菌（i＋1）（即返回步骤4的1）去处理下一个细菌）。

步骤5如果j＜Nc，转步骤4，继续趋化循环，因为细菌的生命没有结束。

步骤6繁殖操作：

1）对于给定的k、l，计算每个细菌i经过趋化循环后的适应度值用来表示该细菌i的健康度量。健康度量衡量了其整个寿命中使用了多少营养，以及成功避免有毒物质的能力。按照健康度量升序排列细菌Ohealth（更高的适应度值意味着更低的健康值）。

2）淘汰具有较低健康值的细菌，并保留具有较高健康值的细菌进行分裂，繁殖产生的副本放置在与其父本相同的位置。

步骤7如果k＜Nre，转至步骤3。由于在这种情况下未达到指定的繁殖代数，故启动下一轮趋化循环。

步骤8对于细菌i，以迁徙概率Ped来移动每个细菌，保持群体中细菌数量不变。即：若要淘汰一个细菌，则需将另一个细菌分散到该优化域上的随机位置即可。如果l＜Ned，则转到步骤2；否则，结束算法。

3.4 自适应步长

BFO中，趋化性是一种觅食策略，细菌试图爬到营养浓度高的地方，并避免有害物质。在传统BFO中，趋化循环中的步长是固定不变的，这使其前期寻优速度慢且后期收敛精度低［16］。为此，本文提出了一种自适应步长，即趋化步长随着当前适应度值的改变而变化，使其提供更好的收敛能力。对于第i个细菌，其步长C（i）表达式为

式中：ψ为大于0的常数，ji（θ）为第i个细菌的适应度函数值。如果ji（θ）趋于0，则C（i）→0；如果ji（θ）趋于变大，则C（i）→1。这意味着处于有毒物质附近的细菌具有较高的适应度值。因此，需要赋予其较大的步长来快速迁移到营养浓度较高的地方。

4 仿真及分析

4.1 仿真设置

在Simulink环境里构建电机模型和控制系统仿真，表1为构建的PMSM模型参数。本文中，PI速度控制器的基本设计要求为峰值超调po%＜3%，上升时间tr＜0.02 s，稳定时间ts＜0.8 s，稳态误差ess＜0.2。

表1 PMSM参数设置

对于分数阶PI控制器参数，设置KP的变化范围为0～1，KI的变化范围为0～10，α是变化范围为0～1的分数。

对于BFO和IBFO算法参数，设置为：S＝10、

Nc＝5、Ns＝4、Nre＝2、Ned＝2、Ped＝0.25、ψ＝180、C1＝C2＝2、wφ＝0.7。每种算法进行100次迭代，以获得最优参数组合解。

4.2 速度响应

首先，利用传统梯度下降法、传统BFO算法和提出的IBFO优化算法，根据电机模型对分数阶PI速度控制系统进行参数优化，所获得的最优参数值如表2所示。为了公平比较，速度控制器均采用分数阶PI控制器。

表2 各种优化方法所获得的最优分数阶PI控制器参数

然后，将3种参数优化方法所获得的最优参数配置到分数阶PI速度控制器中。为了验证这些参数的有效性，分别进行电机启动和负载变化仿真，观察控制器的性能。实验中，设置电机启动时的参考速度为1 000 r／min，并在t＝1.5 s时对电机施加1个负载，负载转矩为TL＝10 N·m。3种PI速度控制器的电机转速响应曲线如图6所示。

图6 3种参数优化方法下的PI速度控制器速度响应曲线

分析图5发现：基于传统梯度下降法的分数阶PI控制器的控制性能最差，在电机启动时存在较大的超调量，且稳定到参考速度的时间较长。另外，当电机转矩发生变化时，该方法也不能较好地应对。对于经过传统BFO参数优化后的分数阶PI控制器，其在稳定性和超调量方面要明显优于梯度下降法，但其稳定速度所需的时间依然较长。而通过本文提出的IBFO优化后的分数阶PI控制器，其在启动时获得稳定速度所需的时间最短，且在负载变化时，对速度的影响最小，具有最好的鲁棒性。

为了进一步比较3种方法优化分数阶PI速度控制器的性能，进行3次同样的实验，分别统计速度控制的平均上升时间、峰值超调、稳定时间和稳态误差，结果如表3所示。

通过具体的性能参数可以看出：提出的IBFO优化分数阶PI控制器在各项性能方面都获得了最佳表现，特别是在超调量和稳态误差方面。这是因为，本文在IBFO中的适应度函数中融入了ITAE和超调量因素，并以此来获得最佳的控制器参数。

表3 各种优化方法下的速度控制性能指标

5 结束语

本文提出一种改进型BFO算法用来优化PMSM中分数阶PI速度控制器的3个参数，以此来提高对时变、非线性速度控制系统的控制性能，以及电机负载转矩变化的鲁棒性。将所提方法与梯度下降法、BFO方法进行比较，结果证明了所提方法在上升时间、峰值超调、稳定时间和稳态误差等方面具有较优越的性能，也具有较高的实用价值。

本文中，速度控制器的反馈速度由传统扩展卡尔曼滤波法估计，而反馈速度的准确性直接影响速度控制的性能。为了进一步提高PMSM控制系统的性能，未来将考虑更先进的速度估计方法，以进一步提高速度控制的准确性。