基于PCA和ELM 的表面肌电信号手腕动作识别研究

景甜甜，洪 洁

（1.安徽建筑大学 机械与电气工程学院，合肥 230601；2.安徽江淮汽车集团股份有限公司，合肥 230601）

表面肌电信号（surface electromyogram，sEMG）是肌肉收缩时通过表面电极与相关仪器记录下来的一种能反映人体运动特征的微弱生物电信号［1］。当肢体进行不同的动作时，对应的肌肉收缩也不同，因此，通过对肌肉收缩时产生的表面肌电信号进行处理可以得到不同的肢体动作特征信息，这些特征信息也就成为肢体动作识别的关键。近年来，随着相关技术的发展，表面肌电信号被广泛应用于临床医学、康复医学等领域［2］。

在肌电信号对肢体动作的识别过程中，如何准确地提取肢体动作信息以及选择何种分类器决定着肢体动作识别的准确度。通常，为了获取较高的肢体动作识别率，采集多通道肌电信号并提取相关特征构成高维特征向量。但是这些高维特征向量包含许多无效信息，影响肢体动作识别准确度，且处理复杂。因此，对高维特征向量进行降维，剔除无效信息是一种有效的处理方法。主成分分析（PCA）能在保留有效特征信息的同时对高维数据进行降维，因而在表面肌电信号的处理中被广泛应用［3］。在挖掘出信号的特征信息后，随之就是分类器的选择，它决定着信号识别的准确程度。目前用于肌电信号识别的方法主要有人工神经网络［4］、支持向量机等［5-6］。然而这些方法含有大量的迭代运算，涉及的参数多，往往导致识别精度不高。极限学习机（ELM）作为一种新的算法，具有学习速度快、分类精度高等优点，已经得到广泛运用［7］。

本文基于PCA和ELM算法的优势，将两者结合引入表面肌电信号的手腕动作识别过程中。实验结果表明，该方法能较好地识别内翻、外翻、握拳、展拳等4种手腕动作。

1 PCA原理

PCA降维算法基本思路是：对各维数据进行分析，将数据的主成分（包含信息量大的维度）保留下来，忽略对数据描述不重要的成分，从而实现多维数据的降维处理［8］。其基本原理如下所述。

定义1记x1，x2，…，xm为原始多维变量，y1，y2，…，yn为新多维变量，两者关系如下所示：

在求解式（1）过程中，系数a、i、j的确定原则如下：

1）yi与yj（i≠j；i，j＝1，2，…，m）相互无关；

2）新多维变量数据的方差逐渐减小，s2（y1）＞s2（y2）＞…＞s2（yn）；

从以上的分析可以看出，PCA的实质就是确定原变量xj（j＝1，2，…，m）的主成分yi（i＝1，2，…，n）上的荷载aij（i＝1，2，…，n；j＝1，2，…，m）。

2 ELM 模型

ELM（extreme learningmachine）是一种新型单隐层前馈神经网络算法。相对于传统神经网络，ELM隐含层节点参数可以是随机给定的且不需要调整，学习过程仅需计算输出权重，具有学习效率高和泛化能力强的优点［9］。假设有m个输入变量，n个输出变量，隐含神经元数为a。对于M个训 练 样 本（xi，yi），xi＝［xi1，xi2，…，xim］T，yi＝［yi1，yi2，…，yim］T（i＝1，2，…，M）。

ELM数学模型可表示为

其中：wi＝［wi1，wi2，…，wim］T为输入节点和隐层节点的输入权值；bi为第i层隐层神经元偏差，即阈值；βi＝［yi1，yi2，…，yia］为输出神经元的权值向量；rj＝［rj1，xj2，…，xjn］T为输出阈值。

式中：H为样本隐层输出矩阵，于是转化成求解权值最小二乘解的问题，即

H＋是H的MP广义逆。

3 基于PCA和ELM 的手腕动作sEMG信号识别方法

为了提高手腕动作sEMG的识别准确性，将两者结合起来对采集后sEMG进行降维处理与识别，以获得精度更高、分类效果更佳的分类器。基于PCA和ELM的手腕动作sEMG信号识别流程如图1所示。

图1 手腕动作sEMG信号识别流程

算法实现的过程如下：

1）采集手腕4种动作（内翻、外翻、握拳、展拳）表面肌电信号，每种动作采集M组样本；

2）对采集的肌电信号进行N层小波分解，提取小波系数绝对值最大值作为特征向量，每个信号就有N＋1个特征值，每种手腕动作则有M×（N＋1）阶特征值矩阵；

3）用PCA算法对M×（N＋1）阶特征值矩阵进行降维，设选取的主成分数目为K，此时得到降维后的特征矩阵则为M×k；

4）每种手腕动作选择A个样本作为训练集，剩余的M-A个样本作为测试集，用A个样本对ELM进行训练，建立模型；

5）用训练好的ELM分类器对将M-A个测试样本进行分类测试，输出分类结果。

4 实验与结果分析

实验对象为健康男性志愿受试者。实验选用NIUSB-6211数据采集卡，基于LabVIEW 软件完成手腕4种动作（内翻、外翻、握拳、展拳）两路肌电信号的采集。实验采样频率为1 000 Hz，每个动作采集100组数据，每组2 000个点。采集的一组握拳两路肌电信号如图2所示。

图2 握拳动作两路sEMG信号

用Sym5小波对每组动作的两路肌电信号数据分别做3尺度的分解，分解后提取每级分解的小波系数绝对值最大值：为分解后的子频段，i＝1，2，…，level＋1，此处分解级数level＝3，j为采集通道数，j＝2）构成8维特征矢量：feature＝则每个手腕动作特征矩阵为100×8。

用PCA对上述特征矩阵进行降维处理。为了说明该方法的有效性，分别将原始的8维数据降至二维和3维，降维后的样本分布如图3、4所示。

图3 PCA降维二维分布图

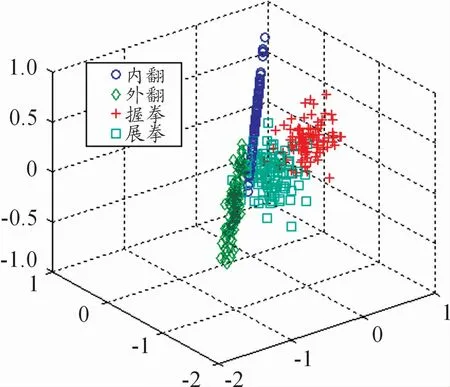
图4 PCA降维三维分布图

从上述图中可以看出，经PCA降维后的手腕4种动作的样本可以被明显地区分开，从而说明了该方法的有效性。下一步将PCA算法与ELM相结合来对手腕4种动作的样本进行分类识别，通过大量实验发现，降至四维时识别效果最好。接下来，随机选择每组手腕动作，选择70组作为训练集，剩下的30组作为测试集。最后，对每个动作设置1个标签，以方便对识别的结果进行观察分析，各动作对应的标签如表1所示。

表1 动作模式识别标签

将降维后的特征数据输入ELM模型中进行测试识别，ELM模型选择Sigmoid函数作为激活函数，隐含层的节点数选择500个。ELM的识别结果如图5所示，为了对比，将原始数据分别降低至二维和三维。用相同的方法输入ELM和支持向量机分类器进行动作识别，识别结果如表2、3所示。

图5 ELM识别结果

表2 ELM分类器识别率 %

表3 SVM分类器识别率 %

由表2及表3可知，运用PCA将手腕动作肌电信号的特征数据降至四维时分类器分类识别率最高；相对于支持向量机，ELM有更好的分类识别率。因此，运用PCA＋ELM组合对手腕动作肌电信号进行分类识别不仅能对不同动作进行准确地识别，还具有着较好的识别率。

5 结束语

基于主成分分析和极限学习机算法在模式识别方面的优势，提出了一种将两者结合起来的方法用于手腕动作sEMG信号识别。首先采集手腕动作肌电信号，提取小波系数绝对值最大值作为原始高维特征向量，然后采用主成分分析对原始高维特征矩阵进行降维处理，最后运用极限学习机对降维后的特征进行分类识别。由实验结果可知，该方法不仅能有效地降低sEMG特征空间维度，还能准确地识别手腕sEMG信号，是一种有效可靠的手腕动作sEMG信号识别方法。