2.3.1 等比数列 教学设计

辽宁省抚顺德才高级中学 韩 娇

一、教学目标

（一）知识与技能

1.通过类比，理解等比数列的概念并学会简单应用.2.通过类比，掌握等比中项的概念并会应用.

3.通过类比，掌握等比数列的通项公式并了解其推导过程.

（二）过程与方法

探索并掌握等比数列的定义，等比中项的概念以及等比数列的通项公式，能在具体的问题情境中，发现数列的等比关系，提高数学建模能力；

（三）情感、态度与价值观

通过对有关实际问题的解决，充分感受数列是反映现实生活的模型，体会数学是来源于现实生活，并应用于现实生活的，数学是丰富多彩的而不是枯燥无味的，提高学习的兴趣激发学生学习的兴趣.

二、教学重点：等比数列的定义和通项公式.

三、教学难点：等比数列的证明

四、教具：多媒体课件、黑板

五、课型：新授课

六、课时：第1课时

七、教材分析

本节课主要的学习内容是等比数列的概念及通项公式，它既是等差数列后的又一个特殊数列，是研究数列的重要载体，与实际生活有密切的联系，如银行贷款，细胞分裂需要用等比数列知识来解决，在研究过程中体会了由一般到特殊的数学思想，函数思想，方程思想，在高考中占有重要的地位。

八、学情分析

对于等比数列的定义学生相对易理解，但对于从实际问题中抽出来等比数列的模型会存在一定困难，以及一些计算的化简的能力要求较高，对于等比数列的证明理解上会有一定困难。

九、教学过程

（一）问题导学

知识点一 等比数列的概念

(5min)教师提问：观察下列4个数列，归纳它们的共同特点？

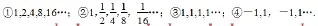
学生回答：从第2项起，每项与它的前一项的比是同一个常数.

知识梳理：等比数列的概念和特点.

(1)文字定义：一般地，如果一个数列从第____项起，每一项与它的____一项的____都等于____常数，那么这个数列叫做等比数列，这个常数叫做等比数列的____，通常用字母q(q≠0)表示.

(3)等比数列各项均_____为0.

知识点二 等比中项的概念

(5min)教师提问：在2,8之间插入一个数，使之成等比数列.这样的实数有几个？

教师提问：是任意的两个数都等比中项吗？

学生回答：同号的两个数才有等比中项

知识梳理：等差中项与等比中项的异同，对比如下表：

?

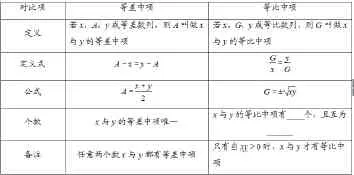
知识点三 等比数列的通项公式

(5min)教师提问：等差数列通项公式是如何推导的？你能类比推导首项为a1，公比为q的等比数列的通项公式吗？

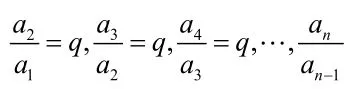
将上面n－1个等式的左、右两边分别相乘，

当n＝1时，上面的等式也成立.

∴an＝a1qn－1(n∈N＋).

知识梳理：等比数列{an}首项为a1，公比为q，则an＝a1qn－1.

（二）例题讲解（略）

（三）当堂训练（略）

（四）总结

1.等比数列的判断或证明

(2)利用等比中项：an+1=anan+2(n∈N＋).

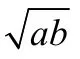
3.等比数列的通项公式an＝a1qn－1共涉及a1，q，n，an四个量，已知其中三个量可求得第四个量.此部分教师总结

十、教学反思

本节课的重要思想采用类比的思想，在教师的引导下，以学生为主体完成整个课堂教学，学生的引导比较到位，重点突出，实现了预期目标，但基础较好的学生反映课堂题较简单，练习题层次上没有太多差异，不能满足各个层次的需求，因此以后教学应该在习题上下功夫。