融入H指数的局部拓展类重叠社区发现算法
朱征宇,袁 闯
1(重庆大学 计算机学院,重庆 400044)2(软件理论与技术重庆市重点实验室,重庆 400044)
1 引 言
随着信息技术的发展,网络在现实世界无处不在.在2002年Girvan和Newman等指出在网络中广泛存在着社区结构[1],网络由若干个群或者团组成,每个群团内部之间联系紧密,而不同群团之间联系相对比较稀疏.社区发现可以帮助我们了解网络的结构、相互之间的作用和分析网络的特征,因此网络社区发现正在越来越受人关注,有了越来越多的应用.
目前已经存在了很多经典的社区发现算法,主要分为非重叠社区划分和重叠社区划分.非重叠社区发现方法和重叠社区划分算法发现的区别主要在于社区中的节点是否可以属于多个社区.在实际网络中,社区之间不是孤立的,是相互重叠和互相交叉的,一个节点不仅仅属于一个社区,是可以属于多个社区的,如一个人可以有多个兴趣小组、科研工作者的研究领域会有交叉、在社交网络中,一个用户会有多个朋友圈等,因此重叠社区发现的研究更有现实的意义.
随着近些年重叠社区发现的研究得到越来越多的关注,已经在该方向取得了很多研究成果.Palla等[2]人2005年提出了基于派系过滤算法CPM,通过团过滤算法来识别网络中的社区结构,将社区看作一些互相连通的子图构成的集合,基于clique扩展的算法有[3,4];stave等[5]在通过对LPA(label propagation algorithm)扩展,提出了多标签传播的算法COPRA[6],初始给每一个节点分一个标签,根据邻居节点的标签更新标签,最后标签相同的划分为同一个社区,CRD-LPA[7]和LRDC[8]通过节点重要性在标签传播阶段选择标签,提高了算法的稳定性.Lancichinetti 等[9]在2009提出了基于了局部优化和扩展的算法LFM,开始随机选取网络中的初始节点作为种子,通过局部适应度函数进行社区扩张,直到适应度函数为负时停止,各个社区扩展独立进行,各个局部社区综合起来形成网络整体的重叠社区,代表算法有DEMON[10],LOC[11].虽然社区划分算法已经取得了一定的研究,但是随着信息的发展,网络的结构也越来越复杂,如何准确快速的发现网络中的重叠社区,仍然是一个具有挑战性的课题.
在2016年,LYU等[12]研究发现H指数不仅能很好的衡量网络节点重要性,且通过仿真实验发现,指数在许多情况下可以更好的量化节点的影响.LFM等局部拓展算法为随机选种,造成算法的不稳定性,文献[13,14]通过节点重要性的强弱来判断其邻接节点是否加入自己的社区,仅仅考虑了邻接节点重要性对节点的影响,而没有考虑节点加入新社区后节点的重要性变化.本文的主要思想是先通过H指数和局部影响力计算节点的重要性,之后按节点重要性进行排序,选择更重要的节点作为初始种子节点,使算法具有稳定性并提高了效率;之后通过考虑邻接节点的重要性和自身在新社区中的重要性作为节点的适应度,将其利用在社区拓展上,社区拓展时计算节点的适应度,大于阈值的加入社区,使划分更加合理和高效.
本文的创新点有两点:
1)提出了一种新的节点重要性计算方法.
2)提出了一种新的适应度计算方法,不仅考虑了节点周围点的重要性,也考虑了节点自身加入社区后的重要性.
2 基本概念和算法
2.1 基本概念
定义1.(节点的度)通常,社会网络可以由G=(V,E)的形式表示,其中V={v1,v2,…,vn}表示节点的集合,E={e1,e2,…,en}表示边的集合,节点的度表示为
(1)
如果节点i和节点j有边相连则δij为1,否则为0.
定义2.(节点的局部重要性)我们先求出每个节点邻接节点度的和,然后得到其中的最大值,最后用最大值归一化节点邻接节点度的和,节点局部重要性具体公式为;
(2)
其中i表示求节点重要性的节点,j表示节点i的邻接点,N(i)为节点i的邻接节点集.
定义3.(节点在社区中的局部重要性)根据定义2,局部重要性与邻接节点有关,节点在加入社区后,节点在社区中的邻接点数量比没加入之前要少,我们定义在社区中的局部重要性为
(3)
Nc(i)
表示节点i在社区c中的邻接节点集,对公式2变化为,把j的范围j∈N(i) 变为j∈Nc(i).
定义4.(节点的重要性)根据公式2,再引入H指数[10]提出了节点重要性IM(i)
IM(i)=H(kj1,kj2…kjki)+lo(i)
(4)
Ki为节点i 的度.j1,j2…为节点i的邻接节点,Kj1,Kj2… 为节点j1,j2的度,即H指数这里主要作用在节点的邻接节点的度上.H指数为节点的邻接节点度中有h个节点的度大于h,其他节点的度小于或等于h.
定义5.(节点在社区中的影响力)我们定义在社区c中节点i的影响力为IMc(i)
(5)
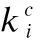
定义6.(节点的适应度)我们定义节点i对社区c的适应度fn(i,c)为
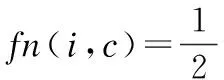
(6)
其中N(i)为节点i在图中的邻接点集合,Nc(i)为节点i在社区c中的邻接节点集,适应度fn(i,c)反应了节点i和社区c的紧密程度,fn(i,c)越大则联系越紧密,反之越松散.
2.2 算法描述
输入:G=(V,E)
输出:社区集合C={C1,C2…Cq}
Step1.初始化节点
在初始化阶段把所有节点标记置为F,表示未被访问,然后先使用公式(1)计算所有节点的度,再用公式(3)计算所有节点的重要性IM(i),并将其按照从大到小排列.
Step2.挖掘种子社区
1)IM(i)大的节点更重要,可以作为中心节点进行社区扩展,因为IM(i)已经从大到小排好序,所以按顺序选择标记为F的节点作为种子节点和种子社区ci,并将其标记为T,表示已被访问.
2)把种子节点邻接的所有节点,不管是否被访问,都添加到社区ci,并将这些节点标记为T.
3)使用公式(6)计算社区ci所有节点的在社区ci中的适应度fn(i,c),如果适应度小于阈值α,则将其剔除种子社区ci,查看此节点是否还属于别的社区,若没有则设置其为F.
4)回到3)重新计算种子社区所有点的适应度,直到社区ci中的所有节点适应度都大于阈值α.
Step3.种子社区扩展阶段
1)将种子社区ci的所有邻接节点,不管是否被访问,每次添加一个节点到种子社区ci中,记这个节点为j.
2)在添加之后,使用公式(6)计算节点j在社区ci中的适应度fn(j,c),如果其适应度大于阈值α,则将其添加到社区ci中,并且若是节点的标记为F,则置为T,将种子社区ci的邻接节点都计算一遍.
3)若添加到社区ci的节点数大于1,表示有节点加入到社区,社区有新的邻接集合,重新得到社区的邻接集合,再回到(1)开始计算,直到没有节点添加到社区ci中.
Step4.迭代
重复Step 2,Step 3,直到没有节点的标记为F,则停止.
Step5.合并社区
有的节点可能周围有多个社区,每个社区对其的适应度都小于阈值α,所以会出现一个社区只有一个节点的情况,即孤立节点,我们对孤立节点的处理是重新计算孤立节点周围社区的适应度,将其加入适应度值最大的社区.
2.3 算法分析
2.3.1 重叠节点分析
由于在挖掘种子社区和种子社区拓展时,添加节点时并不考虑此节点是否已经加入其它社区,只要满足大于适应度阈值即可,可以使一个节点加入多个社区,所以是可以产生重叠节点的.
2.3.2 稳定性分析
对比LFM算法我们可以发现,由于LFM算法随机选取节点作为种子节点,所以造成算法具有不稳定性,我们的算法每次选取影响力最大的点作为种子节点,提高了算法的稳定性.
2.3.3 时间复杂度分析
1)计算节点的重要性包括计算H指数和局部影响力,用时为O(n*k*lgk),其中n为节点数量,k为节点的度.对节点按照重要性排序,使用快速排序时间复杂度为O(n*lgn).
2)挖掘种子社区,需要计算社区内所有节点的适应度函数,用时为O(k2*lgk),设社区个数为nc,所以最后用O(nc*k2*lgk).
3)种子社区扩展,由内向外每次拓展一个节点,每次添加节点要计算节点的适应度,设每个社区大小为m,则用时O(nc*m*k*lgk).
4)后处理计算孤立节点属于邻接社区的适应度,主要与孤立节点的个数有关,所以总用时为O(p*k*lgk),其中p为孤立节点个数.合并相似性时间复杂度主要与社区数量有关,时间复杂度为O(nc*nc).
综上所述,由于p要小于社区个数nc,所以算法时间复杂度为
max(O(n*k*lgk),O(n*lgn),O(nc*k2*lgk),
O(nc*m*k*lgk),O(nc*nc))
3 实验分析
本节将验证HDOC算法的性能.我们将HDOC算法分别与其他几种具有代表性的重叠社区发现算法进行比较,对于COPRA[6],LFM[9],QLFM[15]算法我们采用原作者提供的实现源码;LPPB[16]和OMKLP[17]我们采用原作者论文中的数据;对于COPRA算法我们选取v=2;QLFM算法中使用的系数,我们取原作者在论文中的数据0.9;对于本算法的阈值以下实验我们都设置为α=0.5,在3.3节我们将证明选择此值的原因.由于COPRA、LFM和QLFM都具有不稳定性,所有我们对这三种算法运行10次取最好结果,本算法为稳定算法,所以只需要运行一次.我们首先比较了采用不同的α取值对HDOC算法结果的影响;然后在真实网络中,对上述几种算法的社区发现质量和时间效率进行了对比,在社区发现质量方面,我们采用了两种模块度算法来评价;最后我们在人工网络中比较了上述几种算法的社区发现质量.
3.1 实验环境
笔记本,处理器Inter(R)Core(TM)i5 2.50GHz,内存2G,350G硬盘,操作系统为32-bit win10,编程语言为java,开发环境为Intellij IDEA2016.
3.2 评估方法
在社区发现的研究中,有两种方式对算法进行评估.
一种是使用现实网络中的数据集对算法进行测试,由于真实网络结构的真值是未知的,一般使用模块度函数作为评价标准,在这里我们为了更好的评估算法的性能,选择了两种模块度评价标准:分别是Shen等[18]在2009年提出的扩展模块度函数EQ和Nicosia等[19]在2009年提出的重叠模块度指标Qov.
另一种方式是使用LFR基准网络进行测试,由于基准网络社区网络结构的真值是已知的,所以采用社区识别精度的评价指标为标准互信息量(NMI,normalized mutual information)[9]作为评价指标,其中NMI值越大,说明算法识别社区结构的准确率越高,反之越低.
3.3 参数的选取
为了探究阈值α对模块度的影响,我们选择在四种不同规模的真实网络中设置不同的α观察模块度的变化情况,这里的模块度使用Qov,由于HDOC为稳定算法,所以在每个网络中只做一次实验.α取值为从0.3开始到0.7,每次增长0.05,实验结果如图1,在α取0.5时,Qov值最大,在四种网络中获得的重叠社区结构最佳,因此我们取α为0.5.以下在真实网络和LFR基准网络中的实验α都取0.5.
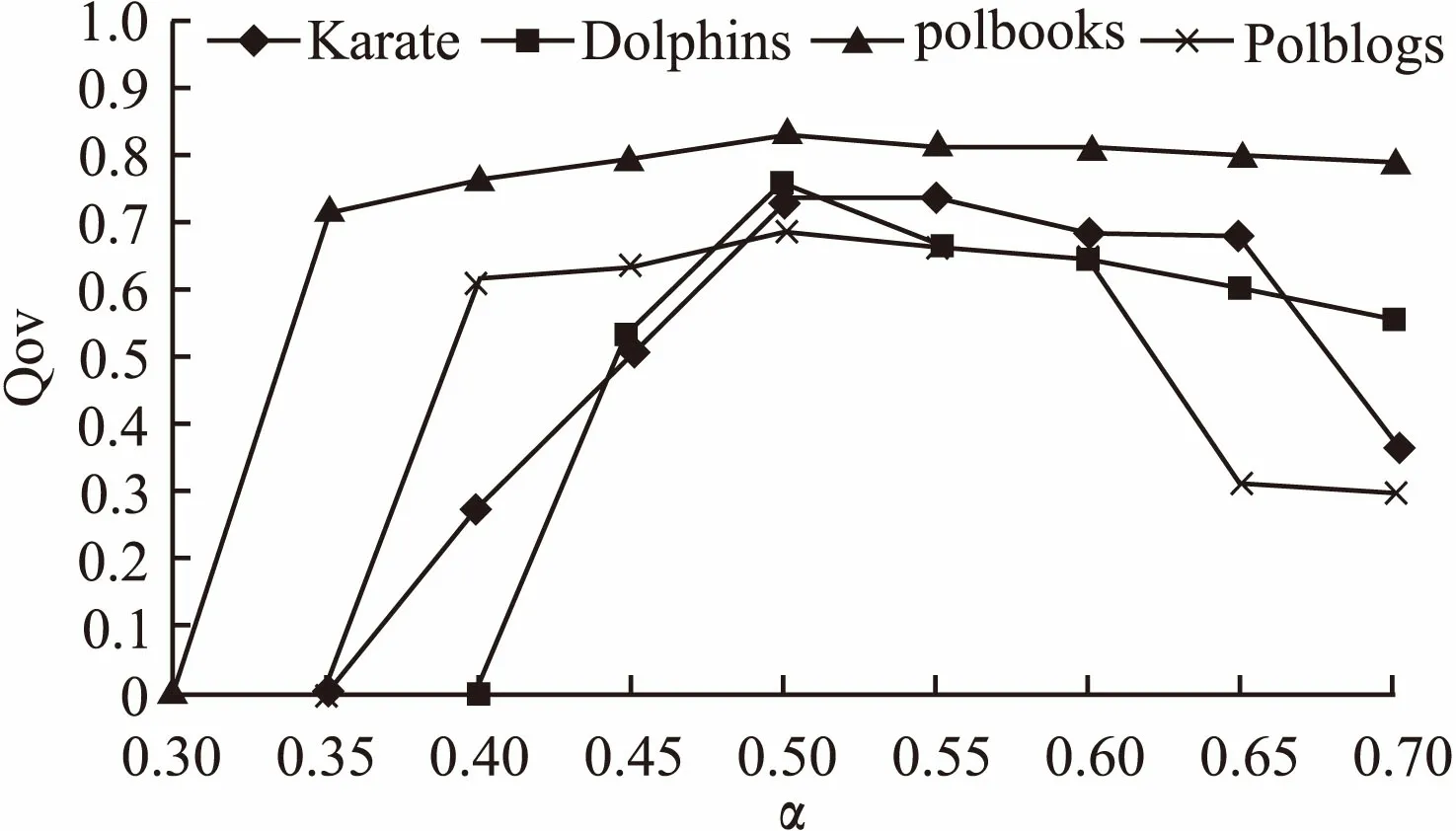
图1 不同阈值下的Qov值Fig.1 Qov values under different thresholds
为了验证在真实网络中阈值α的普适性,我们又在四种不同的LFR基准网络中进行了验证,我们选择了由不同的社区大小、混合比例数、每个重叠节点属于社区的个数形成的四种类型网络,其中四种类型的网络规模相同,最后的划分结果使用标准信息量NMI评价,由于LFR基准网络是随机生成的,所以我们对于每种网络随机生成了10次,然后取10次实验NMI评价的平均值.表1是四种类型网络的具体参数.
表1 四种不同的LFR基准网络
Table 1 Four different kinds of LFR networks

IdNkmarkmincmaxconommuS110001050105010020.1S2500010502010010020.1S310001050105010020.3S450001050105010080.1
通过图2看出,通过LFR基准网络随机形成4种不同类型的网络,在α取0.5时网络划分结果的NMI值最大,即算法划分的结果与真实的社区更为接近,说明算法的阈值α取0.5社区划分的效果最好.通过真实网络和随机生成的LFR基准网络的实验,α都为取0.5划分结果最优,所以α取0.5时算法划分社区的效果最好,且取值具有一定的普适性.
3.4 真实网络数据集
表2列出了实验用到的10种真实网络数据集,表3和表4分别表示各算法用Qov和EQ的评估结果,表5表示各算法在几种真实网络数据集中的运行时间.由于没有LPPB和OMKLP算法的源码,我们使用了原作者在论文的实验数据,
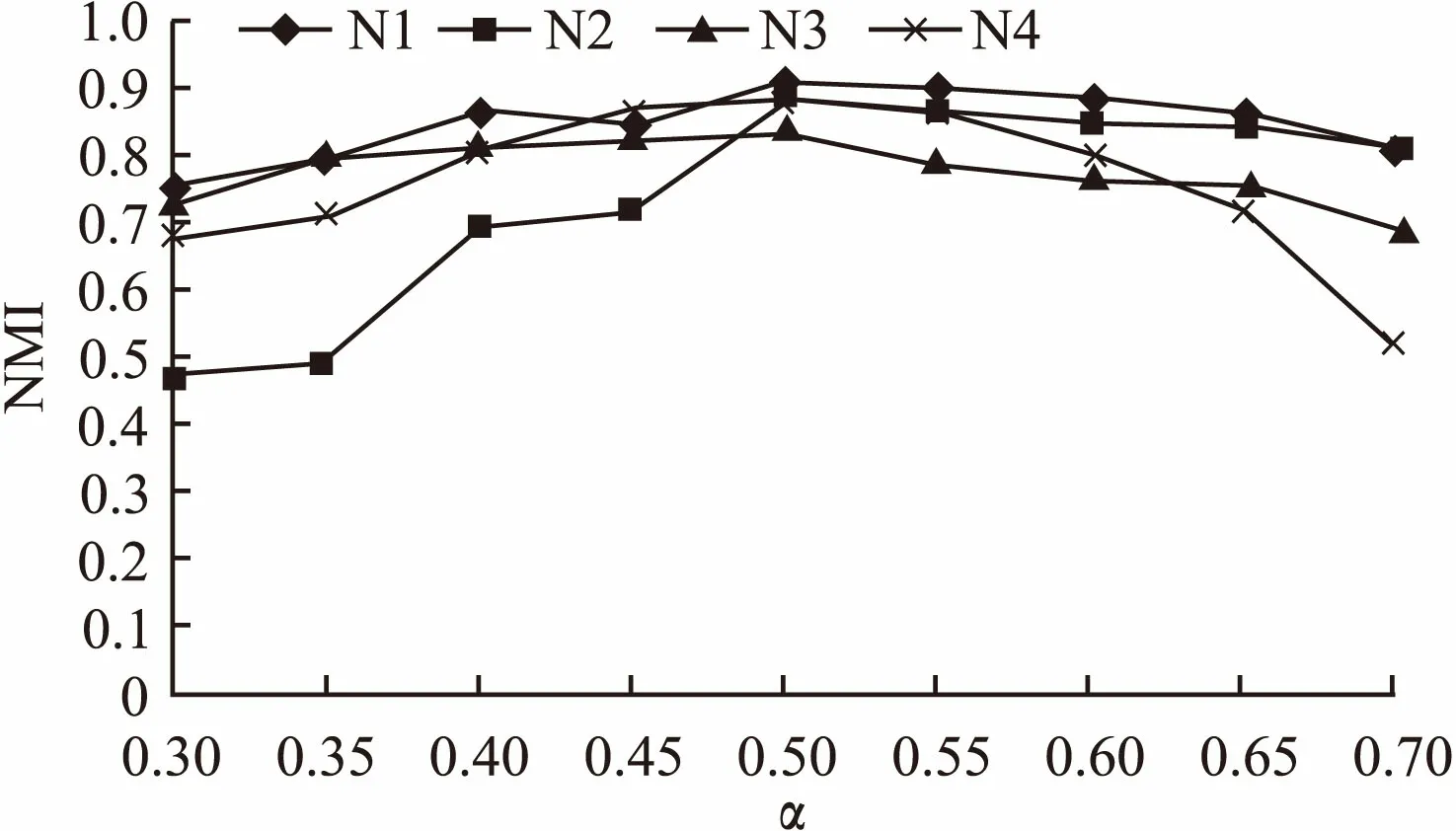
图2 阈值对四种LFR网络的影响Fig.2 Effect of threshold on four kinds of LFR benchmark networks
在算法时间对比时,考虑电脑性能不同,没有使用这两种算法的时间数据.LPPB算法的原作者在论文中只列出了4种网络中Qov评估的实验结果,OMKLP算法的原作者在论文中列出了9种网络中EQ评估的实验结果,所以在用Qov评估时,HDOC、LFM、COPRA、QLFM只在4种网络中实验.用EQ评估时,只在9种网络中实验.对于LFM、COPRA、QLFM算法,均取原作者的源码进行实验,由于这几种算法都是不稳定算法,所以取10次中最好结果.
表2 真实网络数据
Table 2 Real network data
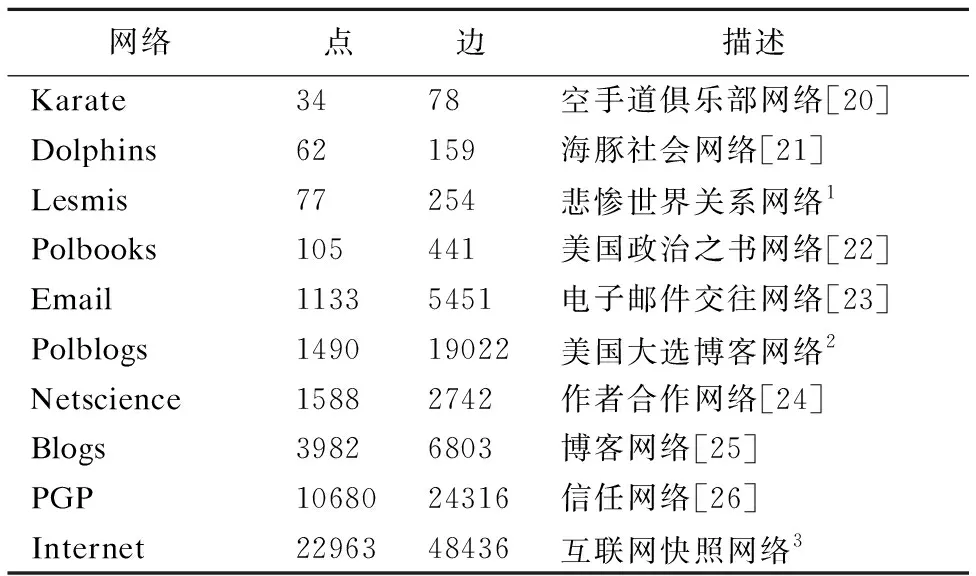
网络点边描述Karate3478空手道俱乐部网络[20]Dolphins62159海豚社会网络[21]Lesmis77254悲惨世界关系网络1Polbooks105441美国政治之书网络[22]Email11335451电子邮件交往网络[23]Polblogs149019022美国大选博客网络2Netscience15882742作者合作网络[24]Blogs39826803博客网络[25]PGP1068024316信任网络[26]Internet2296348436互联网快照网络3
通过表3可以看出,在Karate、Dolphins、Blogs、PGP四种网络上用Qov对比时,我们的算法在四种网络上比QLFM、LFM、COPRA算法的最好值要好,比LPPB算法的模块度平均值要好.通过表4可以看出,HDOC在Karate、Dolphins、Polbooks、Eamil、Netscience、PGP、internet这7种网络EQ值为第一;Polblogs网络中EQ值第二,仅略低于COPRA,取得次优值;Lesmis网络中,划分效果较差.综上可知,分别用两种模块度函数比较,HDOC效果较好,在真实网络中具有较强的社区识别能力,并且适用的网络较为广泛.
表5中LFM、COPRA、QLFM算法由于是不稳定算法,需要运行10次取最好结果,所以表中数据为运行10次所用时间,HDOC稳定性较高,数据为算法一次运行时间.通过表中数据我们可以看出在10种网络上,本算法与其他三种算法对比,速度明显较快,时间效率较高.
表3 Qov实验结果
Table 3 Results of the Qov test
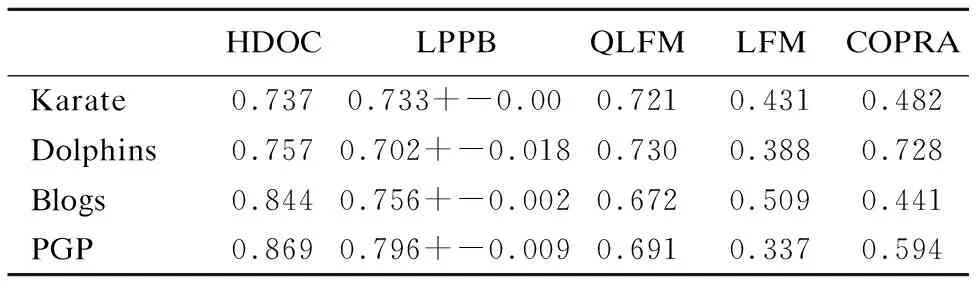
HDOCLPPBQLFMLFMCOPRAKarate0.7370.733+-0.000.7210.4310.482Dolphins0.7570.702+-0.0180.7300.3880.728Blogs0.8440.756+-0.0020.6720.5090.441PGP0.8690.796+-0.0090.6910.3370.594
3.5 LFR基准网络数据集
LFR基准网络的包括以下参数:N表示节点个数;k表示网络中节点的平均度;mark表示节点的最大度;minc表示最小社区包含的节点的个数;maxc表示最大社区包含的节点的个数;on表示重叠节点的个数;om表示每个重叠节点所属的社区的个数;mu为混杂系数,mu越小说明社区越清晰,否则社区结构越模糊.
表4 EQ实验结果
Table 4 Results of the EQ test
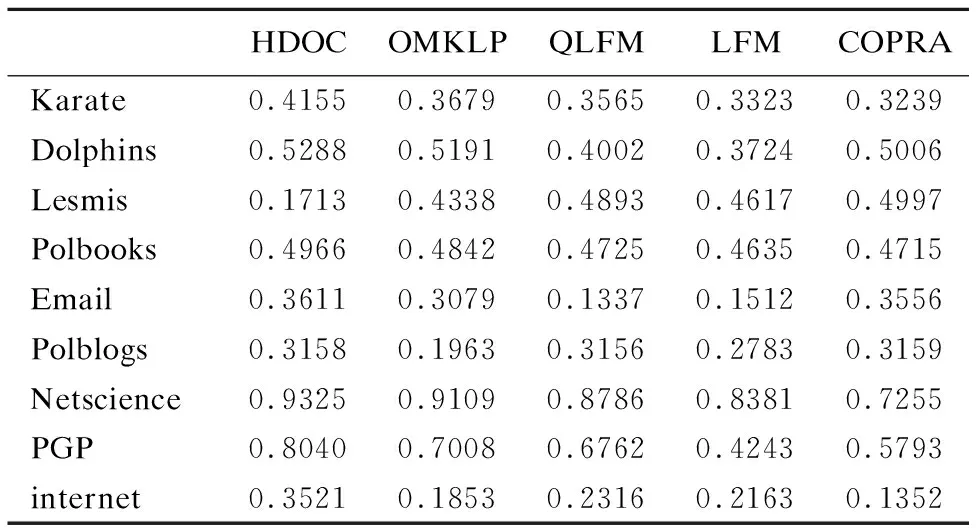
HDOCOMKLPQLFMLFMCOPRAKarate0.41550.36790.35650.33230.3239Dolphins0.52880.51910.40020.37240.5006Lesmis0.17130.43380.48930.46170.4997Polbooks0.49660.48420.47250.46350.4715Email0.36110.30790.13370.15120.3556Polblogs0.31580.19630.31560.27830.3159Netscience0.93250.91090.87860.83810.7255PGP0.80400.70080.67620.42430.5793internet0.35210.18530.23160.21630.1352
表5 各算法运行时间(ms)
Table 5 Runtime of each algorithm
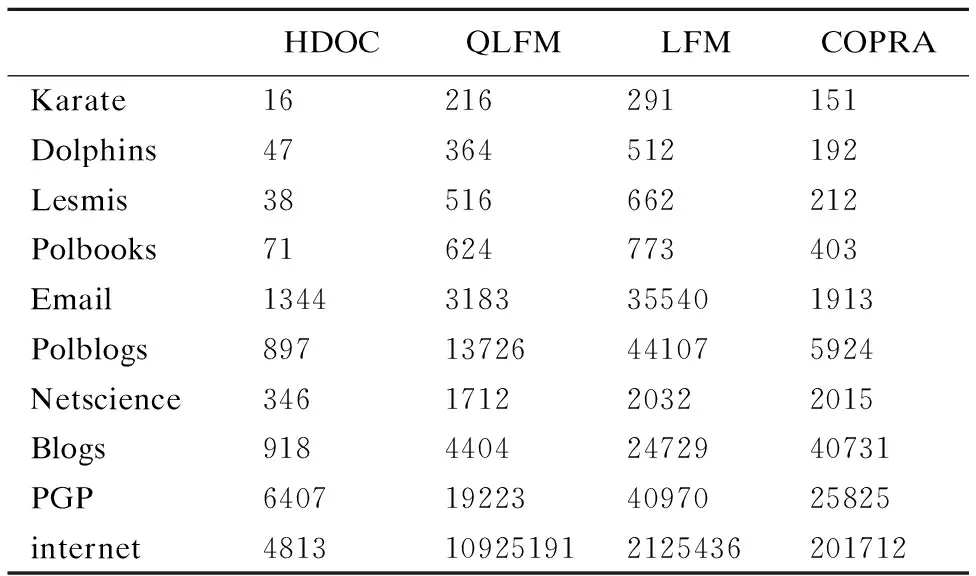
HDOCQLFMLFMCOPRAKarate16216291151Dolphins47364512192Lesmis38516662212Polbooks71624773403Email13443183355401913Polblogs89713726441075924Netscience346171220322015Blogs91844042472940731PGP6407192234097025825internet4813109251912125436201712
为了比较各种算法在不同类型网络下的社区发现质量,我们根据网络的规模、混杂系数mu及每个重叠节点所属的社区的个数om这三个维度来生成不同类型的网络,各网络的具体参数见表6.
LFM、QLFM、COPRA算法及我们的HDOC算法在4组LFR网络中的实验结果见下图,横坐标为混杂系数mu,纵坐标为社区发现质量NMI.通过图3、图4可以看出随着混杂系数的增大,HDOC和其他算法一样NMI越来越小,说明社区发现的质量越来越差,在mu大于0.4之后表现尤为明显,已经不能发现有意义的社区.和其他算法对比,在不同规模的网络中,HDOC在mu小于0.4时,NMI明显大于其他算法,在mu大于0.4后,在大型网络中HDOC算法较COPRA效果要差,比LFM和QLFM算法要好.
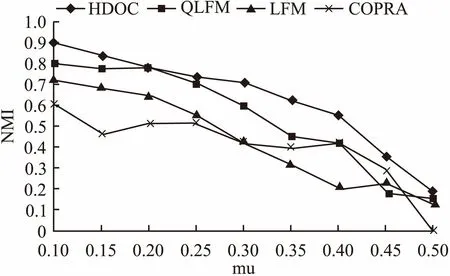
图3 针对S1网络识别结果Fig.3 S1 network recognition results
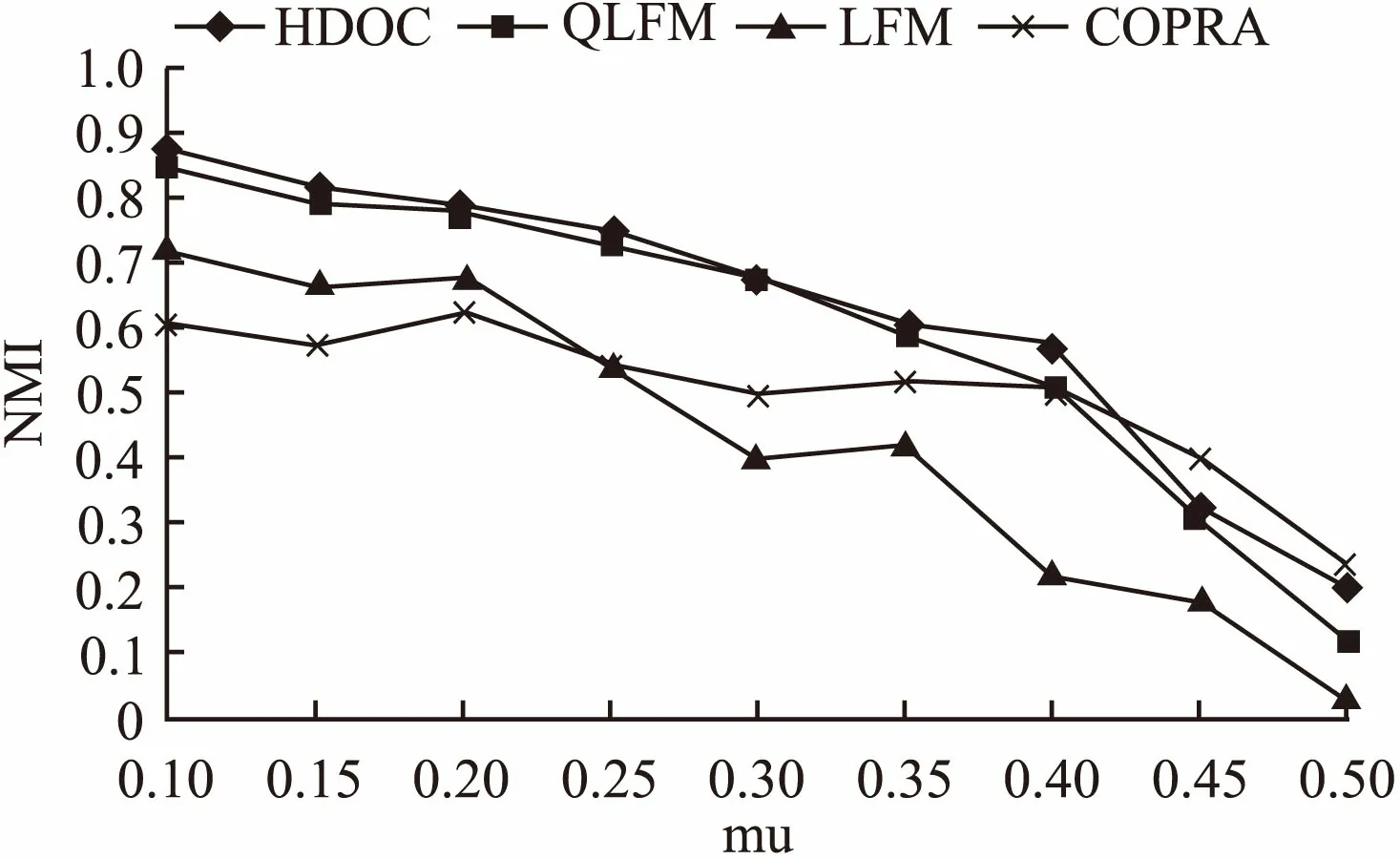
图4 针对S2网络识别结果Fig.4 S2 network recognition results
对于不同重叠度的网络,我们可以从图5、图6看出HDOC随着om的增大,NMI会随之减小,但是HDOC算法的NMI值一直大于其他算法三种算法的NMI值,划分效果较好好.和其他三种算法对比,随着om的增加,HDOC对于社区识别精度的影响不大,表现明显比其他算法要好.
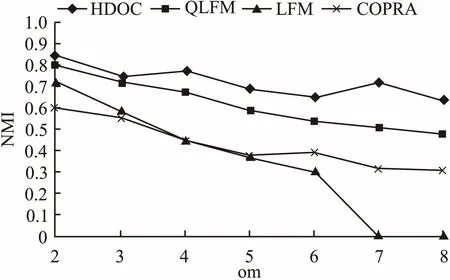
图5 针对S3网络识别结果Fig.5 S3 network recognition results
综上,除了在大型网络、社区清晰度较低时,HDOC表现比COPRA较差,在不同重叠度、不同大小、不同社区清晰度的网络中,HDOC表现比其他三种算法要好,所以从整体来说,HDOC可以在人工合成网络发现高质量的社区.
表6 LFR基准网络信息
Table 6 Information of LFR benchmarks
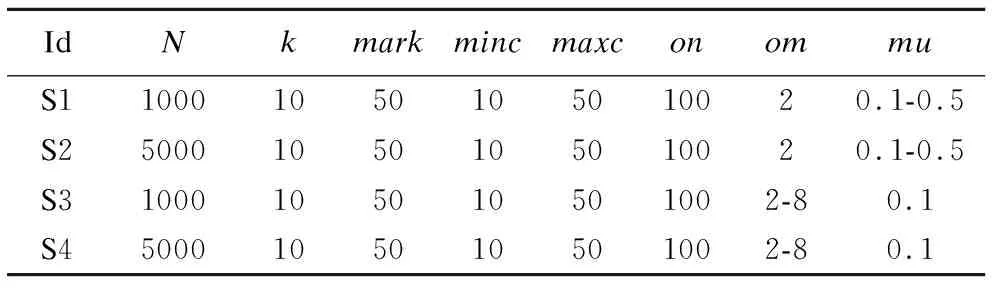
IdNkmarkmincmaxconommuS110001050105010020.1-0.5S250001050105010020.1-0.5S31000105010501002-80.1S45000105010501002-80.1
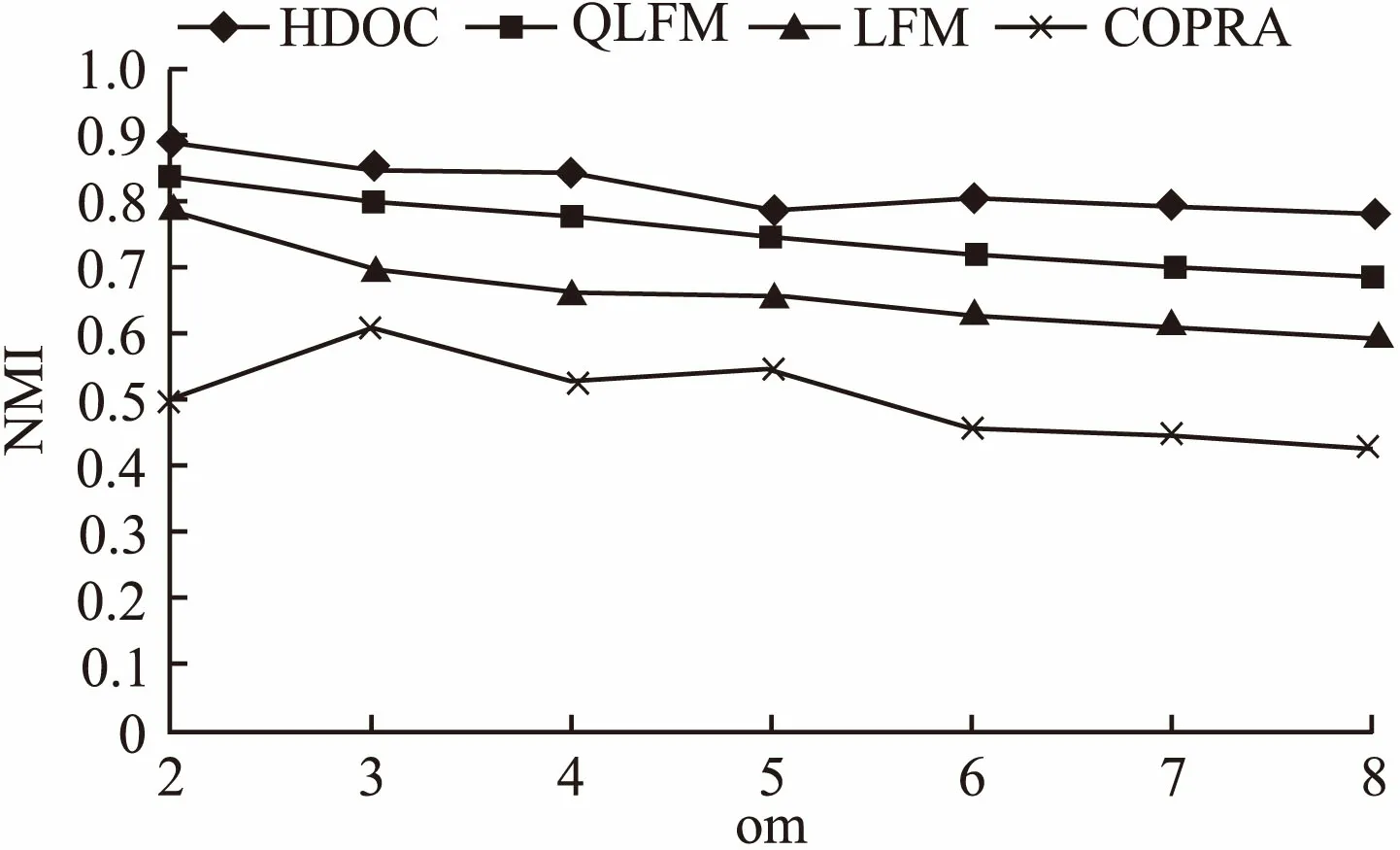
图6 针对S4网络识别结果Fig.6 S4 network recognition results
4 结 论
本文将通过H指数和局部影响力计算出的节点的重要性融合到种子扩展的思想中去,并在拓展时提出了一种新的适应度函数,不仅考虑周围节点的影响力,也考虑节点在社区中的影响力.对比传统的种子拓展类算法,通过节点重要性选种,提高了算法效率,并解决了随机性.一般利用节点影响力的算法都是考虑邻接节点的重要性,本算法也考虑了自身在社区中的重要性,使划分更加合理.通过在真实网络和人工网络与其他算法的对比,本算法的Qov和EQ都比较理想,时间效率对比传统算法也有明显提升.
未来的研究工作集中在:
1)种子社区内部的点联系应该更加紧密,所以可以分别调整挖掘种子社区和种子社区拓展的适应度阈值进行实验,选择适合的阈值.
2)对于适应度阈值的设置通过实验得出,可能不是最优解,而通过网络的结构计算出来,这样阈值的设置可能会更加精确一点,使划分的效果会更好.

