信息物理融合系统建模的区间GMDH算法
任胜兵,黄 飞,刘 媛
(中南大学 软件学院,长沙 410075)
1 引 言
信息物理融合系统[1](Cyber-Physical System,CPS)是集计算系统与物理系统于一体的下一代智能系统,通过嵌入式系统与网络实现了两者之间的实现深度融合与实时交互[2].未来CPS将广泛应用于重要基础设施的监测与控制、智能交通系统、智能高速公路、智能电网和智慧医疗等诸多领域.CPS自被美国国家委员会提出以来,受到了各国政府的广泛关注,美国总统科学技术顾问委员会(NSF)把CPS列为关键的研究领域之一,并举办了一系列关于CPS的研讨会.自2006年提出至今,CPS的发展得到了许多国家政府的大力支持和资助,成为学术界、科技界研究的重要方向.
由于离散的计算过程与连续的物理过程并存于CPS之中,两者之间的融合特征很难能够用单一的模型进行刻画.且CPS具有的时空特性和动态非确定性,现有的建模语言也难以适应.因此,如何建立可靠的CPS模型成为研究和应用CPS的瓶颈.
本文在数据驱动建模方法的基础上,将模型的参数估计问题看成是一个集合反演问题,结合区间分析思想,提出了区间GMDH(interval Group Method of Data Handling,iGMDH)算法.由于集合反演求解的SIVIA(Set Inverter via Interval Analysis,SIVIA)算法采用二分法对估计参数的先验搜索域进行搜索,使得搜索的空间过大,算法的计算量成指数级增加,需要大量的时间和内存,甚至会使二分陷入死锁.为此,本文提出的算法首先对SIVIA算法进行改进,通过引入收缩算子[3]使算法能够在解集保持不变的情况下,对估计参数的区间进行压缩,从而减少计算的时间复杂度和空间复杂度.其次,将GMDH算法的输入及模型计算转变成区间数和区间运算,以区间的形式实现数据的存储和运算,并应用改进后的cSIVIA算法对模型参数进行估计,进一步计算求得区间估计的点估计,并依据外准则对产生的中间模型进行筛选,从而建立最终的系统模型.
2 相关工作
CPS建模是CPS系统研究的热点.伯克利大学的Lee,Edward A通过总结现有的仿真控制建模方法提出了“信息系统物理化和物理系统信息化”的概念[4],来解决物理实体和信息实体的建模以及二者的交互问题.文献[5]将CPS系统精化为计算实体和物理实体,并通过分析UML语言及simulink/RTW建模工具构建计算实体模型和物理实体模型的可行性提出了基于UML框架的两种异质模型融合方法.文献[6]利用AADL对CPS建模进行扩展,给出了一种新的建模语言CPSADL的编译方法.并以月球车辆自主行走系统为例,说明了CPSADL的应用.文献[7]通过深入分析诸如异构、分布式车载CPS软件的特点,提出了一种车载CPS软件的建模方法,以扩展混合自动机为形式化的建模工具,从服务提供的角度出发,分别将监控设备实体置主体作为设备服务.最后,以车辆速度控制系统为例说明了建模方法的有效性.文献[8]通过对现有软件体系结构进行扩展,提出了一种新的CPS体系结构模式,满足了信息物理系统的建模需求,增加了对CPS的物理系统和信息系统之间交互的建模支持.并以锅炉温度控制系统为例,论证了CPS体系结构模式的应用.以上提出的CPS建模方法,在建立模型之前,建模者都需掌握其运行环境及所经状态,以及每个状态转换所需的事件.而随着CPS复杂度的增加,面临环境的日益复杂,在构建系统框架或分析系统时这些方法都变得难以适应.
基于数据驱动的CPS建模是复杂CPS建模的另一类重要方法.通过使用经验数据来对CPS运行过程中的主要属性(自相似、非平稳性)进行描述,根据系统特征从数据中找出普遍规律并建立模型.文献[9]提出了一种从数据出发建立CPS系统模型的方法,从获取的离散数据中提取能够反映系统属性的特征值,运用GMDH算法[10,11]建立系统模型,实现了连续物理事件与离散计算系统的深度融合.GMDH算法是一种启发式自组织的建模方法,它能够根据输入、输出变量原始的信息构造出模型,并利用外准则选取最优模型,实现对研究系统内部结构的模拟.其在结构上具有的自组织、全局选优的特性,使其能够有效地对复杂多变量系统进行辨识[12,13].然而,由于计算机字长有限导致的数据不精确性以及随机噪声引起的数据不确定性,使得计算机在处理程序时得到的浮点计算结果与理论计算之间存在着误差,GMDH算法在进行模型参数估计的过程中,其计算产生的误差,再次参与运算时将在原有的基础上进一步产生误差.尤其是在建立分层模型的过程中不断扩大进而产生误差累积的作用,最终可能得到无效结果.
区间分析[14]是R.E.Moore等人为了研究计算机浮点数运算所产生的误差问题,于上世纪60年代初提出的.区间分析能够以区间的形式实现数据的存储与运算,从而避免浮点运算所产生的误差,保证了计算结果的可靠性.另外,还可以把某些不确定性表述为区间,并直接包含在区间算法之中,可以很好地表示其可行集.因此,区间分析被认为是系统参数估计的一个有力工具.
SIVIA算法作为区间分析在非线性系统参数估计中的经典算法,能够在给定精度内求出参数值的全部全局最优解,并能给出包含最优解且满足要求的任意小区间.文献[15]根据先验知识,实验数据和模型的附属要求将数据与相应模型输出之间的误差包含在已知的可行域中,并描述出了贝叶斯最优置信域.文献[16]提出了一种基于区间分析的有界误差估计方法来识别定向井有杆抽油系统的粘滞阻尼系数和库仑摩擦系数,与传统的估计方法相比,该方法不仅具有全局性且不需要初始化,还能够避免由于测量输出数据的转换而产生的数量误差.文献[17]通过将非线性边界误差估计问题看做一种反演集合,提出了一种根据机器人车载传感器、环境传感器以及其他机器人的实时数据估计移动机器人位置的方法,解决了大型协作环境中移动机器人的定位问题.然而,SIVIA算法在采用二分法对先验搜索域进行搜索时,使得算法需要大量的时间和内存,甚至会使二分陷入死锁.因此,本文提出的算法首先对其进行了改进.
3 基于区间分析的iGMDH算法
GMDH算法通常采用最小二乘估计对建立的模型进行参数估计.但由于观测误差、模型的结构误差以及随机噪声等不确定因素的存在,容易造成输入数据不精确、难以确定的问题.为了解决这个问题,本文通过引入区间分析的算法,将GMDH算法的输入转变成区间数,基于区间进行运算,建立了具有区间参数的CPS系统模型,其具体的建模流程如图1所示.

图1 区间GMDH算法的建模流程Fig.1 Modeling process of interval GMDH algorithm
其中x1,x2,…,x5为系统5个可能的输入变量,对输入变量两两组合之后,运用SIVIA算法进行区间估计得到待估参数的估计集,生成第一层的中间模型u1,u2,…,u10.计算出所得估计集的中心,作为参数估计的点估计.并根据算法的外准则筛选出第二层的输入变量,重复上述步骤,依次产成第二层的中间模型z1,z2,…,z6,在外准则达到最优时,停止建模并得到最优模型y.
由于SIVIA算法在进行参数估计的过程中,采用二分对先验搜索域(priori search set)进行递归地搜索,这会使算法的计算量成指数级增加,从而耗费大量的时间和内存,甚至会使二分陷入死锁.为此,本文的算法中首先对其进行了改进,通过引入收缩算子,在解集保持不变的情况下对估计参数的搜索域进行压缩,从而减少计算的时间复杂度和空间复杂度(子块pavings中box的数量),提高算法的速度和效率.
3.1 SIVIA算法及其改进
3.1.1 SIVIA算法
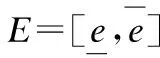
(1)
公式(1)中的y(xi)表示输入xi的观测值,ym(p,xi)为输入xi的理论输出.由式子可以看出随着样本容量的增多,S包含的范围将逐步缩小,参数集S的长度也就越小,当样本容量足够多时,待估参数的可行值越接近系统模型的真实参数.由于f是多参数非线性函数时,式(1)表示的S不能准确的计算出来,所以通过f的反函数f-1转化为式(2)的集合反演问题来进行求解.
S=f-1(Y)∩P
(2)
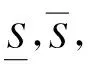
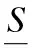
(3)
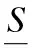
3.1.2 改进的SIVIA算法cSIVIA
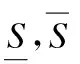

图2 改进的SIVIA算法cSIVIA
Fig.2 Improved SIVIA algorithm cSIVIA
3.2 iGMDH算法
在UBB(unknow-but-bounded)[18]假设下,iGMDH算法在对系统模型进行参数估计时,只需知道待估参数取值的范围,不需要其他人为的假设,这在一定程度上避免了人的主观因素对参数估计结果的影响.与GMDH算法相比,iGMDH算法能够将GMDH算法的输入及模型计算转变成区间数和区间运算,并把系统模型的参数估计看成是集合反演问题,应用cSIVIA算法求得待估参数近似但可靠的估计集,从而很好地解决浮点运算所产生的误差及误差累积问题.经过进一步计算,还可以得到待估参数的点估计.并且,即使在只有少量输入数据的情况下也可以进行参数的估计,且随着数据量的增多,提供的信息越丰富,估计的精度也就越高.
若系统有m个输入x1,x2,…,xm,y为该系统的输出.则给定一组输入值就必有一y值与之对应.假定有N组x的值及对应的输出y,则iGMDH算法建立系统模型的流程如图3所示.图3为iGMDH算法的伪代码,算法第1步首先对数据集进行了处理,通过提取反映系统本质的特征属性m,确定系统输入变量—输出变量的样本集合N,并将其分为训练集Nt和测试集Nc,其中,Nt≥Nc且Nt∪Nc=N,Nt∩Nc=φ.其次,通过2~3步构造K-G多项式,如公式(4)所示.
(4)
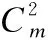
(5)
重复进行上述步骤,依次产生第二层、第三层的中间模型,如果新一层的Rmin不再减小时,则建模停止,并得到系统的最终模型(最优复杂度模型).

图3 iGMDH算法
Fig.3 iGMDH algorithm
4 实验结果与分析
4.1 实验数据
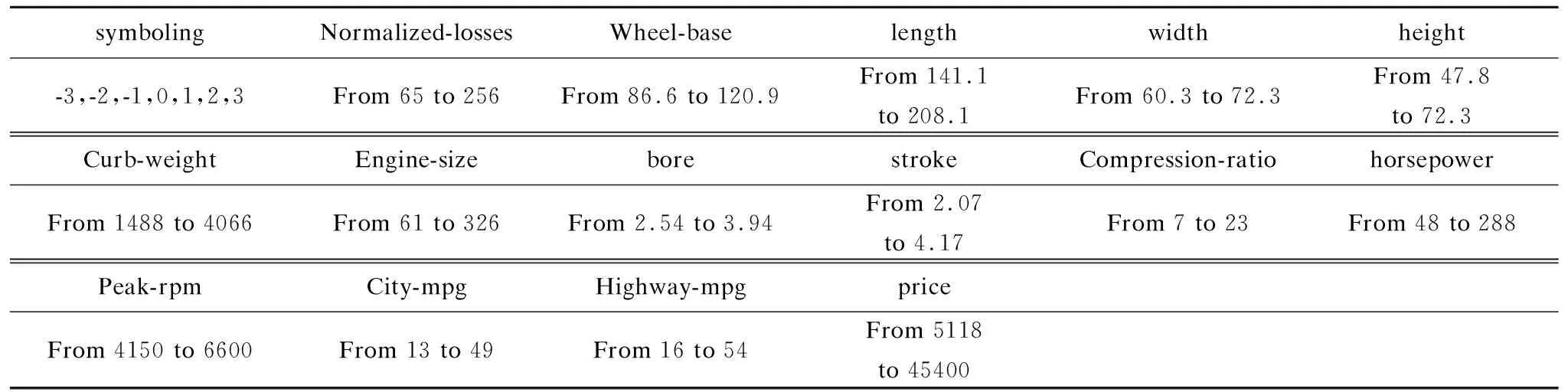
实验选用文献[9]中的数据集,该数据集由加州大学欧文分校(UCI)在实际运行环境下测得,表1给出了数据集的一些相关属性.表1所述的数据集中有在各种特征条件下汽车的自动规约值、风险等级和与指定的其他汽车相比其归一化的损耗值.在开始测试各数据之前会根据汽车的价格为每一种类型初始化分配一个安全等级,如果该汽车测试得出其安全性能降低(升高),则相应的增大(减小)其对应的风险等级,+3便是汽车的安全性能最低,-3表示其安全系数最高.实际上,原始数据集包含26个属性,但由于其中的10条对进行分析的对象(安全系数)的影响系数较低,因此可以忽略不计,直接剔除.在实验的过程中,将风险等级设为输出变量,其他15个属性作为输入变量来构建系统的连续模型.本文进行的所有实验都是在对数据进行归一化处理后进行的.
4.2 参数估计性能实验
实验对以汽车的“归一化损耗”为输出变量,“轮距”和“车速”为输入变量建立的模型分别运用cSIVIA算法和SIVIA算法对模型的参数进行了估计.本实验中,实际观测数据与模型输出间的误差E为[-1.0,1.0],先验搜索域为[-10,10]×[-10,10]×[-10,10]×[-10,10]×[-10,10]×[-10,10],容差参数ε0为0.01,不动点fp为0.001.实验主要对两种算法的计算时间和计算过程中子块pavings产生的盒子数量进行了对比.从表2中看出本文提出的cSIVIA算法在时间和产生的盒子数量上要少于SIVIA算法.
表1 实验数据集的属性
Table 1 Properties of experimental data sets
symbolingNormalized-lossesWheel-baselengthwidthheight-3,-2,-1,0,1,2,3From 65 to 256From 86.6 to 120.9From 141.1to 208.1From 60.3 to 72.3From 47.8to 72.3Curb-weightEngine-sizeborestrokeCompression-ratiohorsepowerFrom 1488 to 4066From 61 to 326From 2.54 to 3.94From 2.07to 4.17From 7 to 23From 48 to 288Peak-rpmCity-mpgHighway-mpgpriceFrom 4150 to 6600From 13 to 49From 16 to 54From 5118to 45400
表2 两种算法的比较
Table 2 Comparison of two algorithms

算法 计算时间产生的盒子数(boxes)SIVIA136S212381cSIVIA105S168175
4.3 CPS建模实验
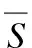

图4 模型参数的估计结果Fig.4 Estimation results of model parameters
y=[-0.030218,-0.027986]+[0.696037,0.7098921]u1
(6)
u1=[-0.065031,-0.064567]+[0.3891221,0.3902663]x1
(7)
u2=[-0.501329,-0.479862]+[-0.682412,-0.647312]x2
(8)
4.4 建模误差实验
为了验证iGMDH算法的优越性,本文做了两组对比实验,一组是不含随机噪声的实验,另一组是向实验数据集中加入随机噪声的实验,分别用两组实验来说明在数据不精确性和数据不确定性的情况下,运用GMDH算法和iGMDH算法建模时的具体对比状况.
4.4.1 不含随机噪声的情况
本文选用平均相对误差作为模型误差来评估参数估值偏离真值的程度,图5和图6分别为iGMDH算法与GMDH算法建立模型的最小均方根值及模型误差结果对比图.由图5和图6可知,iGMDH算法建模产生的最小均方根值与模型误差均比GMDH算法的小,两种算法的误差及最小均方根值的变化趋势都呈现出先减小而后增大的趋势.这是由于在建立前两层模型时误差产生的累积作用较小,而算法本身具有的收敛性,能够在误差达到最小的情况下,选出系统的最优模型.但在建立的分层模型中,即使模型误差再小也具有一定的误差累积作用,并且随着模型层数的增多,所产生误差的累积作用就会越大,从而影响模型的精确度.而iGMDH算法则不存在这个问题,它能够将取值不精确的浮点数存储为区间,基于区间进行计算.因此,应用其建立的模型要比GMDH算法所建的模型更加精确、可靠.
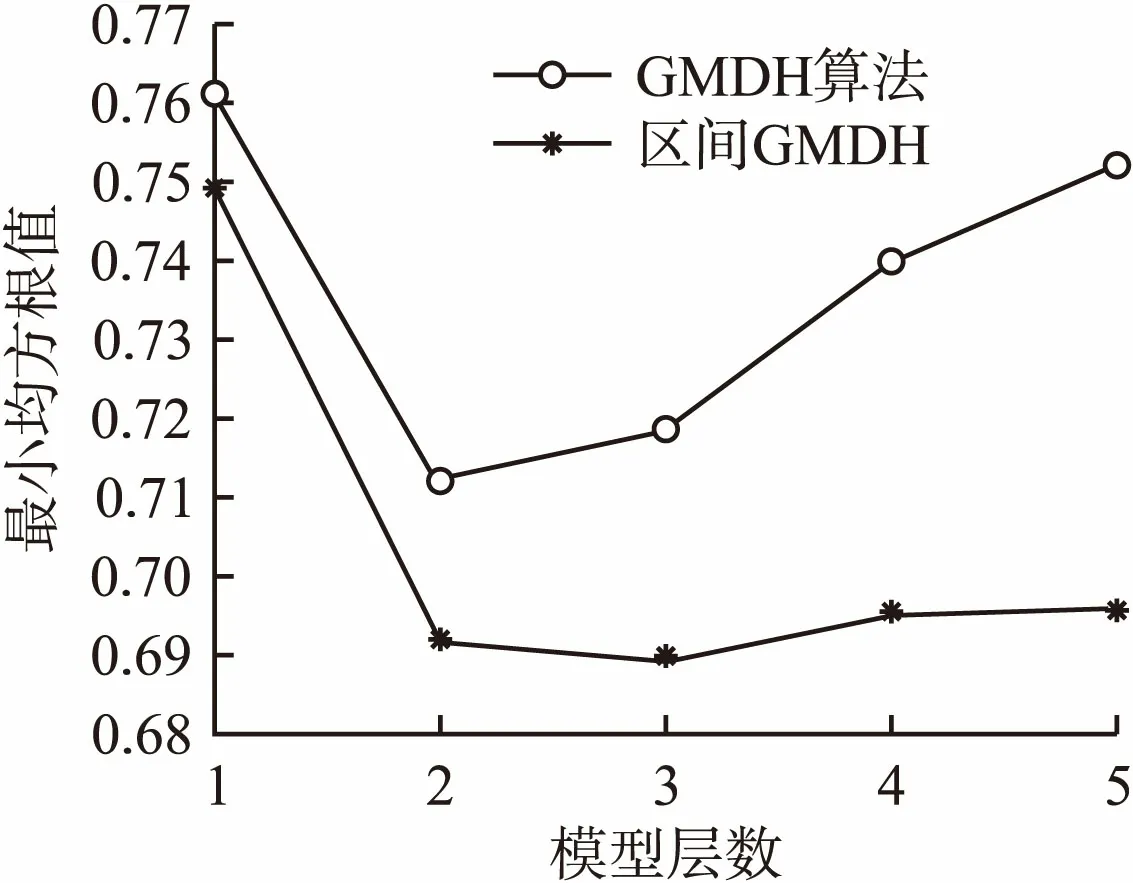
图5 最小均方根值比较Fig.5 Comparison of the minimum RMS
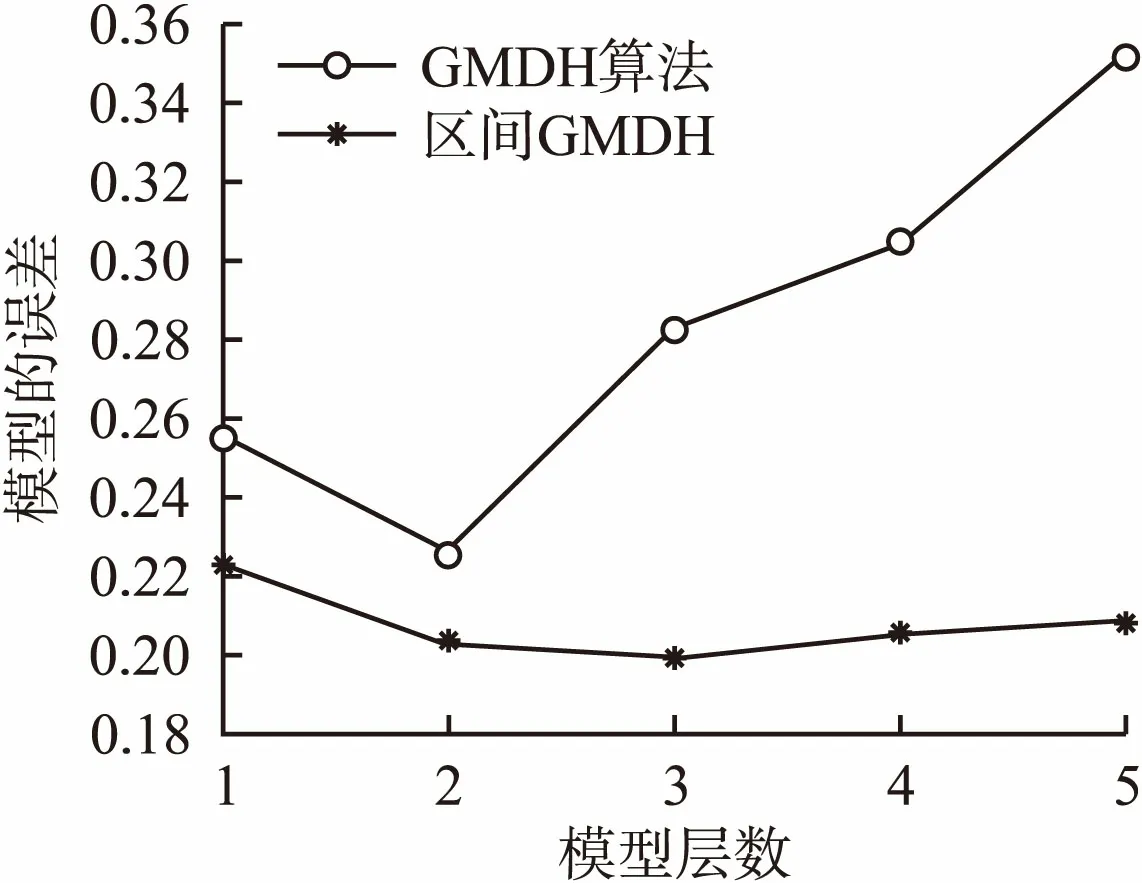
图6 模型误差的比较Fig.6 Comparison of model errors
4.4.2 含有随机噪声的情况
我们向实验数据集中加入均值为0,标准差为0.1的正态随机噪声.实验将不含随机噪声的实测数据求得的归一化损耗值作为“真实值”.将含有随机噪声的实测数据求得的归一化损耗值作为“实测值”,这样做能够保证参数估计的所有误差仅来源于样本数据及参数估计的方法本身,以便于研究随机噪声对模型参数估计结果的影响.表3为在实验数据不含随机噪声和含有随机噪声的情况下,iGMDH算法与文献[12]中GMDH算法选择相同变量建立模型的参数估计结果.由表3可以看出在有随机噪声干扰的情况下,GMDH算法参数估计结果明显偏离了参数的真实值,而iGMDH算法无论是在有噪声干扰的情况下还是无噪声干扰的情况下,都能稳健地得到可靠的逼近真实值的解集.进一步计算求得区间参数的点估计,通过计算模型的相对误差来评估参数估计值偏离其真值的程度,即参数的估计精度.求得iGMDH的平均相对误差为1.56363%,GMDH算法的为3.40609%,由此可以得出,iGMDH算法估计精度、抗噪性均优于GMDH算法.
表3 实验数据有噪声、无噪声情况下两种算法参数估计结果对比
Table 3 Comparison of parameters estimation results between two algorithms with or without noise in experimental data
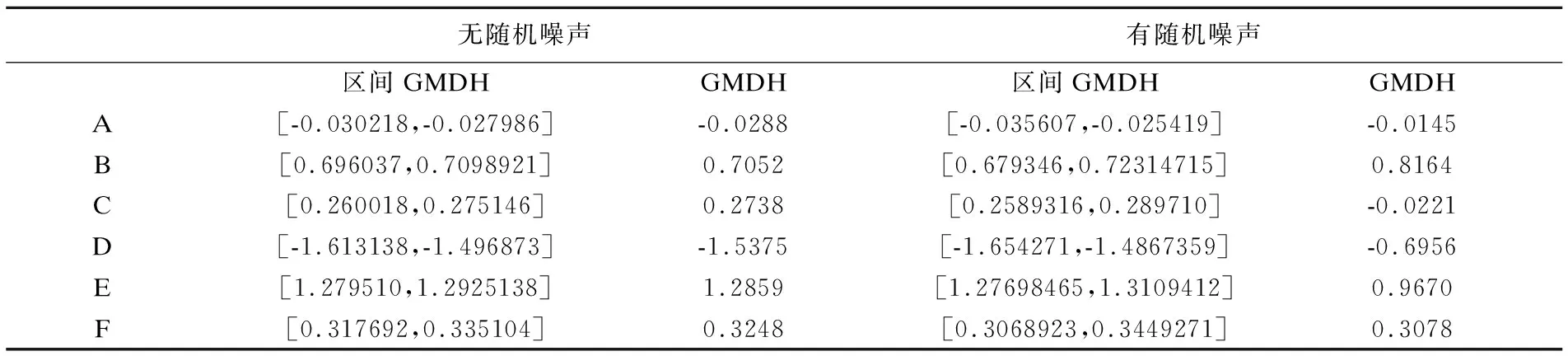
无随机噪声有随机噪声区间GMDHGMDH 区间GMDHGMDH A [-0.030218,-0.027986]-0.0288 [-0.035607,-0.025419]-0.0145 B [0.696037,0.7098921]0.7052 [0.679346,0.72314715]0.8164 C[0.260018,0.275146]0.2738 [0.2589316,0.289710]-0.0221 D [-1.613138,-1.496873]-1.5375 [-1.654271,-1.4867359]-0.6956 E [1.279510,1.2925138]1.2859 [1.27698465,1.3109412]0.9670 F[0.317692,0.335104]0.3248 [0.3068923,0.3449271]0.3078
5 结 语
为了解决CPS系统建模过程中由于数据不精确性以及随机噪声引起的数据不确定性产生的误差及误差累积问题,本文将GMDH算法用区间分析的算法加以改进,首先通过引入收缩算子,对估计参数的搜索域进行压缩,改进了SIVIA算法,提出了cSIVIA算法.其次,将GMDH算法的输入和计算转变为区间数和区间计算,利用cSIVIA算法进行模型的参数估计,从而提出新的算法—iGMDH算法,建立了具有区间参数的模型.实验结果表明本文提出的iGMDH算法能够使估计得到的区间参数直接包含在计算之中,在有无噪声干扰的情况下都能够得到待估参数近似但可靠的估计集.与GMDH算法相比,算法的精确度高、抗噪性强,有效地解决了建模过程中存在的误差及误差累积问题,为我们更加准确地估计和评价所得结果提供了新的依据.此外,该算法在样本容量较少的情况下也能够求得模型参数的近似估计,这对于CPS系统的研究与应用具有重要意义.

