高效非结构网格变形与流场插值方法

郭中州，何志强，赵文文，陈伟芳

浙江大学 航空航天学院，杭州 310027

含有动边界的非定常流动问题在航空航天领域十分常见，如火箭的级间分离、飞行器的机动、外挂物投放等。这类问题通常伴随着复杂的气动干扰和强烈的非定常效应。对这类非定常流动问题的精确和高效模拟已经成为了当前计算流体力学(Computational Fluid Dynamics, CFD)和航空航天领域的研究热点之一。在此基础上发展的“数值虚拟飞行”技术，更是被称为航空领域CFD应用的最后一个大挑战[1]。

动网格方法由于计算效率高，适合处理边界变形问题等特点，成为解决此类问题的一种重要方法，得到了广泛的关注。国外从20世纪八九十年代就开展了利用动网格技术求解动边界问题的研究，Batina[2]首先使用弹簧动网格模拟了NACA0012翼型的俯仰运动。Cavallo等[3]采用非结构动网格以及网格自适应技术模拟了外挂物投放和火箭级间分离。但在模拟过程中进行网格调整时需要进行人工干预。Panagiotopoulos和Kyparissis[4]采用非结构动网格和欧拉方程，模拟了外挂物投放，并与试验结果进行了对比。Luo和Baysal[5]模拟了高超声速飞行器从助推器上的分离过程。Bartels[6]模拟了带有扰流板的机翼的气动弹性问题。Baum等[7]研究了F16C/D战斗机抛掷油箱的动态过程，并得到了与风洞试验和飞行数据吻合良好的结果。

在国内，刘君等[8]采用非结构动网格方法和欧拉方程，对飞行器的配平迎角计算、多体分离和结构动力学等问题进行了模拟。白晓征[9]结合网格变形和网格重构并耦合多体动力学，模拟了内嵌式助推器的分离过程。陈坚强等[10]采用结构动网格技术，研究了方形弹舵面操纵下导弹的俯仰运动响应过程。张来平等[11]介绍了气动/运动/控制耦合一体化计算方法，探讨了数值虚拟飞行中的一些挑战性问题。常兴华[12]使用非结构动网格模拟了鱼体的巡游和昆虫翼的拍动。伍贻兆等[13]分别采用非结构动网格和非结构重叠网格模拟了三维外挂物投放、直升机机身+旋翼前飞以及机翼气动弹性变形等问题。王刚等[14]提出了基于贪心法逐级选择径向基函数空间子集的方法，提高了径向基函数方法计算网格变形时的效率。陈龙等[15]发展了Delaunay图映射弹簧混合动网格方法，并应用到机翼气动弹性计算中。

目前，国外成熟的商业CFD软件中大多集成了重叠网格方法或者动网格方法。如Fastran[16]采用了重叠网格方法。Fluent[17]中采用了非结构动网格方法。一些国外的开源软件，如OpenFOAM[18]，也集成了多种非结构动网格方法。由于边界运动的形态多种多样，商业软件中大多具备一定的扩展功能，如Fluent的用户自定义函数(User Defined Function, UDF)功能模块，以方便用户处理各种不同类型的动网格问题。

当边界变形导致网格质量过差时，为了改善网格质量，需要进行网格重构，造成计算效率下降。重构后的流场插值过程还会引入额外的耗散，甚至导致流场产生波动，发展高效、健壮的插值方法至关重要。Smith和Quon[19]发展了基于点云和径向基函数的重叠网格流场插值方法。Hner[20]总结了非结构网格上的插值方法的不足。Olsson和Petersson[21]研究了一维重叠网格插值的稳定性问题。王永健[22]提出了一类适用于任意网格的守恒重映方法。董海波等[23]提出了基于格点格式有限体积法的流场数据传递方法。利用非结构动网格技术，将旧网格单元移动到新网格单元，同时求解流场控制方程，以此来实现两套网格间的信息传递。徐喜华等[24]提出了一种三维非结构多面体二阶保界全局重映算法，在旧网格上选取模板利用最小二乘构造插值多项式，采用凸包算法计算多面体相交，最后使用局部保界修正技术修补重映后的越界量。

网格变形、网格重构以及流场插值方法是非结构动网格的核心技术。此方面的研究仍在不断发展之中。本文基于KD(K-Dimension)树数据结构，提出了高效的网格变形方法和流场插值方法以及相应的并行化方法。发展了灵活设置边界运动的UDF功能，并通过几个算例的模拟对方法进行了验证。

1 高效网格变形方法

弹簧近似方法[2，25-26]和径向基函数(Radial Basis Functions, RBF)方法[27-30]是目前应用最为广泛的两类非结构网格变形方法，弹簧近似方法的物理意义清晰，实现简单，但是变形能力较弱，只能处理较小幅度的网格变形。相比之下，RBF方法具有变形能力强，不受网格拓扑限制等优点。但是原始的RBF方法需要求解大型线性方程组，方程组的阶数与动边界的节点数目相同，当动边界上的网格较密时，求解方程组的计算量很大。导致计算效率下降。

此外，RBF方法需要指定支撑半径，网格的变形都局限在支撑半径之内，无法传递到更远的网格区域。对于动边界与固定边界相距较近的问题，难以选取合适的支撑半径，因而需要频繁进行网格重构，影响计算精度和计算效率。

1.1 KNN-RBF网格变形方法

为了高效地处理非结构网格的大变形问题，提出了K近邻-径向基函数(K Nearest Neighbor-Radial Basis Functions, KNN-RBF)网格变形方法。在计算网格变形时，首先分别查找网格点到动边界的K个最近点及到其余边界的K个最近点，然后通过式(1)计算网格点的位移。

(1)

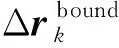
式(1)中K的值可根据计算效率和网格来选取，代表了动边界上对网格点的位移有影响的区域范围，通常取K≤10即可。选取较大的K值时，表明网格点位移由动边界上多个最近点的位移决定，可以更好地将动边界的位移传递到网格点处，但计算量也会相应增大。对动边界上网格较密或者外形较为简单的算例，取K=1即可。

径向基函数的形式多种多样，本文采用了在网格变形中广泛应用的Wendland C2[31]型基函数。其形式为

(2)

可以看出，KNN-RBF与其他RBF方法有较大区别：① KNN-RBF方法不需要设置支撑半径。② RBF方法需要通过求解线性方程组来得到边界点的权值，再根据权值计算网格点的位移。而KNN-RBF方法只需要进行K近邻查找。K近邻的查找采用KD树[32]实现。KD树是一种平衡二叉树，如图1所示，它将多维数据按照各个维度进行分割，然后形成一棵平衡二叉树。利用二叉树实现邻近数据的快速查找。

设网格总的节点数目为M，动边界的节点数目为N，固定边界的节点数目也为O(N)量级。使用KNN-RBF方法计算网格变形时，每个网格点需要查找2K个邻近点。将动边界节点构建成KD树，利用KD树查找一个邻近点的平均时间复杂度为O(lbN)。则查找所有网格节点邻近点的平均时间复杂度为O(2KM(lbN))，网格变形过程的时间复杂度为O(KM)。而RBF方法需要求解3个线性方程组，采用直接求解法，总时间复杂度为O(3N3)，网格变形过程的时间复杂度为O(MN)。对于网格总的节点数目和边界节点数目的关系，可认为O(M)=O(N1.5)。则KNN-RBF方法总时间复杂度为O(2KN1.5(lbN))，RBF方法总的时间复杂度为O(3N3)。

可以看出，RBF方法的主要瓶颈在于求解线性方程组。相比于RBF方法，KNN-RBF方法解决了支撑半径的选取问题，同时大大提高了网格变形过程的计算效率。

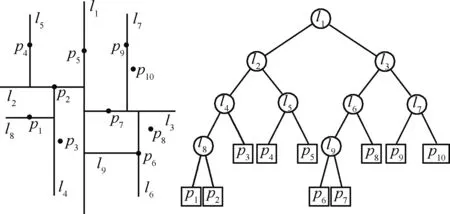
图1 KD树的数据结构Fig.1 Data structure of KD tree

1.2 网格变形的并行化方法

为了适应复杂外形的计算精度和效率的要求，使用消息传递接口[33](Message Passing Interface, MPI)技术在程序中实现了KNN-RBF方法的并行化。

在计算之前，首先使用多级K路图算法[34]对网格进行分区，将原始网格分成多个数目均衡的网格块，实现并行计算时各进程的负载平衡。

网格变形的每一步都需要使网格的分区边界上对应点的坐标在变形前后保持一致，避免变形后出现网格重叠或撕裂。这是网格变形方法并行化的关键步骤。基于红黑树[35]数据结构，设计了交界面节点的一致性方法。

读入网格后，为每个网格点设置一个唯一的全局编号，记为Uuid。进行网格分区时，交界面上的节点被分到了不同的网格块中，如图2所示。再为每个节点设置一个局部的编号，这样，相邻网格块的分区边界上的对应节点具有相同的全局编号。在读入各个分区的网格时，建立分区对接点局部编号和全局编号之间的映射关系并采用红黑树存储。可以快速高效地查找局部编号和全局编号的对应关系。

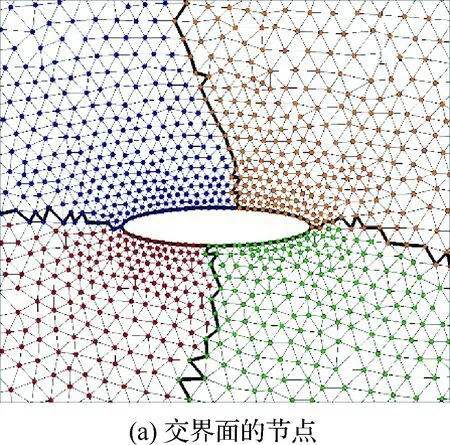
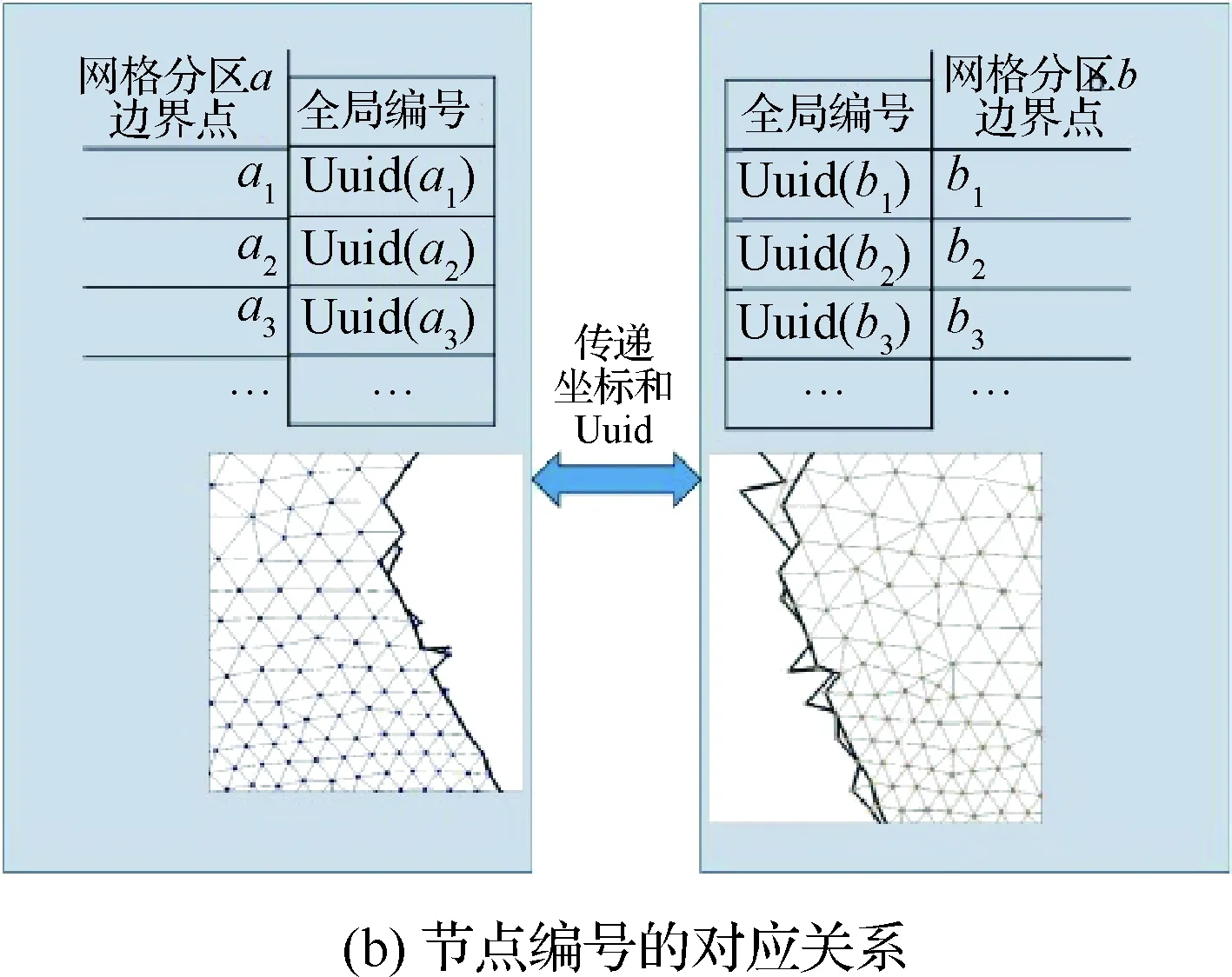
图2 交界面上对接节点的对应关系Fig.2 Corresponding relationships of patch nodes on zonal boundaries

在进行网格变形时，首先分别对各个网格块采用网格变形方法计算各自网格点的位移，然后各进程进行通信，各相邻的网格块互相传递交界面上的对接点的全局编号和变形之后的新坐标值。各分区根据接收的节点全局编号找到在本分区的对应点，将接收的节点坐标与本分区对应点的坐标进行加权平均，作为交界面上点的新坐标。这样就保证了分区交界面上网格点坐标的一致性。

基于上述的交界面节点一致性方法，实现了弹簧近似方法[2]、贪婪RBF方法[28]和KNN-RBF等多种网格变形方法的并行化。对于弹簧近似方法，并行策略为先计算各分区的网格点位移，然后设置交界面节点位移。对于RBF方法和KNN-RBF方法，需要各进程先收集所有边界点，然后再计算各分区网格点的位移，最后设置交界面节点的位移。

2 边界运动的UDF功能实现

对含有动边界的非定常流动问题，流场中可能有多个运动物体，如图3所示，每个物体又由多个部件组成。例如多体分离、子母弹抛撒等问题，且不同物体可能以不同的规律运动，如变形、强迫运动以及六自由度运动等等。为了能够灵活设置边界的运动，在自主发展的非结构混合网格程序GUO-CFD (General Unstructured Oriented-Computational Fluid Dynamics)中实现了UDF功能，可以方便地设置动边界的各种运动。

使用UDF设置边界的运动时，首先在边界条件文件中将运动规律相同的边界划分为一个运动组，然后为每个运动组编写相应的UDF，在UDF中设置运动参数的变化规律，计算时CFD程序通过动态调用UDF来改变运动组的运动参数。

图3 运动组的定义Fig.3 Definition of motion groups

为了使CFD程序与UDF之间的数据交互通用化，采用了JSON (JavaScript Object Notation)格式的文件来描述每个运动组的运动参数。JSON是一种标准化的数据交换格式，可以灵活地表达不同边界的运动。以某个运动组的六自由度运动为例，对应的JSON格式的运动参数如图4所示。

为了方便不同情况下的使用，UDF分为了编译型UDF和解释型UDF。编译型UDF采用C++ 语言实现，在程序首次执行时将UDF文件编译为动态链接库，通过运行时加载其中的函数实现自定义的边界运动。编译之后可以在Windows和Linux平台上执行，运行速度快。可以直接设置动边界的各个运动参数，也可以通过返回JSON格式的运动参数与CFD程序进行交互。

解释型UDF采用Python语言脚本实现，可以定义动边界的质心坐标、质量、惯性矩、速度、角速度、外力及姿态角等参数的变化规律，通过返回JSON格式的运动参数与CFD程序进行交互，实现对边界运动的控制。无需编译即可在不同系统上运行。但是相比于编译型UDF功能有限，需要安装Python运行环境，且运行速度比编译型UDF慢。

图4 JSON表示的动边界运动参数Fig.4 JSON represented motion parameters of moving boundary

3 网格重构

根据重构过程涉及的网格范围，可以将重构策略分为局部重构和全局重构。

局部重构只在质量较差的网格单元附近区域重新生成网格，网格生成阶段的计算量较小。但网格生成后需要与旧网格进行合并，消除网格的复边。网格数据结构和流场变量都需要进行动态调整。过程比较复杂，只能改善局部的网格质量，通用性较差。且并行情况下分区交界面上的网格质量也可能变差，难以进行并行化处理。

相比而言，全局重构在网格生成阶段的计算量较大，但可以有效地改善整体网格质量，对网格数据的处理也比较方便，可以方便地调用网格生成接口。并且能够保持重构后并行计算的负载平衡，因此后续采用了全局网格重构的策略。在程序中实现了调用其他网格生成程序的接口，可以直接调用自编网格生成程序或者商业软件。

3.1 网格质量准则

对于四面体网格，采用单元的半径比来衡量网格质量，其表达式为

(3)

式中：Rs和rs分别为四面体外接球和内切球的半径。

对于混合网格，q的表达式为

(4)

式中：Li为单元各顶点到单元中心的距离；E为Li的平均值；Cn为单元的节点数目。

在计算时需要设置q的阈值，当网格的最差质量低于此值时则认为需要进行网格重构。

3.2 网格重构流程

按照前述的网格质量准则，每步网格变形之后，对各进程的网格进行检测，当发现网格质量较差时，进行网格重构。网格重构的步骤如下：

步骤1备份当前的计算结果，将各个进程的边界网格合并成一个整体，作为网格重构的输入。

步骤2阻塞其他进程，主进程调用面网格光顺程序，对合并后的边界网格进行调整，保证边界网格的质量。然后调用网格生成子程序或者商业软件，生成新网格并进行光顺。保证重构后的网格质量满足计算要求。

步骤3对新网格进行分区，各进程读入对应的新网格块并替换旧网格块，网格的数据结构如图5所示，需要相应更新网格的单元、节点和面元等信息，同时保持原有边界的边界条件、运动组和UDF等不变。

整个网格变形和重构过程如图6所示，重构过程中不需要人工干预。

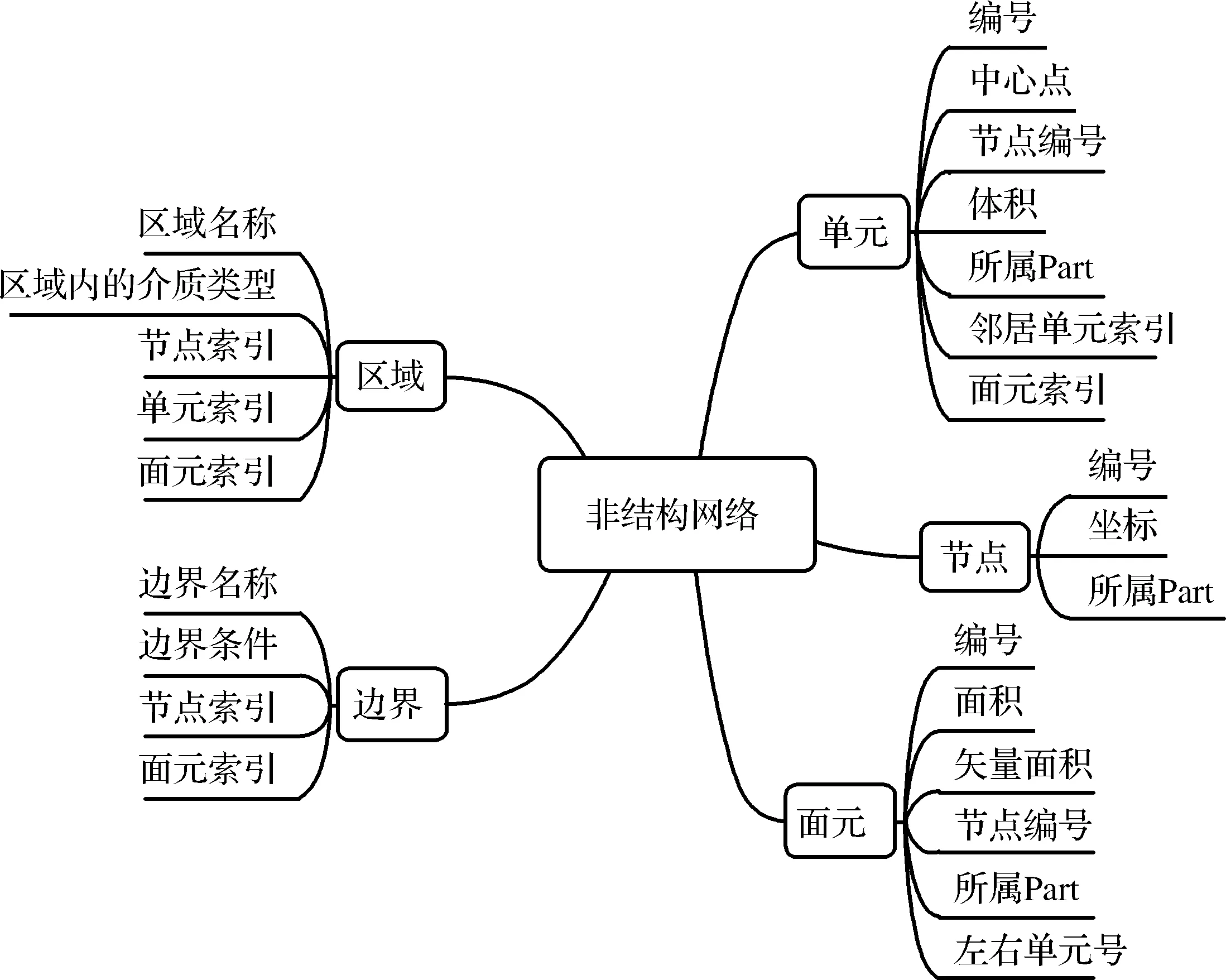
图5 非结构网格的数据结构Fig.5 Data structure of unstructured mesh

图6 网格的并行变形和重构过程Fig.6 Parallel mesh deformation and regeneration procedure

4 并行流场插值方法

重构过程完成后，还需要将旧网格上的物理量插值到新网格上。为了保持流场的守恒性，理论上应当采用守恒的插值方法，但是目前还难以构造一种高效、健壮而且通用的守恒性插值方法。目前在重叠网格和动网格插值中都广泛地采用了非守恒插值，并取得了良好效果。最常用的是线性插值，进行插值时，首先要在旧网格上寻找贡献单元，然后使用贡献单元的物理量插值得到新网格上的物理量。

新旧网格的分区通常互不重合。如图7所示，若采用顺序查找，需要在所有网格块中查找贡献单元。当网格量很大时，整个插值过程将耗时巨大。为了定位贡献单元，要进行大量的几何关系判断，如果新网格点由于误差等原因查找失败，还要进行额外处理，健壮性难以保证。

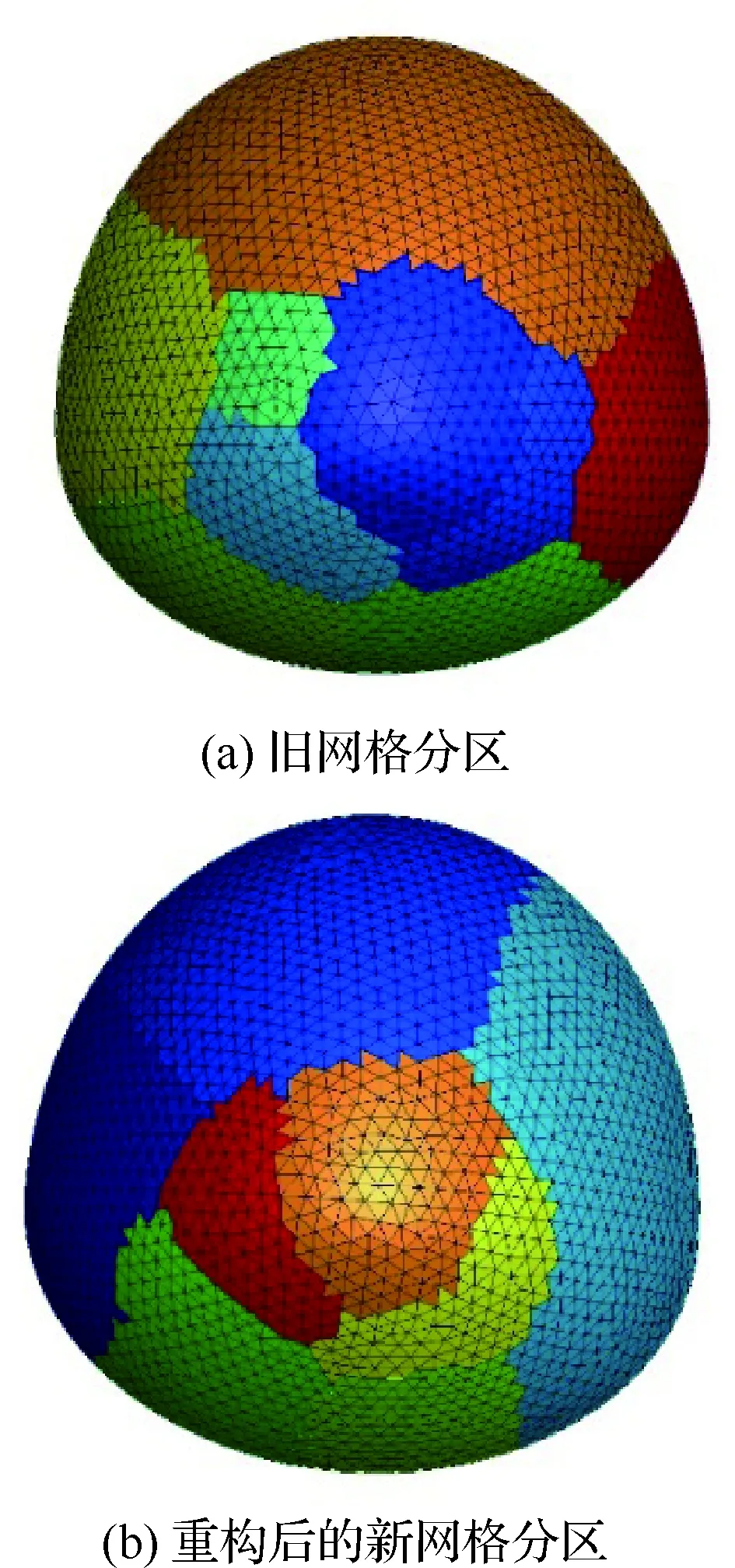
图7 旧网格和新网格的网格分区Fig.7 Mesh partitions of old mesh and regenerated mesh

4.1 两级KD树插值方法

为提高插值过程的计算效率和健壮性，基于KD树数据结构，提出了两级KD树方法，实现并行条件下对贡献单元的快速查找。方法分为以下步骤：

步骤1查找贡献单元所在的网格块。分别将旧网格各网格块的边界点构建成KD树，作为第1级KD树，在其中查找新网格单元的最近点，如果由新网格单元点指向最近点的矢量与旧网格边界在最近点的外法向的点积为正，则认为贡献单元位于此网格块内。在靠近分区界面处，如果网格较为扭曲，可能有不止一个网格块满足条件，则认为贡献单元位于多个网格块内。

步骤2在对应的网格块中定位贡献单元。将旧网格各个网格块的单元中心点分别构建成KD树，作为第2级KD树，在定位了新网格的点位于旧网格的哪个分区之后，再利用这个分区的单元点的KD树，得到新网格点在旧网格上的邻近点，即为插值的贡献单元。

步骤3使用贡献单元的物理量进行插值。采用线性插值公式，根据邻近点的空间位置关系将物理量插值到新网格点。

由于最近点必然存在，因此两级KD树插值方法的健壮性可以得到保证，其本质上也属于线性插值，具有一阶精度。由于线性插值是基于泰勒展开，到插值点的距离越近，插值引起的耗散越小，而两级KD树方法使用的是最近点进行插值，因此相比其他线性插值方法具有更小的数值耗散。

4.2 时间复杂度分析

假设并行计算时有Np个网格块，每个网格块的单元数目为Nc，每个网格块的边界网格点数目为Nb，且新旧网格的单元数目为同一量级。如果采用线性查找，需要依次遍历各个分区的网格以定位贡献单元。定位一个贡献单元的平均时间复杂度为O(NpNc)。

对于两级KD树方法，每个网格块的边界点都构成一棵平衡二叉树，在每棵树中查找的平均时间复杂度为O(lbNb)，则查找贡献单元所属旧网格块的平均时间复杂度为O(Np(lbNb))，在旧网格块中查找贡献单元的时间复杂度为O(lbNc)。整个过程总的时间复杂度为O(Np(lbNb)+lbNc)。通常情况下，有Np≪Nb≪Nc，则定位一个贡献单元总的时间复杂度为O(lbNc)。因此，与线性查找相比，两级KD树方法具有更高的效率。

5 算例验证

5.1 标量函数插值

采用了两套非结构网格。网格A为六面体单元，网格B为混合网格。函数的表达式为z=x2+y2，先根据函数直接得到网格格心处的函数值。然后插值到另外一个网格上，分别计算了由网格A插值到网格B和由网格B插值到网格A两个算例，得到的截面上的插值误差分布如图8所示。最大插值误差均在5%之内，表明插值方法具有较高精度。

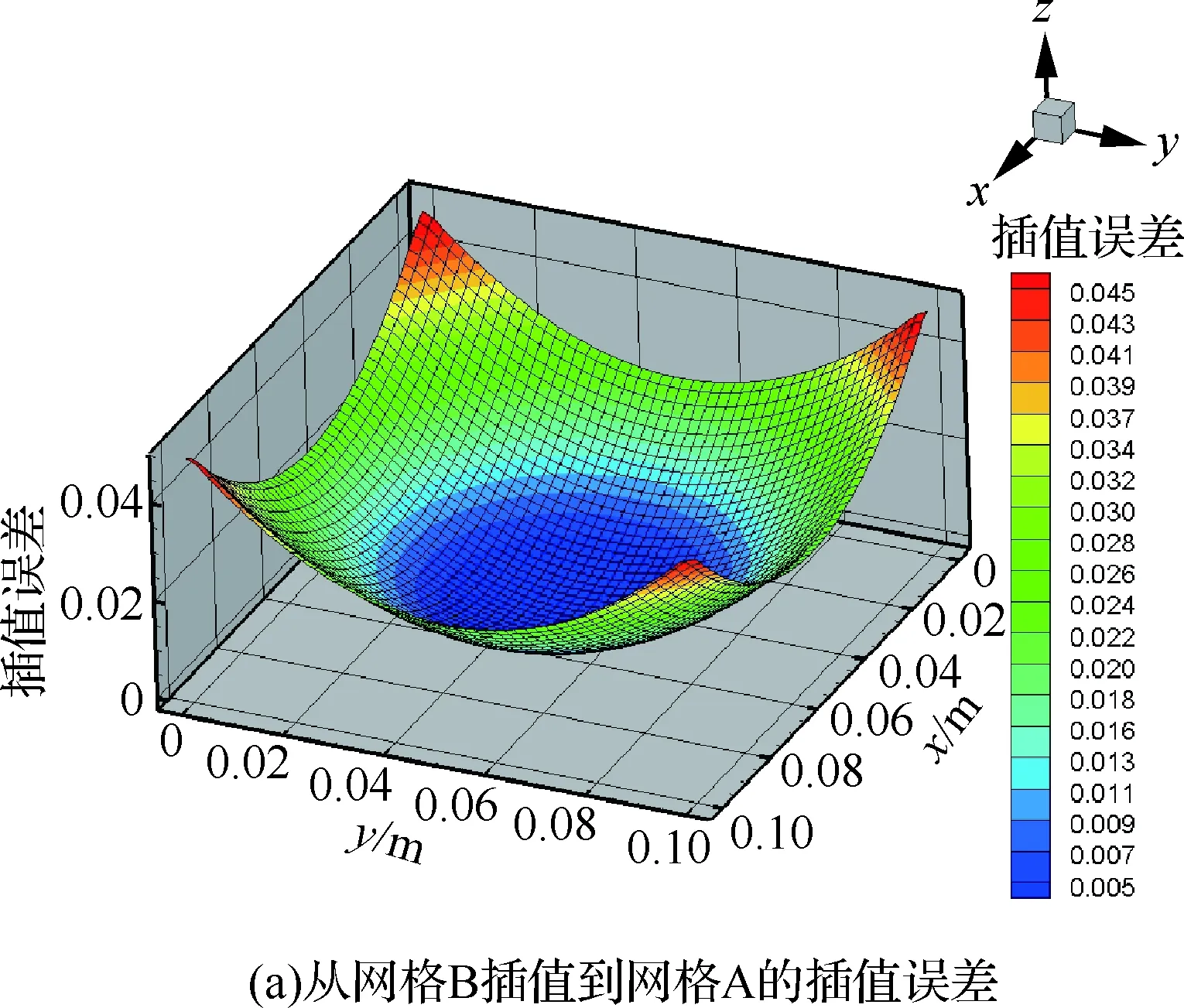
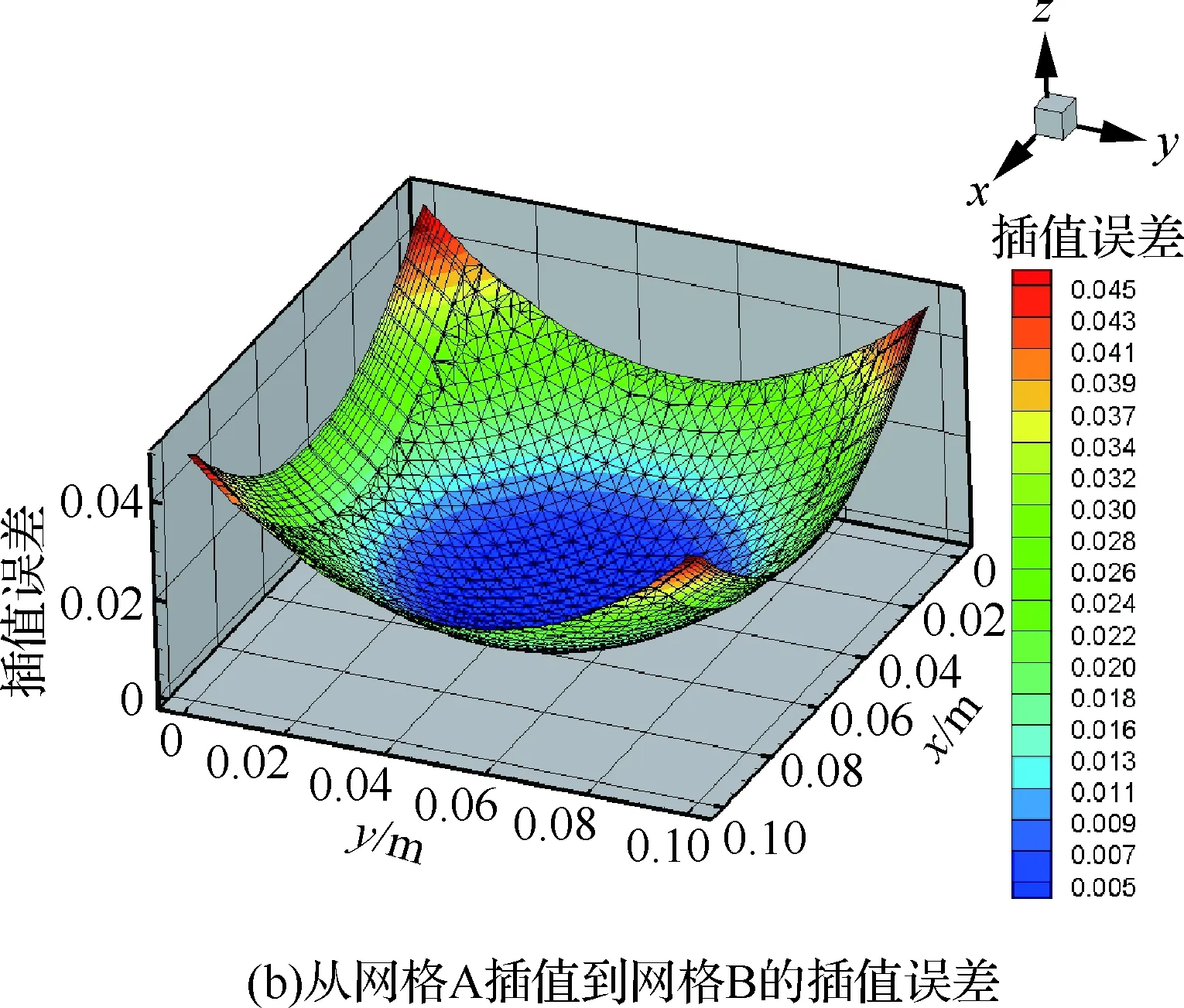
图8 给定函数在非结构网格上的插值误差Fig.8 Interpolation errors of given function on unstructured meshes

5.2 NACA0012翼型流场插值

采用前述的并行流场插值方法，对NACA0012翼型的定常流场插值进行了验证。计算采用的两套网格如图9所示。

计算状态对应的来流马赫数为0.755，迎角为2.526°。首先采用六面体网格计算出流场结果，然后将计算结果插值到非结构网格上，得到的压力等值线如图10所示。图10中的粗线为截面与网格块边界的交线。可以看出，插值前后流场的压力等值线云图一致性符合较好，验证了插值方法的有效性。

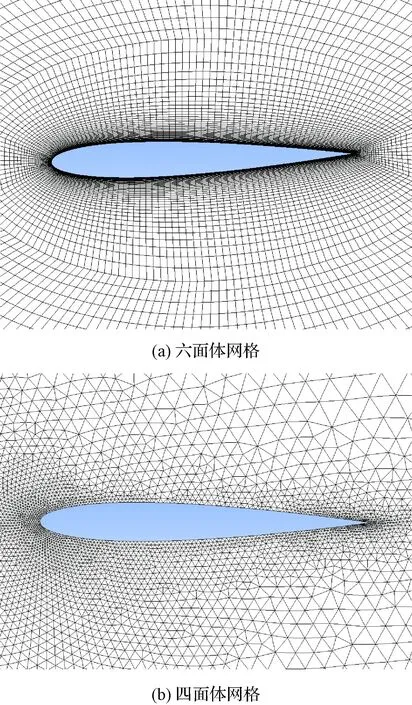
图9 插值采用的六面体网格和四面体网格Fig.9 Hexahedron and tetrahedron meshes used for interpolation

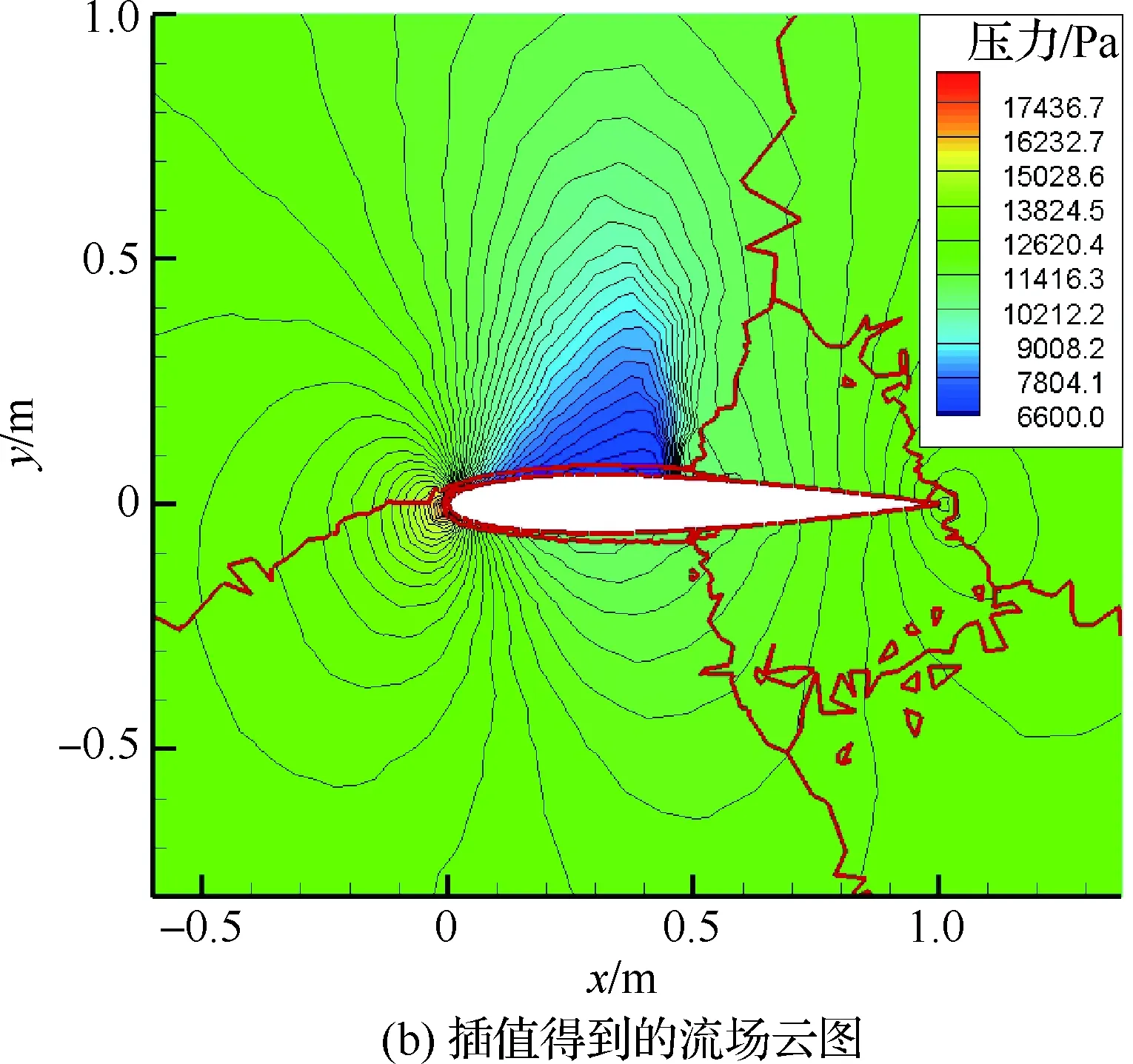
图10 原始结果和插值得到的压力云图对比Fig.10 Comparison of pressure contours of original and interpolated results

5.3 外挂物投放模拟

算例外形为具有详细试验数据的Wing/Pylon/Finned store外形[36]，该算例被广泛用于验证动网格和重叠网格程序的正确性。采用的网格为四面体网格，单元数目约156万，在挂架和外挂物之间的缝隙等细节位置对网格进行了加密，表面网格的分布如图11所示。

采用有限体积法求解ALE(Arbitrary Lagrangian-Euler)形式的控制方程，其中，梯度采用加权最小二乘法计算，对流通量格式采用考虑网格运动速度的Van Leer格式，限制器采用Venkatakrishnan限制函数。为提高计算效率，采用32个 计算核心并行计算。首先模拟了高度为10 km，马赫数为1.2的定常流场作为初场。然后使用双时间步长方法模拟了外挂物投放后0.8 s内的非定常流场。不同时刻外挂物位置如图12所示。

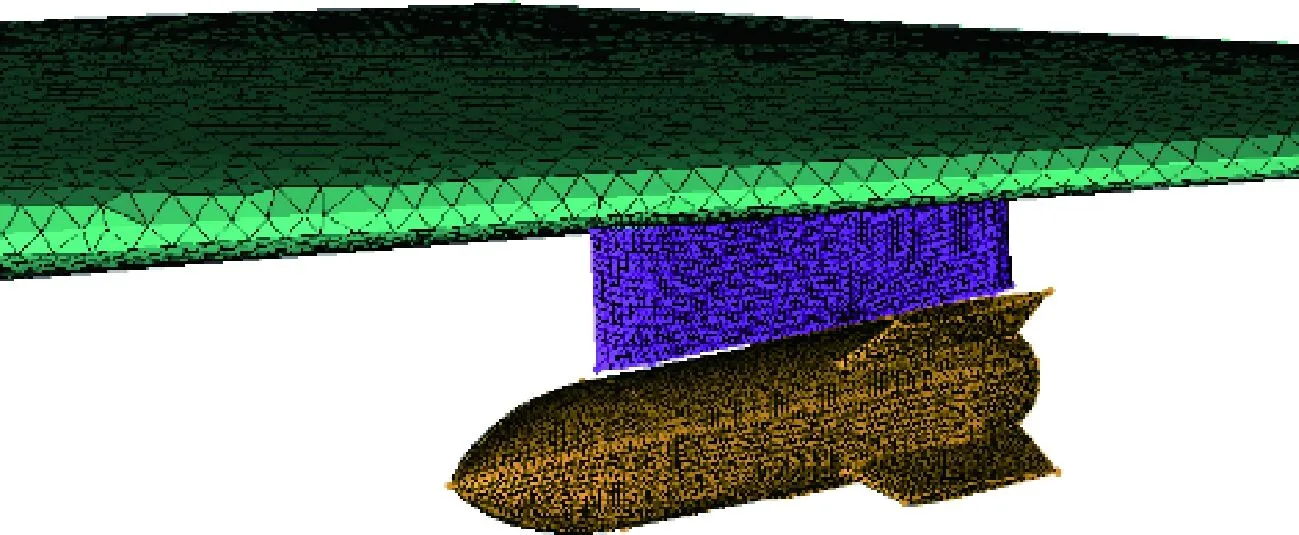
图11 Wing/Pylon/Finned store外形Fig.11 Configuration of Wing/Pylon/Finned store

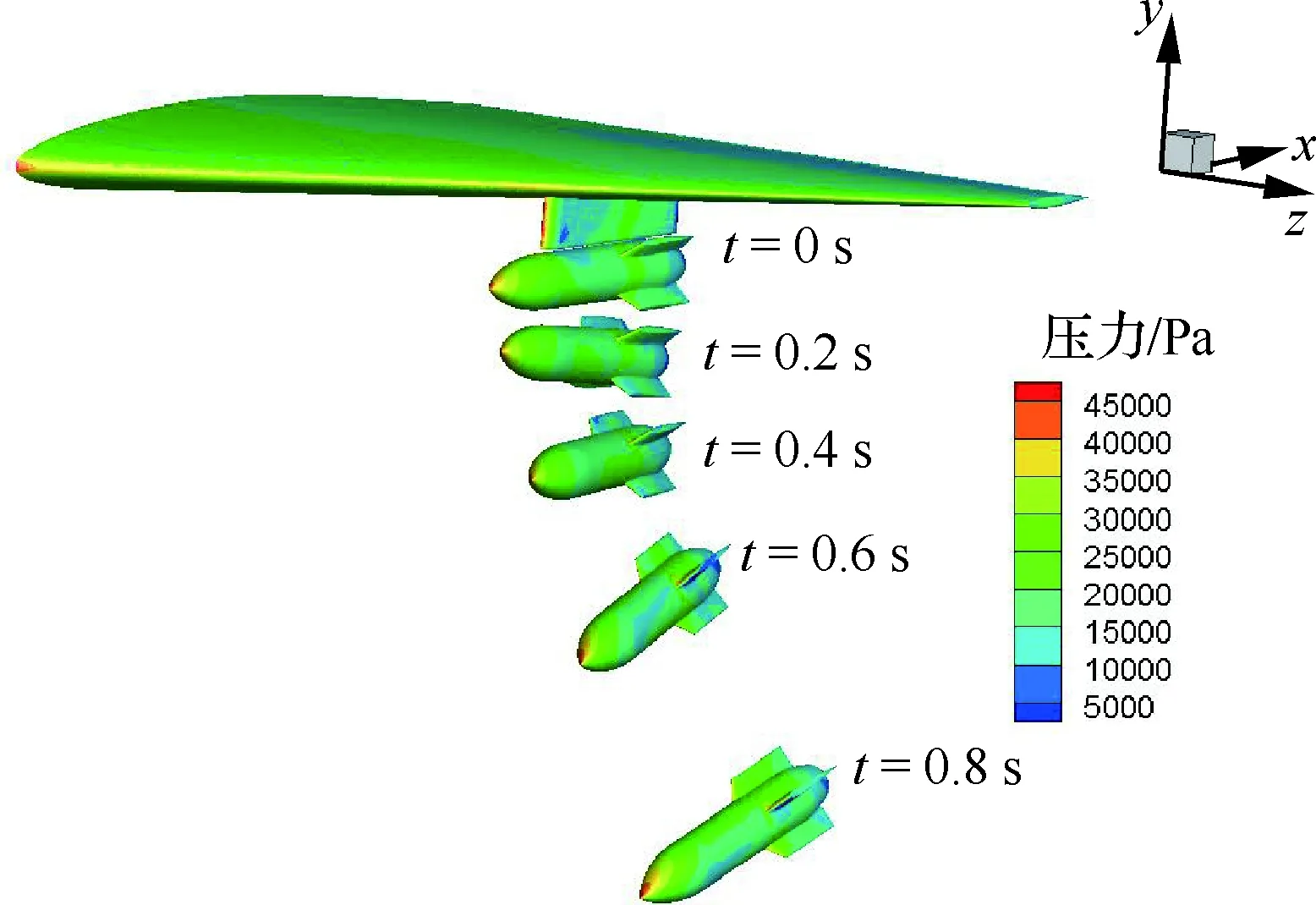
图12 不同时刻外挂物的位置Fig.12 Position of external store at different interval times

分别采用弹簧近似方法、贪婪RBF方法和KNN-RBF方法进行了计算。其中，弹簧近似方法的迭代次数为50次，贪婪RBF方法的插值误差取10-5m，支撑半径为1 m，KNN-RBF方法取K=1，3种方法的最差网格质量阈值均取qmin=0.001。

在整个过程中，弹簧近似方法进行了15次重构，贪婪RBF方法进行了11次重构，KNN-RBF方法进行了4次网格重构。

图13为KNN-RBF方法重构前后的网格对比，可以看出，随着外挂物的下落，挂架和外挂物之间的网格被不断拉长，质量明显变差，但紧贴物面处的网格质量保持较好。重构之后，中间区域的网格分布得到改善。

为了考察3种方法的计算效率，统计了计算过程中各进程的动网格模块占用的CPU时间的平均值。以KNN-RBF方法的平均CPU时间为基准，用无量纲CPU时间来衡量3种方法的计算效率，结果如图14所示。对本算例而言，只考虑网格变形子程序占用的时间时，弹簧近似方法的效率最高。KNN-RBF方法和贪婪RBF方法都需要收集各网格块的边界点，故并行计算效率比弹簧方法低。而计入网格重构和流场插值占用的时间后，由于KNN-RBF方法变形能力强，所需重构次数少，相比其他两种方法具有明显优势。同时可看出网格重构和流场插值会对计算效率产生重要影响。

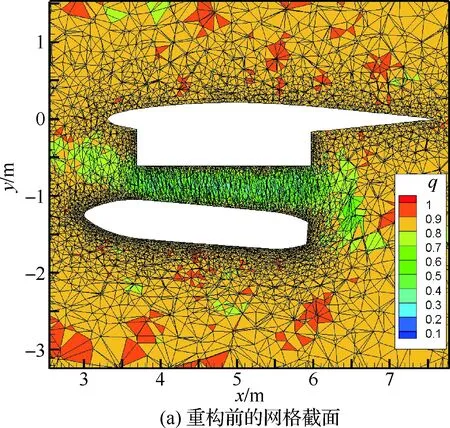
图13 重构前后的网格分布对比Fig.13 Comparison of mesh distribution before and after regeneration

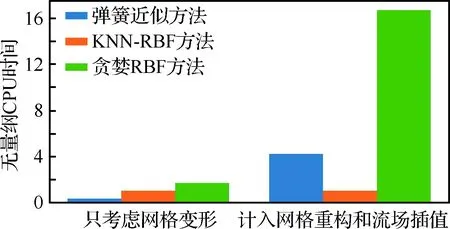
图14 3种方法的CPU时间比较Fig.14 Comparison of CPU time of three methods

图15展示了外挂物质心、欧拉角的计算值与试验值的对比。偏航角在整个过程中与试验值都吻合较好，俯仰角在0.6 s之前符合较好，之后偏差逐渐增大。而滚转角在0.4 s之后偏差逐渐增大，由于外挂物滚转惯性矩的量级较小，对气动力矩的误差十分敏感，再加上计算时未考虑黏性影响，故其计算值和试验值差异较大。质心位移在整个过程中符合较好，但后期也出现偏差增大的趋势。总体而言，随着计算时间的增加，上述6个运动参数的偏差都有不断增大的趋势。

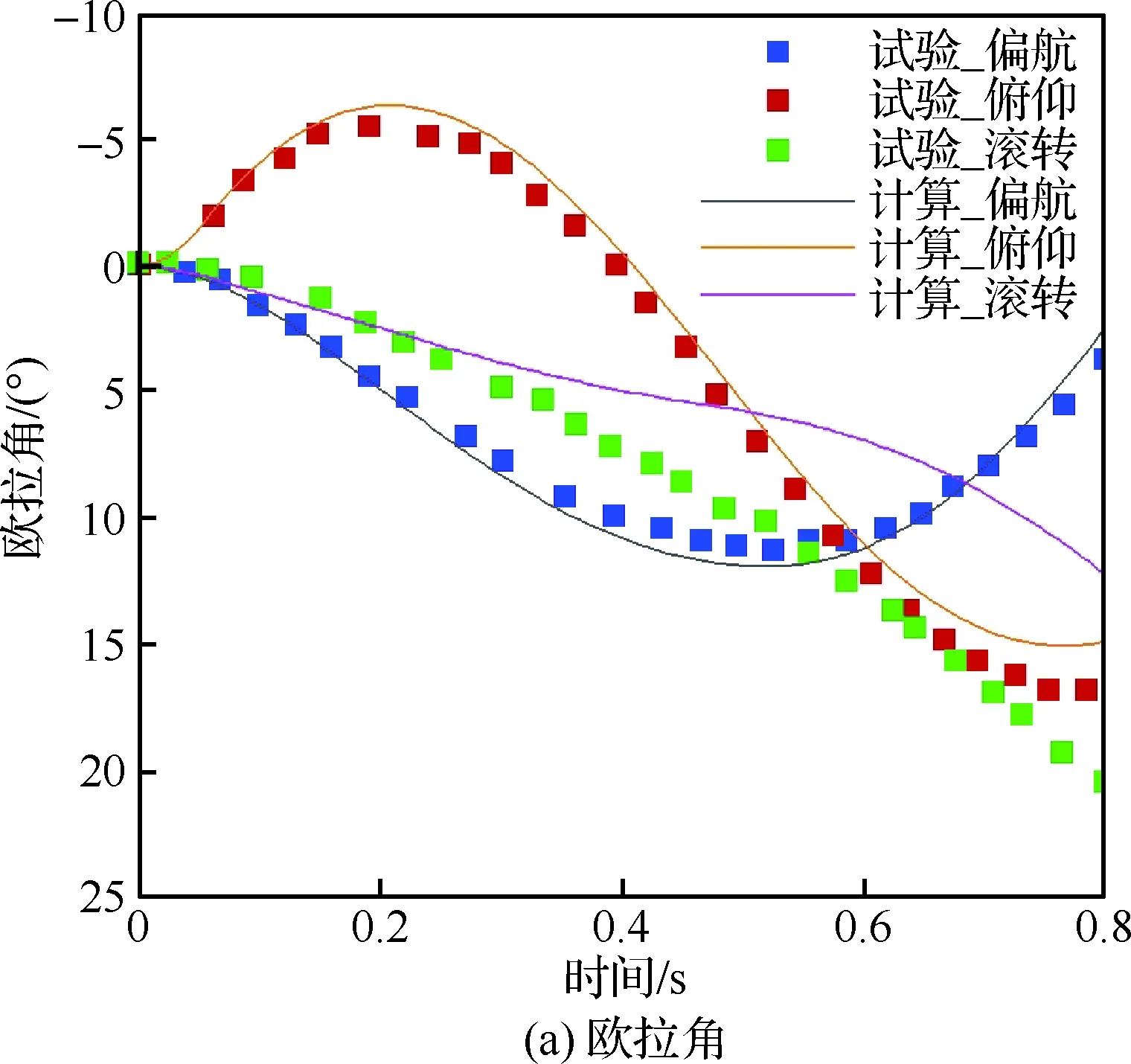
图15 外挂物运动参数的CFD结果与试验值的对比Fig.15 Comparison of CFD and test results of motion parameters of store

6 结 论

1) 发展了高效的KNN-RBF网格变形方法，解决了RBF方法计算效率低和支撑半径的选取问题。通过采用高效的数据结构，发展了网格分区节点一致性方法，实现了网格变形的并行化。

2) 在自主开发的非结构CFD程序中实现了编译型和解释型UDF功能，能够灵活设置动边界的运动规律，增强了程序求解含动边界非定常流动问题时的扩展能力。

3) 采用全局网格重构策略，解决了大变形情况下网格质量下降的问题。针对重构后流场的插值问题，提出了基于两级KD树的并行流场插值方法，具有高效、健壮和低耗散的特点，实现了并行条件下新旧网格流场的快速插值。

4) 通过模拟解析函数、翼型定常流动和外挂物投放等算例，验证了网格变形和流场插值方法的适用性。此外，两级KD树插值方法只需要网格点的坐标信息，对网格拓扑没有限制，不仅适用于非结构动网格，也可应用于重叠网格和滑移网格等网格类型的流场插值问题中。