动基座近舰面流场数值模拟
李旭,祝小平,周洲,*,郭佳豪
1. 西北工业大学 航空学院,西安 710072 2. 西北工业大学 无人机特种技术重点实验室,西安 710065
航空母舰是舰载机活动的重要场所,其甲板的流动将直接影响舰载机能否安全起降。因此,对航母甲板流场的研究就显得非常重要。通常,舰船气流场是以分离流为主要特征的流场,分离区的流动对旋翼和固定翼的正常作业均会产生较大影响[1]。对航母而言,气流经过舰首一般会产生上洗,遇到舰岛时,会在其后方形成大的分离区,而当气流到舰尾时,又会突然下沉然后再上升,形成公鸡尾流[2]。同时,实际航行中,航母还会出现一定程度的摇晃[3-4],复杂的流场使得舰载机的起降变得更加困难。因此,只有对航母流场有一个清楚的认识,才能为舰载机的安全起降提供指导。
目前,对孤立舰船流场的研究,可分为静止和运动两种状况。静止舰船流场的研究相对较多,主要有:Polsky等[5-7]对两栖攻击舰(LHA)和核动力航母(CVN)模型进行了一系列的计算,其研究了雷诺数无关性和马赫数无关性,表明网格质量对分离区流动的预测至关重要;郜冶等[8-10]采用雷诺平均Navier-Stokes(RANS)方程对不同风向下舰船的流场进行了研究,结果显示岛型建筑的形状和位置对下游气流场涡旋结构的形态影响较大。与此相比,舰船处于运动状态下气流场的研究还比较有限。王伟[11]采用Fluent研究了俄罗斯某大型舰船(RCSM)在横摇运动中的气流场特性,发现在船体角速度最大的位置,运动对甲板上流场的影响更加突出;安军[12]基于混合网格,采用动网格技术和VOF(Volume of Fluid)法对航母在俯仰和垂荡情况下的尾流进行了分析,表明飞机下滑轨迹上垂向速度波动的周期性相比水平方向更明显。此外,还有一些文献对舰船的耐波性和自由液面的精确模拟[13-14]进行了研究。
近几年,随着CFD技术的进步,舰载机和舰船耦合流场的研究逐渐兴起,主要有:郜冶和谢辉松[15]研究了舰载机滑跃起飞过程对舰面气流分布的影响,表明飞机起飞时对甲板上方流场有较大影响,但运动时飞机的飞行高度没有变化,且缺少对舰载机本身气动特性的分析;Crozon等[16]利用HMB2代码计算了旋翼和加拿大巡逻护卫舰(CPF)的相互干扰,对比了激励盘模型和真实桨叶的差别,表明利用定常计算的激励盘模型可以较好地预测流场的主要特征;苏大成等[17]采用动量源的方法对旋翼进行等效,对直升机着舰过程中的复杂干扰进行了分析,进一步验证了动量源对干扰流场模拟的有效性。
可以看出,旋翼和舰船的耦合流场研究相对较多,且重点在旋翼的等效[18-19]和舰面流场的重构[20]上,已经取得了一些成果。而固定翼飞机与航母耦合流场的研究相对较少,特别是缺少在航母运动情况下固定翼飞机着舰的数值模拟。已有的一些研究只是根据简化的尾流模型[21]对舰载机的着舰进行飞行力学仿真,但很难刻画出耦合流场的真实特性。
针对固定翼飞机着舰数值研究较少的现状,本文开展了在航母复杂风场下舰载机的着舰模拟。基于商业软件Fluent,以飞翼无人机为研究对象,进行了航母运动情况下无人机着舰流场的计算与分析。首先,通过与已有试验数据的对比,找到适合于舰船流场模拟和动边界计算的数值方法;然后,通过对网格局部加密、水面影响等因素进行分析,确立适合本文动基座近舰面流场计算的数值模拟方法;最后,分别在航母垂荡处于不同相位的情况下,对无人机的着舰过程进行分析,为舰载机的着舰仿真和控制提供参考。
1 计算方法与算例验证
1.1 SFS2舰船算例
为了验证本文建立的舰船流场数值模拟方法的可靠性,选用国内外常用的简单护卫舰SFS2(Simple Frigate Shape2)作为验证模型[22],如图1所示。其主要尺寸为:长l=138.684 m,宽b=13.716 m,高h=16.764 m。
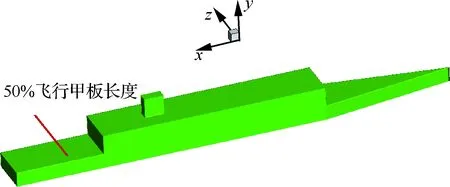
图1 SFS2模型Fig.1 SFS2 model
脱体涡模拟(Detached Eddy Simulation, DES)在对大尺度分离涡预测上优势明显,因此本文研究了其与RANS方程在舰船流场模拟上的差异。另外,考虑到不关心船本身的受力特性,同时也为了减少网格量,基于RANS方程,本文又对比了SFS2表面有/无附面层对计算结果的影响。其中,无附面层的网格为409万,有附面层的网格为533万,两种网格对比如图2所示。
湍流模型均采用剪切应力输运(SST)k-ω[23],计算条件为不可压、海平面标准大气压。在飞行甲板长度50%处(如图1线段所示)、高度与机库平齐处沿z轴取一条长度为船宽b的线段,取这条线段上3个方向的速度(非定常计算为时均结果),无量纲化后与试验结果的对比如图3所示,V∞表示自由来流速度,Vx,Vy,Vz分别对应图1坐标系中3个方向的分速度。
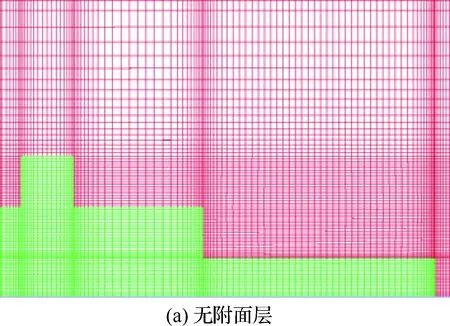
图2 不同网格比较Fig.2 Comparisons of different meshes
由图3可知,整体来看4种计算状态得到的结果趋势基本一致,但DES计算的3个方向的速度能与试验更好的吻合,差别主要体现在x方向的速度上。同时,还可以看出利用RANS计算时,有附面层和无附面层的网格计算结果差别不是很大,定常计算与非定常时均的结果也类似。
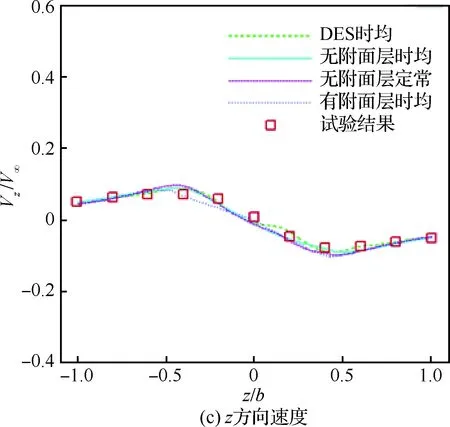
图3 SFS2数值计算与试验的对比Fig.3 Comparison of SFS2 using CFD and test
虽然DES计算的精度更好些,但其计算花费最大,考虑到之后的计算需要耦合无人机着舰,采用RANS方法对航母流场进行模拟是比较可行的,且能够满足一定的精度。
1.2 计算模型
本文使用的航母和无人机模型如图4所示。航母甲板为斜直两段式,坐标原点位于静止航母船首甲板最左端的顶点,长260 m,宽60 m,吃水10 m,水线以上高度为44.782 m,甲板距水线15 m 左右。3个轴的方向如图4(a)所示,且坐标系不随航母运动而发生变化。无人机对地速度大小为60 m/s,其下滑轨迹的投影通过航母斜甲板中心线,与x轴夹角为9°,如图4(b)所示。无人机下滑角为4°,航迹角为0°,求得无人机对地3个方向的速度分别为:Vx=-59.116 9 m/s,Vy=-9.363 2 m/s,Vz=-4.185 4 m/s。
取风的速度为15 m/s,当风向为0°时,无人机相对于空气的速度为:Vx=74.116 9 m/s,Vy=9.363 2 m/s,Vz=4.185 4 m/s,合速度V=74.823 1 m/s,迎角α=3.208 2°,侧滑角β=1.797 1°,为右侧滑。
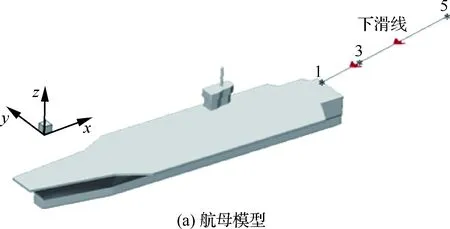

图4 计算模型Fig.4 Calculation model
考虑计算花费,选取无人机着舰阶段最后2 s进行数值模拟。无人机起始重心坐标为(371.832 6,30.595 3,13.188 0),匀速降落2 s后,重心坐标为(253.598 8,11.868 8,4.817 0),此时无人机完全处于甲板上方,分析该阶段无人机在穿越航母尾迹过程中气动特性的变化。
1.3 嵌套网格验证
由于航母和无人机尺寸差别巨大,因此,在建立背景网格时,需要考虑二者的尺寸和运动特点,合理划分网格,从而减少网格量。在航母运动区域和无人机着舰区域进行局部加密,如图5所示。
为了验证局部加密网格的可靠性,对无人机不采用嵌套定常计算的结果和嵌套计算的结果进行比较。采用不可压RANS方程,非定常计算时间步长Δt=0.005 s,内迭代次数为10,无人机无附面层。
计算结果如图6所示,Ca表示气动力系数,包括升力系数CL和阻力系数CD;Cm表示气动力矩系数,包括俯仰力矩系数Cmy,滚装力矩系数Cmx和偏航力矩系数Cmz。通过计算可以发现,采用局部加密网格计算得到的气动力和力距与定常计算的结果基本一致,表明可以利用局部加密的方法来减少网格量,所建立的嵌套网格是可行的。同时,还可以看出,在0°风向下,有/无附面层对无人机气动特性没有大的影响。因此,可采用无附面层的网格进行无人机着舰计算。

图5 局部加密嵌套网格Fig.5 Overset mesh of local refine
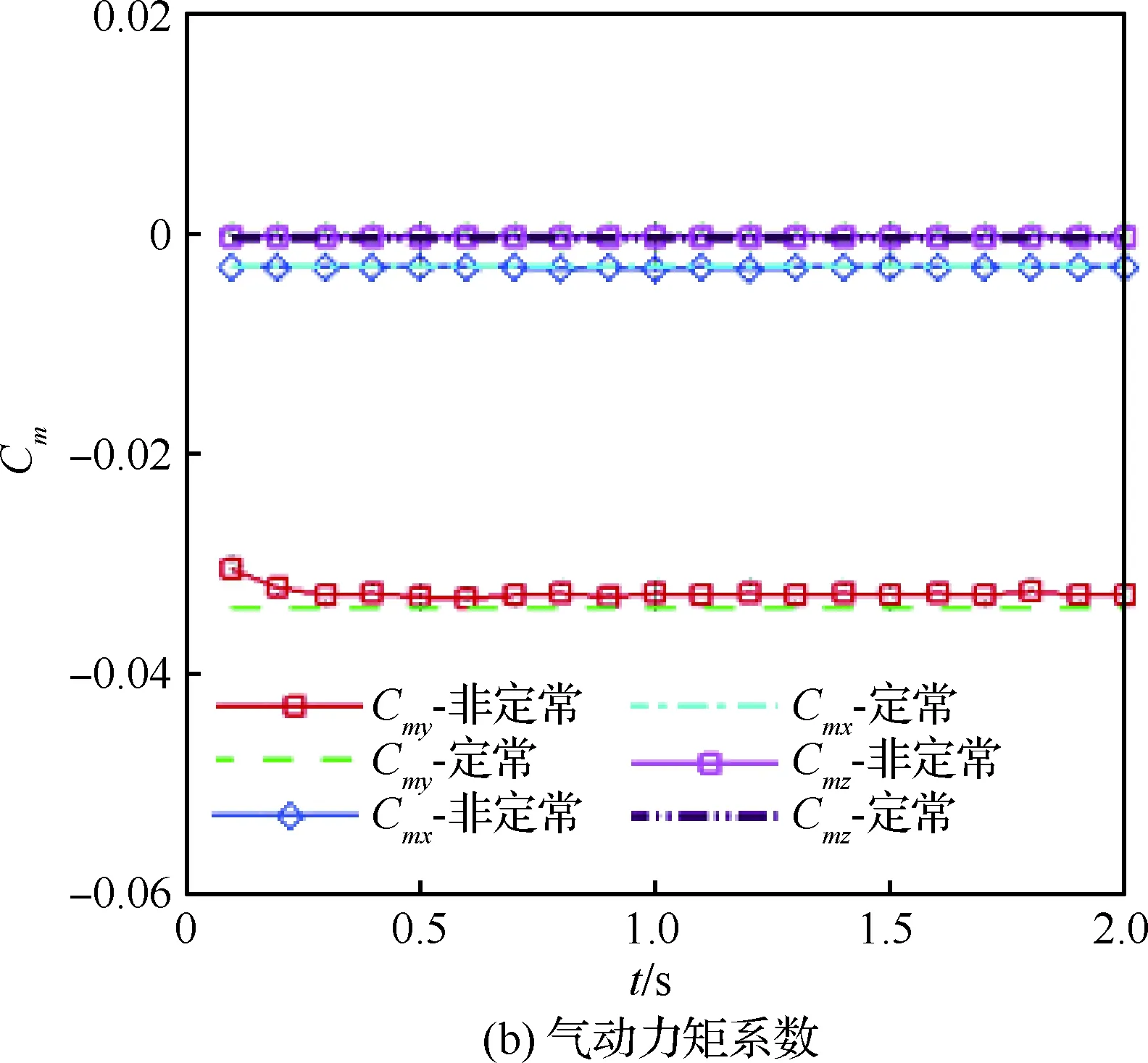
图6 局部加密计算验证Fig.6 Verification of local refine computation
1.4 水面影响分析
为了比较水面对航母流场的影响,将航母分别在单相流和两相流中的流场进行了对比。4种计算状态分别为
状态1单相流,网格没有嵌套,介质为空气,来流沿x正方向,速度为15 m/s,航母悬空,完全处于空气之中,进行定常计算。
状态2单相流,采用嵌套网格,介质为空气,来流沿x正方向,速度为15 m/s,航母悬空,完全处于空气之中,进行定常计算。
状态3两相流,网格没有嵌套,介质为空气和水,速度均沿x正方向,大小为15 m/s,航母处于气液两相流中,采用VOF方法对自由液面进行捕捉,取时均结果。
状态4航母水线以下部分被切除,海平面设为物面,取0°风向下定常计算的结果。
采用压力速度耦合算法,速度入口和压力出口边界,SSTk-ω湍流模型,非定常计算时间步长Δt=0.005 s,内迭代次数为10次。
两相流计算波形如图7所示。由图可知,航母的两侧存在明显的Kelvin波,表明计算较好地捕捉到了自由液面。截取x=210 m截面,比较甲板上的速度。
从图8速度云图可以看出,图8(c)和图8(d)中,航母在两侧受水面和物面的影响,速度分布与图8(a)和图8(b)存在差异,但4种情况计算的甲板上的流场速度分布基本一致,表明甲板上的流场受下方流动影响较小。
对比无人机下滑轨迹(图4(a))上的速度分布,如图9所示。由图可以看出,虽然下滑轨迹3个方向速度在数值上存在一些差异,但其变化趋势基本一致。这表明,不管是有水或没水,或者航母处于悬空状态,甲板下方的流动对甲板上方及着舰区域的流场影响不大。同时,也表明状态2的嵌套网格适用于航母流场的计算。
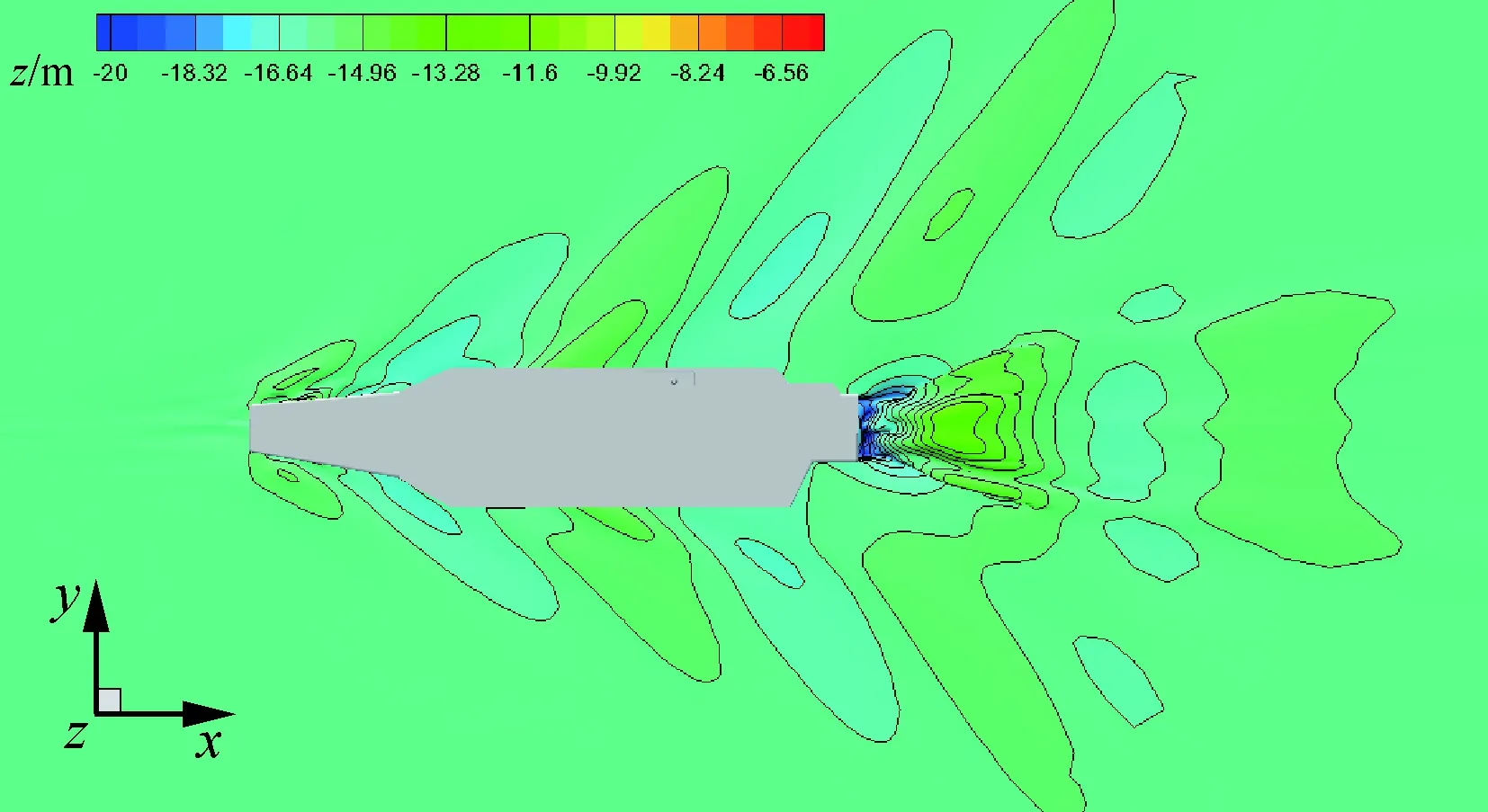
图7 自由液面波Fig.7 Free water surface wave
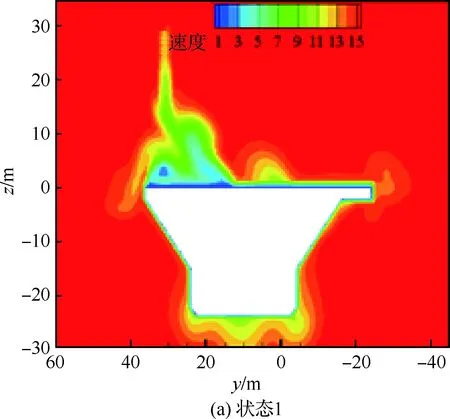
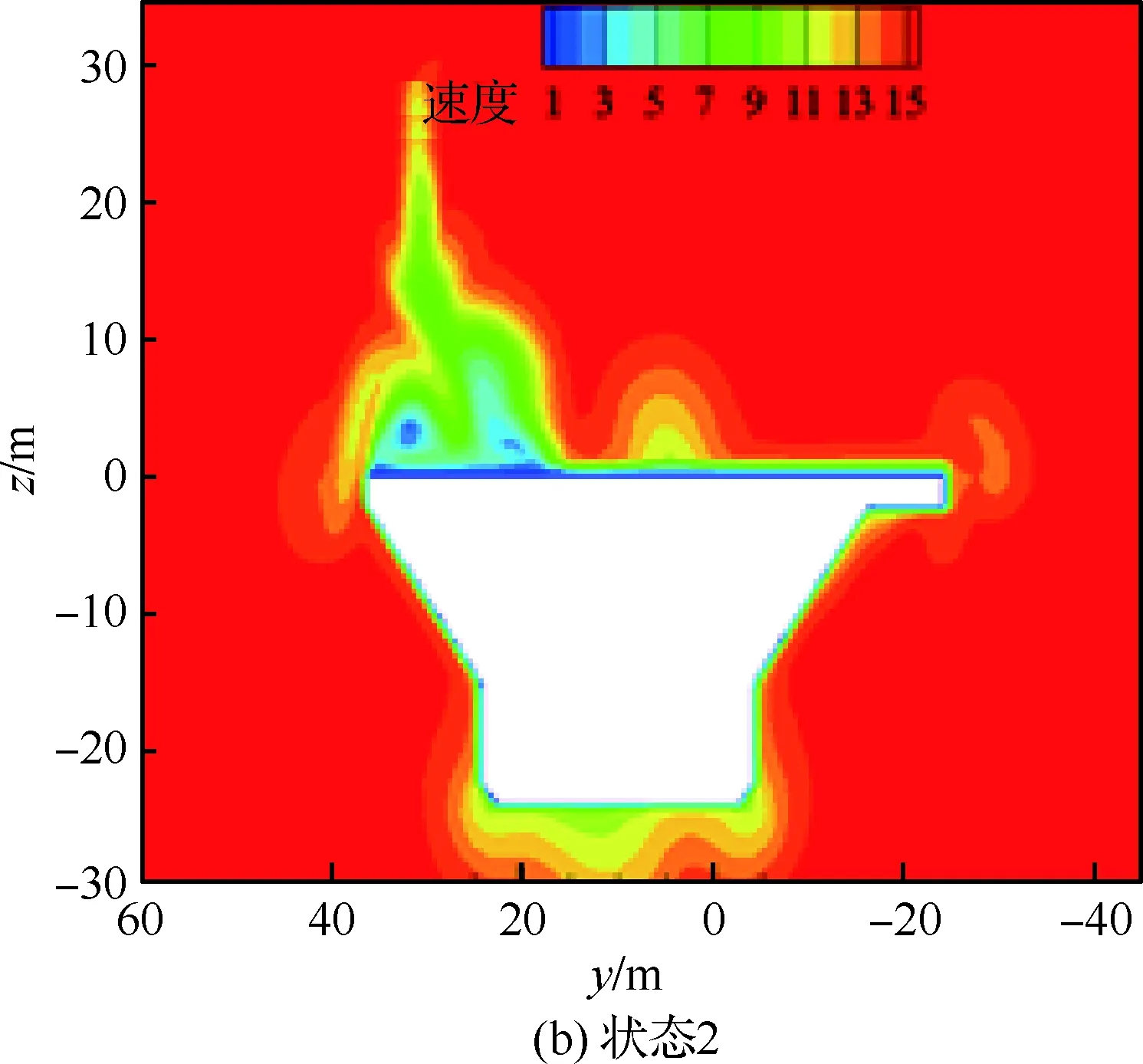
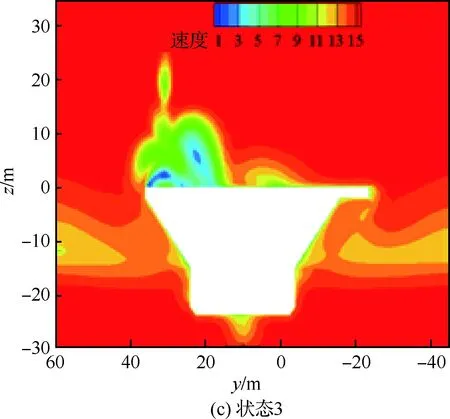
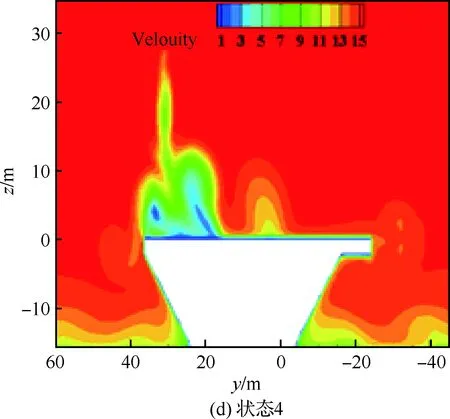
图8 参考截面速度比较Fig.8 Comparison of velocities at reference cross-section
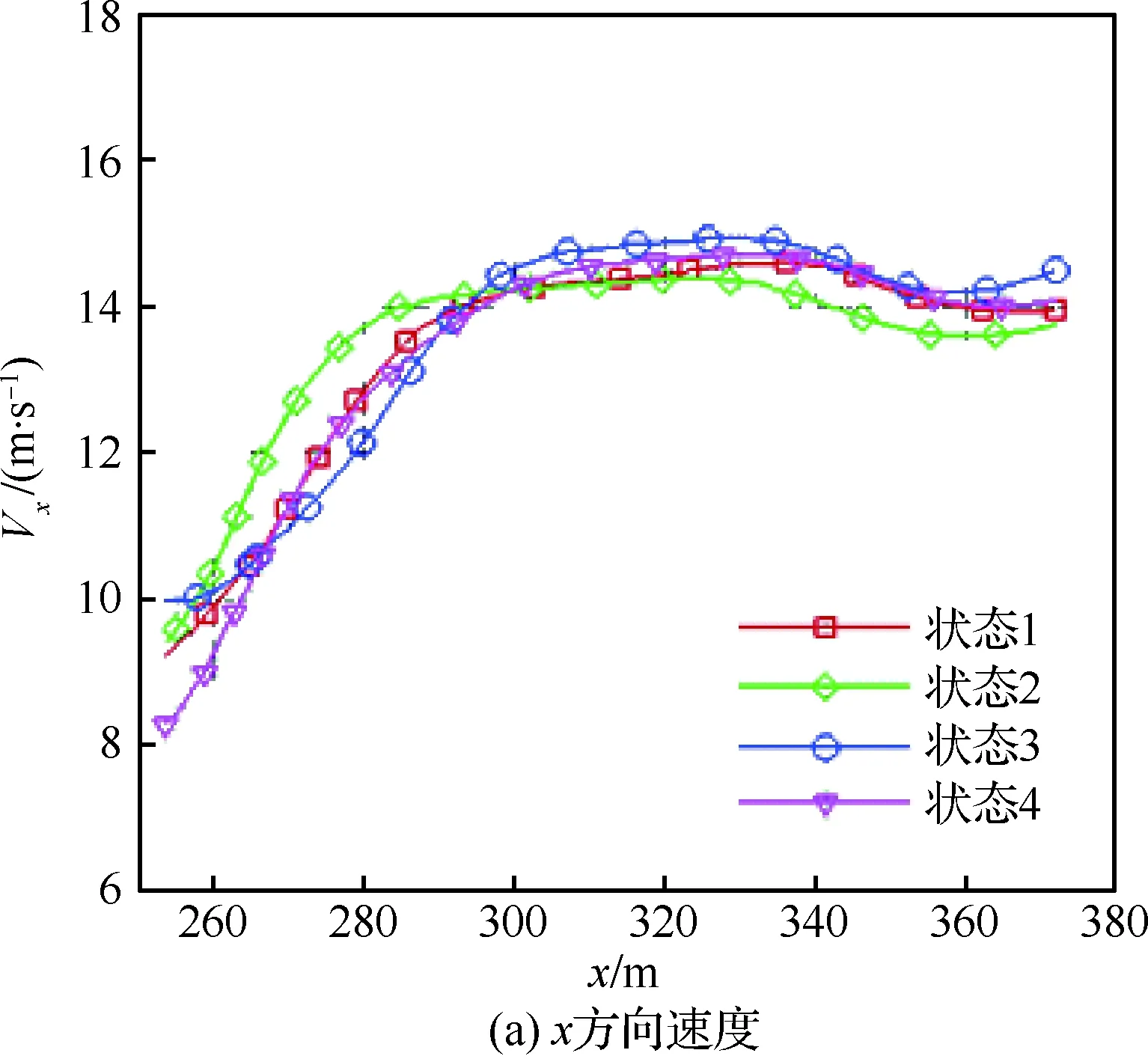
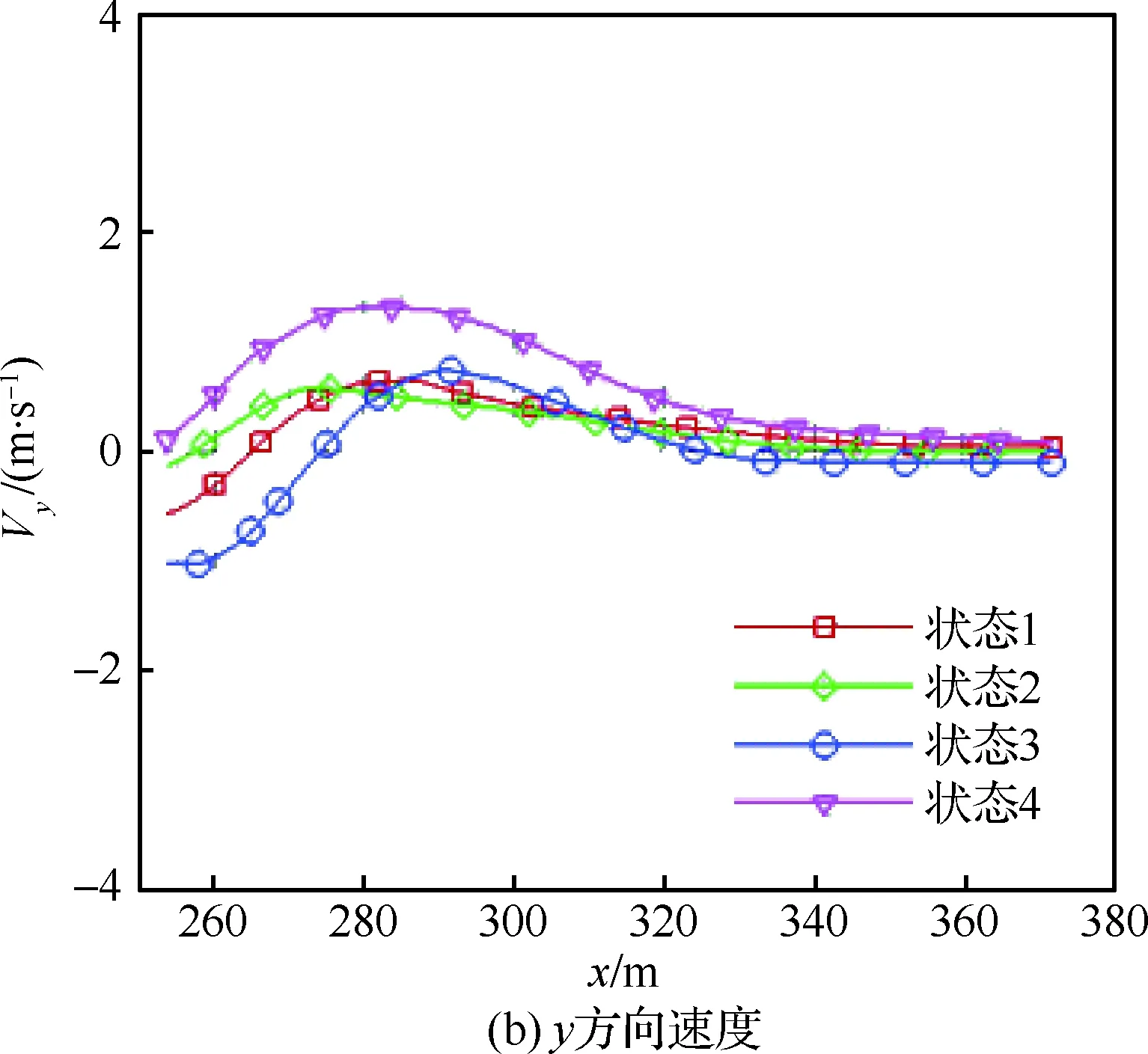
图9 下滑轨迹速度比较Fig.9 Comparison of velocities of landing track
再取两相流计算y=10 m截面,航母尾部流场如图10所示,表明航母尾部的自由液面是不平整的,这使得此处的流动会发生一定变化。但是由于航母的甲板以及无人机着舰区域距水面较远,因此水面对其上方的流场没有明显的影响。
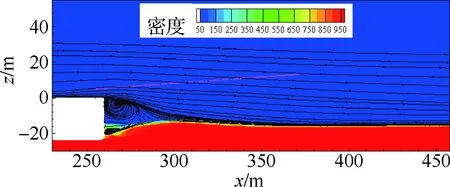
图10 两相流航母尾迹Fig.10 Ship airwake in two-phase flow
由于两相流计算非常耗费时间,为简化计算,之后对航母和无人机着舰的计算,均忽略了水的影响,采用在空气中运动的方式。
2 孤立航母流场
航母航行时的运动如图11所示,OsXsYsZs为航母体轴坐标系[2]。美国海军规定[4]无人机着舰时,航母的横摇不能超过7°、纵摇不能超过2°、舰尾下沉或上升不能大于1.5 m,从而保证舰载机能安全着舰。由于垂荡对航母流场影响比较明显,因此本文只研究了垂荡,航母垂荡的周期取T=4 s,运动方式为
H(m)=1.5sin(0.5πt)
(1)
航母的垂荡幅值为1.5 m,当无人机运动2 s时,航母运动刚好半个周期。当垂荡处于0°相位时,航母位移为0 m,其上升速度最大;当垂荡处于180°相位时,航母位移为0 m,其下降速度最大。
首先,利用单独航母进行网格无关性验证。生成3套嵌套网格,网格量分别为305万,450万和600万,对静止航母进行非定常计算,取下滑轨迹3个方向时均速度进行对比。如图12所示,可以看出,3套嵌套网格计算得到的下滑轨迹上的时均速度基本一致。从减小计算花费的角度出发,以后可采用第1套网格进行计算。
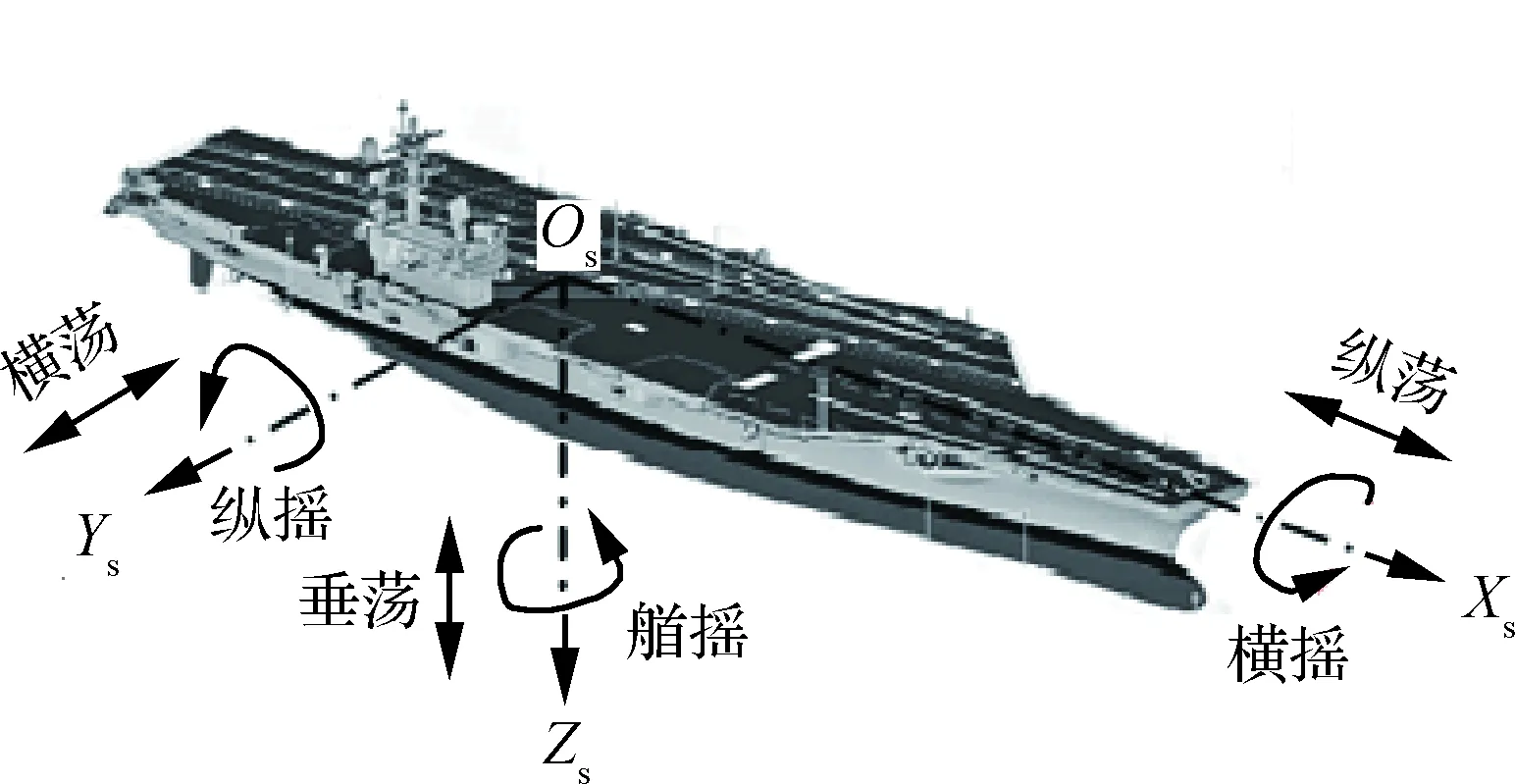
图11 航母运动示意图[2]Fig.11 Schematic of ship motion[2]
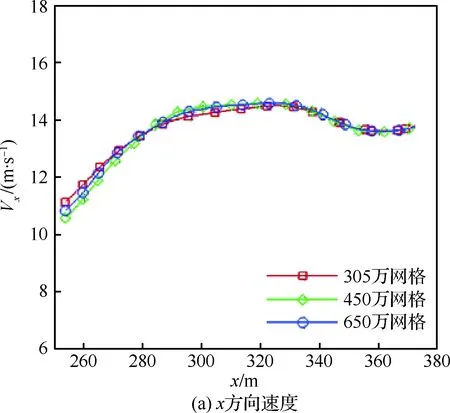
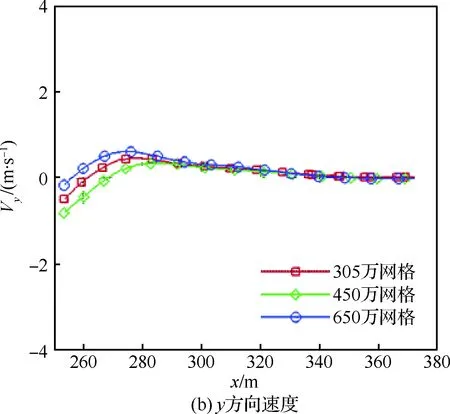
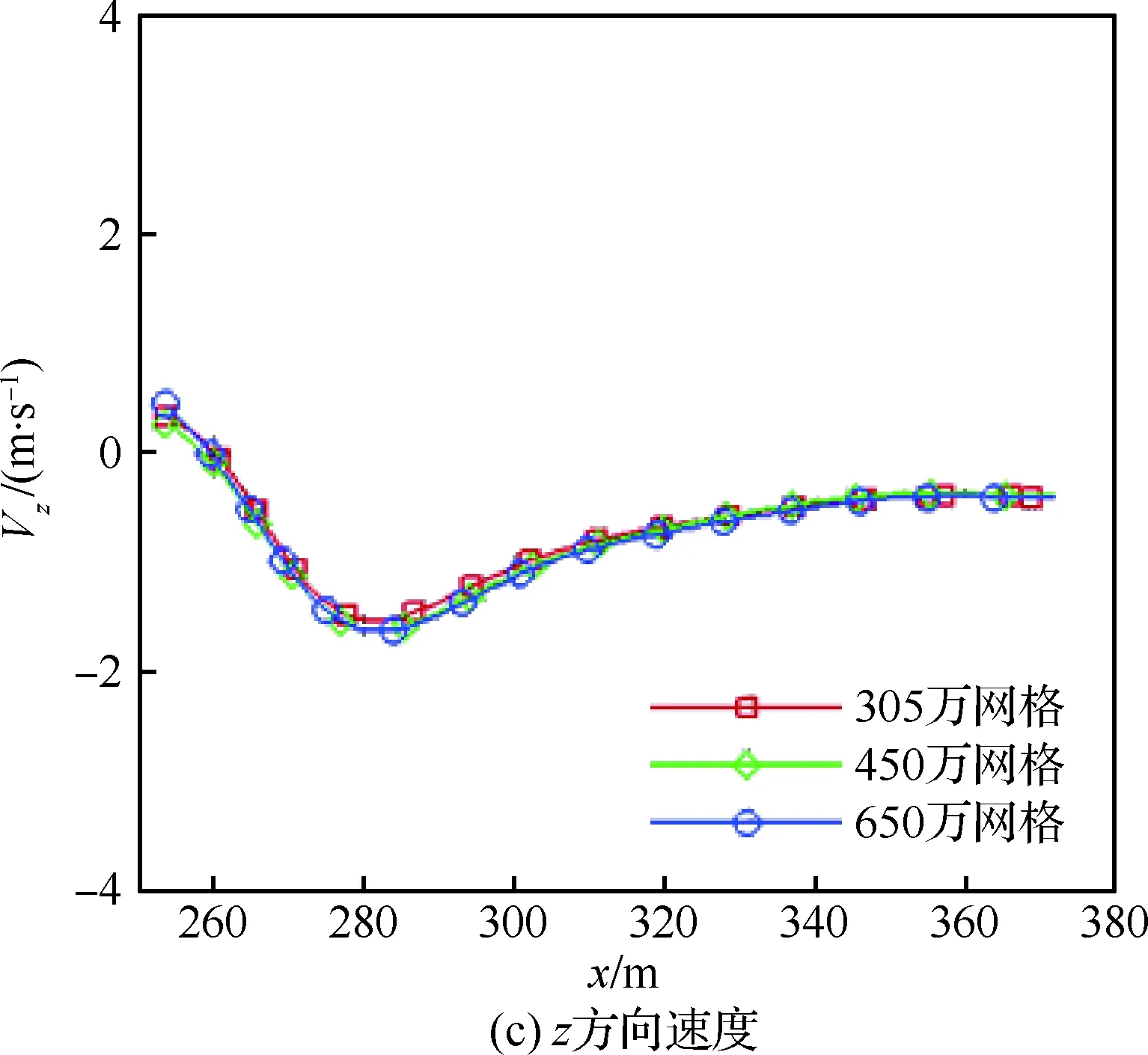
图12 不同网格时均速度比较Fig.12 Comparison of time-averaged velocities at different mesh quantities
因此,最终确定航母、无人机、背景网格的网格参数如表1所示。利用确定的网格,对单独航母进行垂荡计算,运动过程中航母阻力D曲线如图13所示。由图可知,航母的垂荡运动使得其阻力也呈现出周期性的变化,在t>32 s后,阻力振荡幅值基本稳定,表明运动加载是正确的。
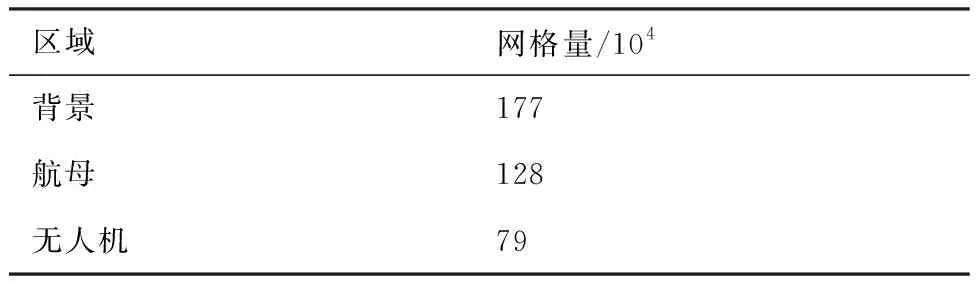
表1 网格参数Table 1 Mesh parameters
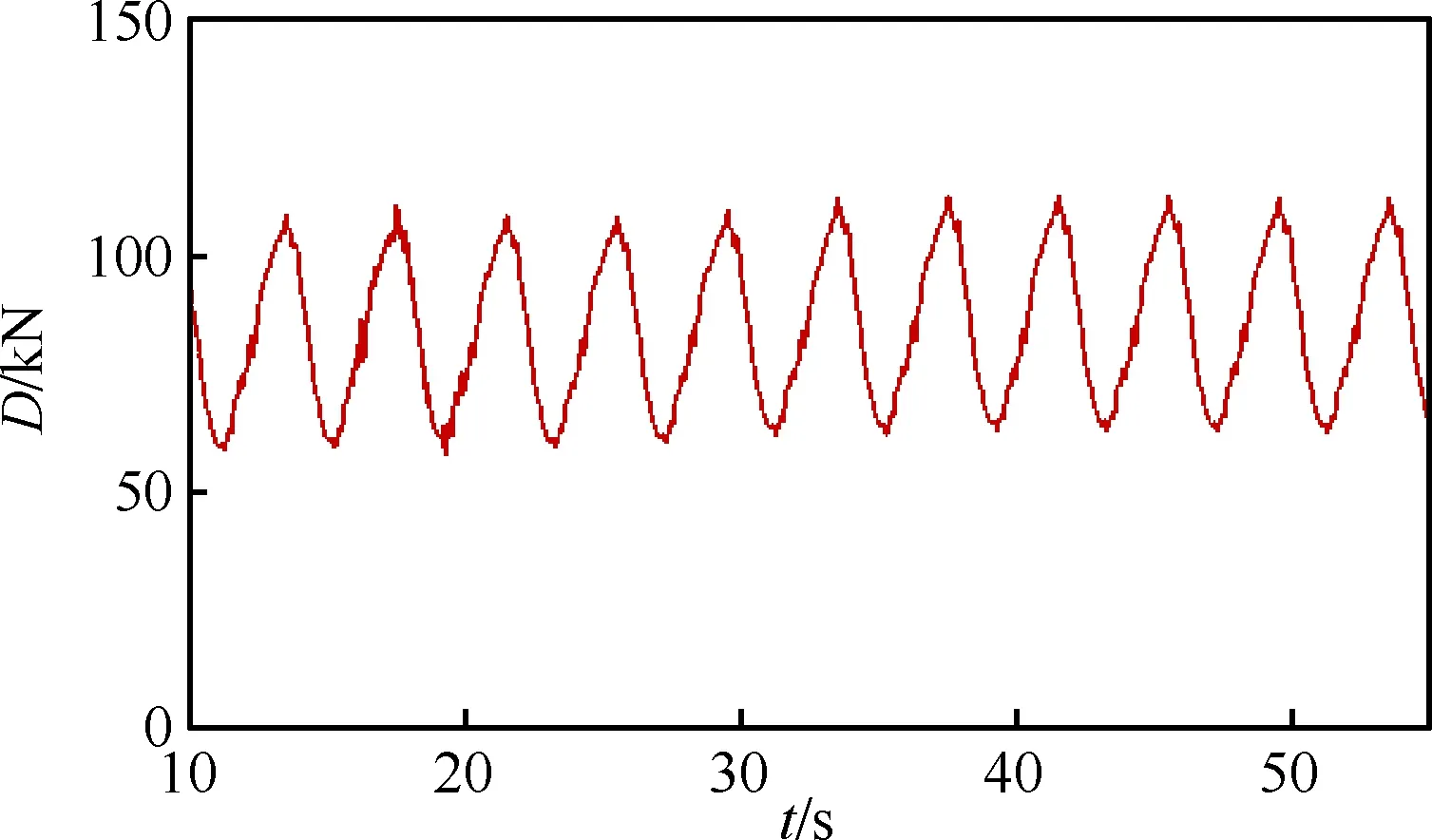
图13 航母垂荡阻力曲线Fig.13 Drag history of aircraft carrier in heave motion
2.1 三维流场
利用Q准则[24]对尾流的涡结构进行判断。取Q=0.003等值面,在t=36 s时刻,比较静止航母和运动航母的流场涡结构,如图14 所示。由图14(a)可知,对于静止航母,在舰岛后方和航母尾部中间区域存在周期性脱落涡,且涡结构尺度较大;当航母做正弦垂荡运动时,由图14(b)可知,航母两侧和舰首均存在向后脱落的涡结构,在航母尾迹区域涡的分布更加复杂,且以小尺度涡为主。由此可知,无人机在航母处于不同运动状态下着舰,将遭遇不同结构的流场。
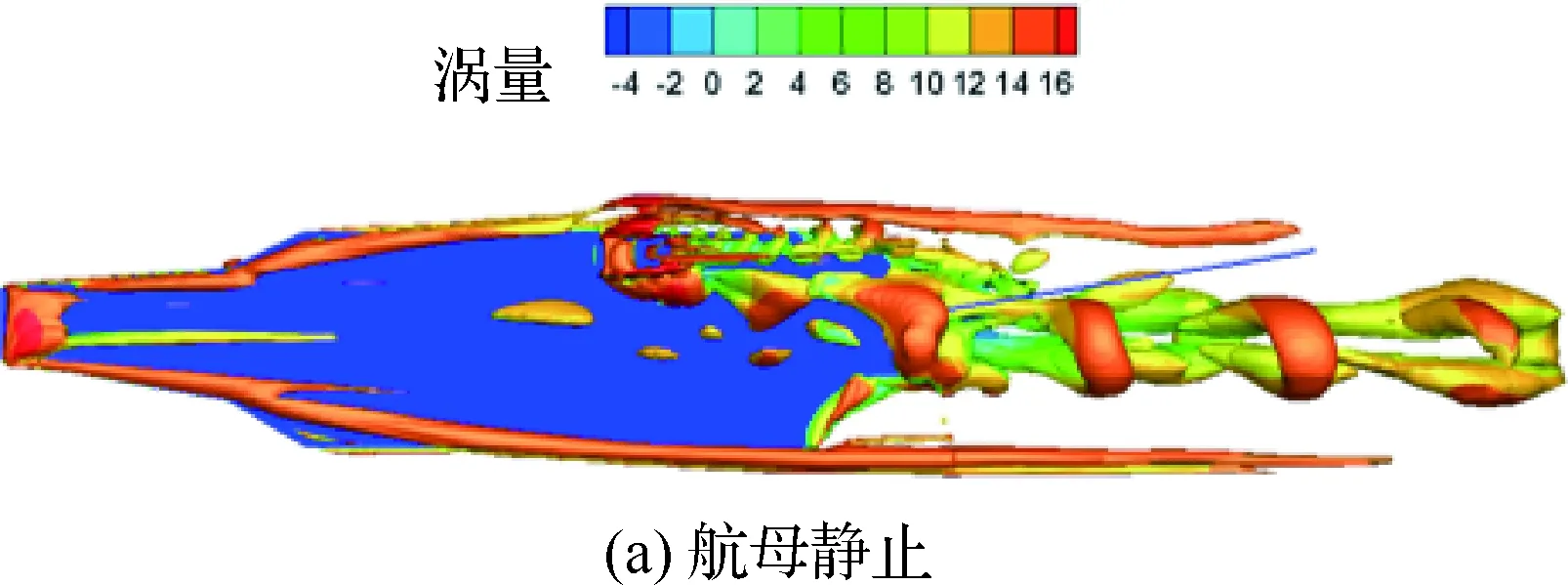
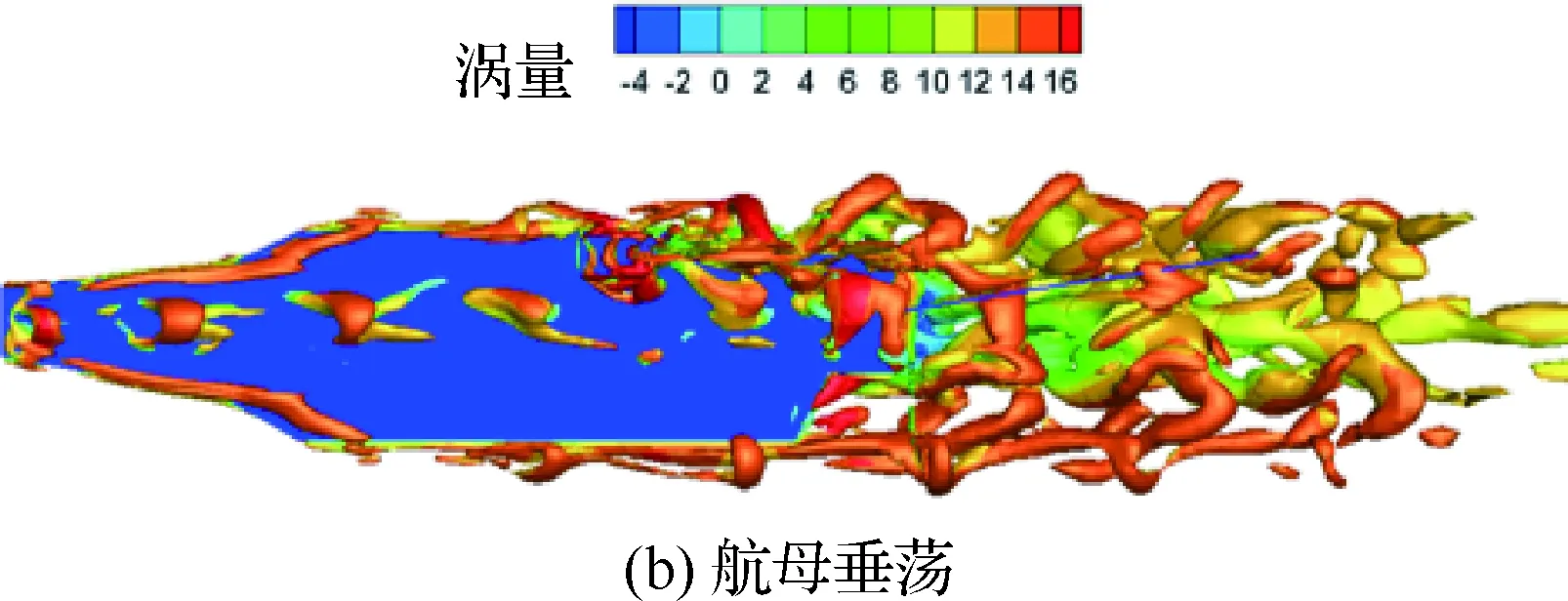
图14 等值涡结构比较Fig.14 Comparison of iso-surfaces of vorticity
2.2 尾迹速度
航母尾迹的流动会直接影响无人机着舰。为了对尾迹速度有一个更清楚的认识,有必要对航母静止和垂荡时无人机下滑轨迹上的速度进行研究。
首先,根据图4(a),取无人机下滑轨迹上的监视点1、监视点3和监视点5,对这3点速度随时间的变化进行分析(如图15所示),3点对应的x坐标分别为x=253.6,289.1,371.8 m。
由图15可知,t=10 s以后,静止航母监视点的速度呈现出周期性的变化,周期大约是4~5 s,且随着远离航母速度波动的幅值逐渐减弱,在监视点5的位置速度基本没有变化。由于监视点1在甲板上方,甲板上存在分离涡,如图14(a)所示,因而影响最明显。相比静止航母,运动航母的流场变得更加复杂。从图15(f)可以看出,由于垂荡的作用,3个监视点的Vz振荡幅值均有所增强,这将对无人机的正常着舰带来更大影响。
取不同时刻无人机下滑轨迹上的速度分布进行对比,如图16所示。由图16(a)~图16(c)可以看出,静止航母速度的波动集中于x<300 m,更加靠近航母尾部。而在航母垂荡时,整个下滑轨迹上的速度一直处于波动的状态,特别是图16(f)中的Vz,在t=34.0 s时,x=260~280 m,Vz的变化幅值高达4 m/s。相比静止航母,运动航母的尾迹流场变得更加复杂,与图14的结论是一致的。
由于垂荡情况下,航母流场波动剧烈,很难根据某个时刻下滑轨迹上的速度分布来分析无人机着舰过程中气动力的变化。因此,根据无人机的着舰过程,时间间隔取0.1 s,将单独航母静止和运动情况下无人机下滑轨迹不同时刻的速度进行对比,如图17所示。其中,着舰1指0°相位着舰,32.0~34.0 s内无人机下滑轨迹不同时刻的速度分布;着舰2指180°相位着舰,34.0 s~36.0 s内无人机下滑轨迹不同时刻的速度分布。由图可知,不同相位下着舰,无人机下滑轨迹的速度分布是不同的。
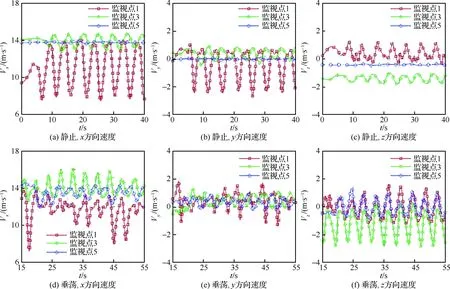
图15 监视点速度比较Fig.15 Comparisons of velocities at monitor points
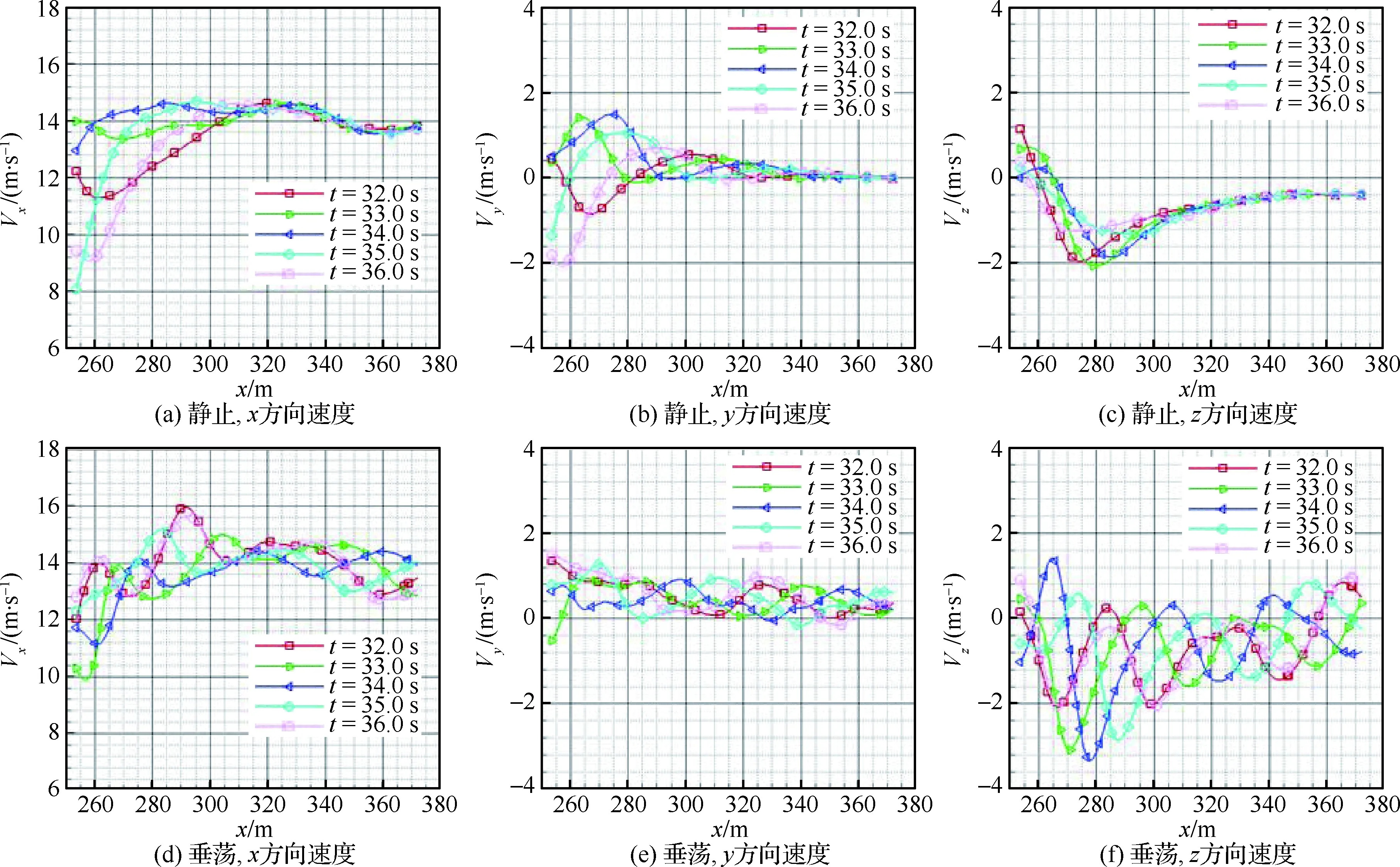
图16 下滑轨迹速度比较Fig.16 Comparisons of velocities of landing track
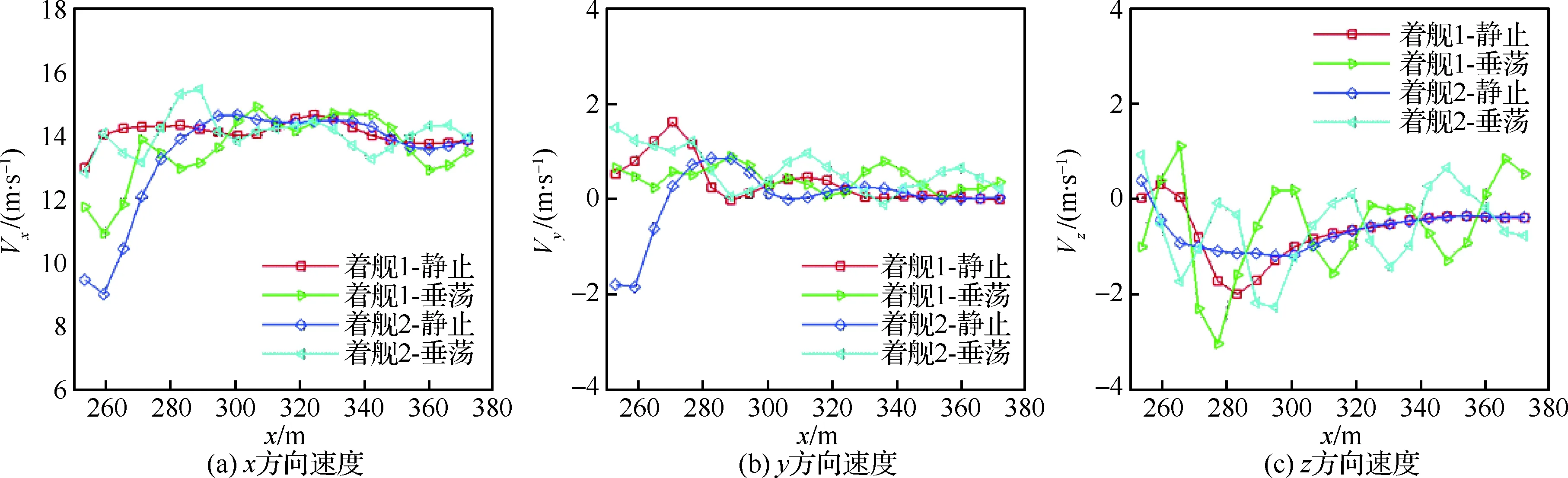
图17 着舰过程下滑轨迹速度Fig.17 Velocities of landing track during carrier landing
3 舰载机/航母耦合流场分析
对单独运动航母的流场进行研究后,就需要进一步耦合无人机,进行动基座无人机着舰的研究。从第2节计算可以看出,不同相位情况下,下滑轨迹的速度分布是不同的,因此,当无人机在航母处于不同相位的情况下着舰时,其遭遇的流场有差异,需要加以分析。本节对0°和180°两种相位下无人机的着舰过程进行模拟,比较两种情况下无人机气动特性变化的差异。
计算采用的网格结构如图18所示。在计算过程中,航母和无人机区域的网格将按照指定方式进行运动,计算过程中嵌套的边界不断更新,进行流场信息的传递。
取航母垂荡情况下t=33.0 s时,有/无无人机存在两种状态,无人机下滑面上的Vz对比如图19 所示。在t=33.0 s时,无人机降落刚好1 s。 从图19(a)可知,x=312.7 m的四周都是下洗区,无人机运动到此处升力必然要减小。在x>312.7 m时,无人机运动经过的区域其后方下洗明显,与单独航母的速度差异明显;在x<312.7 m 时,无人机还未运动到的地方,图19(a)和图19(b)的Vz分布基本一致,表明无人机对其前方较远的流场影响不是很大,其余各个时刻也有类似的结论。因此,可以用单独航母流场来分析无人机着舰过程中气动特性的变化。
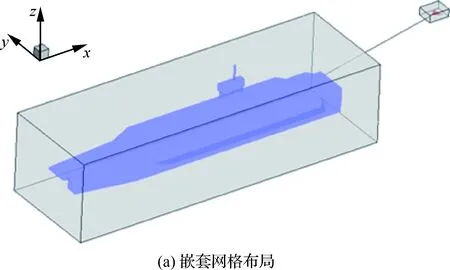
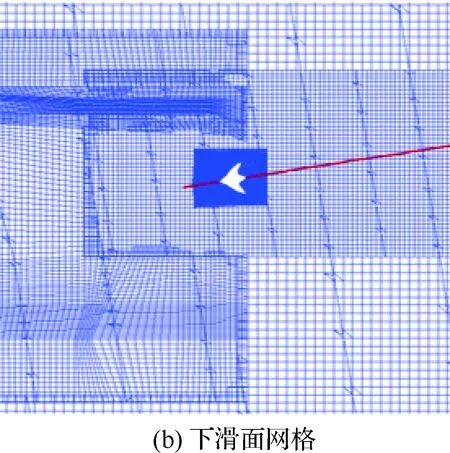
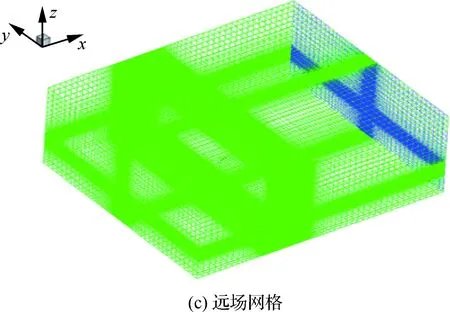
图18 网格布局Fig.18 Mesh layout
3.1 0°相位着舰
由于无人机的着舰时间是航母运动周期的一半。因此,此时开始着舰,航母会先向上运动再向下运动,回到平衡位置时,无人机刚好完成着舰,和航母的相对高度与航母静止时着舰保持一致。计算时间为32.0~34.0 s,分别在航母静止和垂荡的情况下,对无人机运动过程中的气动特性进行比较,如图20所示。
由图20看出,对于本文的垂荡运动而言,航母运动引发的小尺度的涡使得无人机着舰气动特性变化更加剧烈,这主要和降落时当地流场的速度有关。结合图17(c)可知,升力的变化和相应状态Vz的变化是一致的,上洗最大的地方,升力最大;下洗最明显的位置,升力最小。由于开始着舰时航母处于0°相位,无人机着舰运动1 s后,航母开始向下运动,这会带动甲板上方的气流也向下运动,因此,下洗会比较明显,从而导致在最后时刻,无人机的升力相比静基座着舰的情况出现下降。
3.2 180°相位着舰
此时无人机开始着舰,航母先向下运动,再向上运动,回到平衡位置时,无人机刚好完成着舰,无人机和航母的相对高度也和航母静止时着舰保持一致。
计算时间为34.0~36.0 s,无人机降落过程中的气动特性对比如图21所示。与图20(a)类似,对于静止航母流场,无人机气动力的变化比较缓和,短时间内没有出现大的波动,随着靠近航母,升力先下降,然后再上升。而在动基座的情况下,无人机的升力曲线一直表现出波动,且0°相位和180°相位无人机着舰升力的变化曲线正好相反。对于180°相位着舰而言,当无人机降落到航母甲板上方时,航母此时向上的速度达到最大。由于航母向上运动,同样会带动周围的气流也向上运动,具有上洗的效果。因此,在最后时刻无人机的升力会有所增大。
图19 下滑面Vz比较Fig.19 Comparison of Vz at landing surface
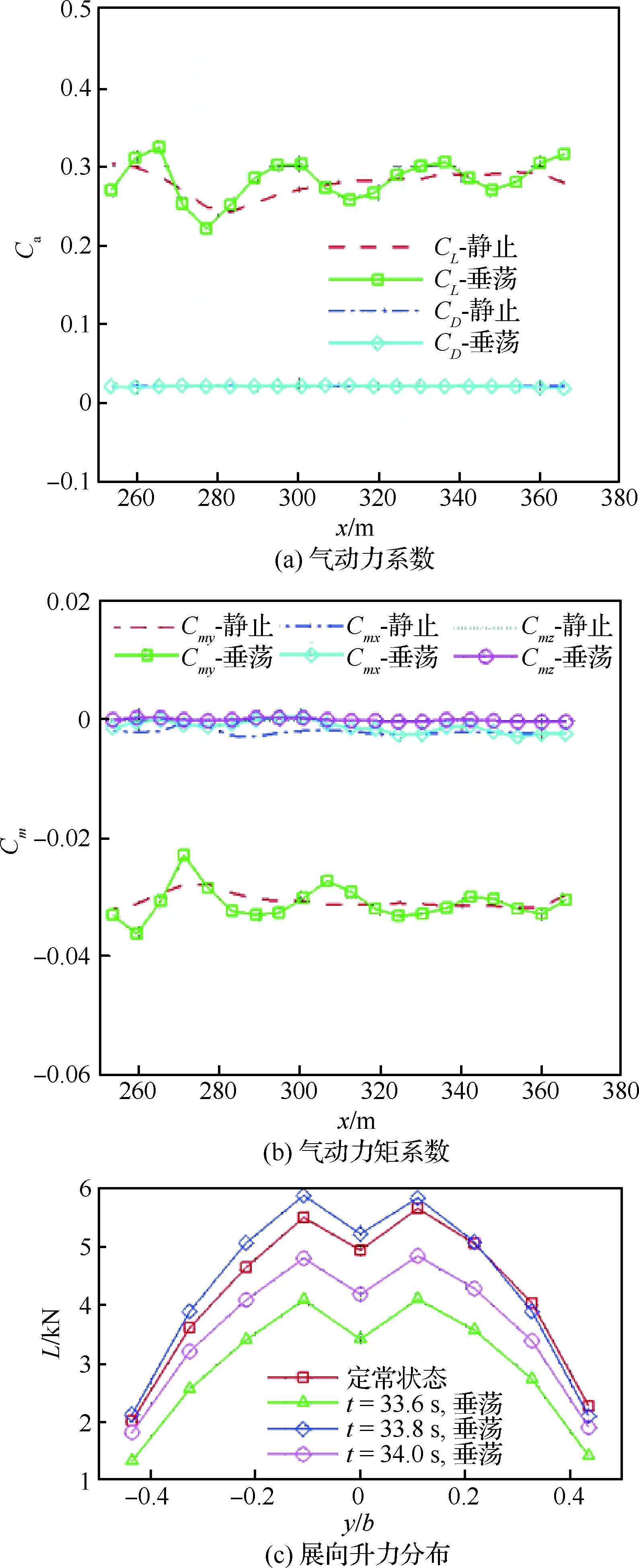
图20 0°相位着舰气动特性Fig.20 Landing aerodynamic characteristics at 0° phase
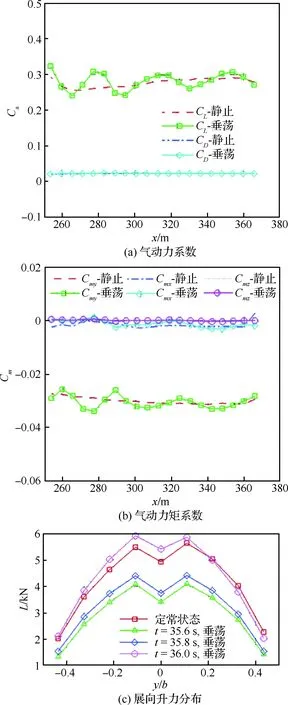
图21 180°相位着舰气动特性Fig.21 Landing aerodynamic characteristics at 180° phase
在航母垂荡情况下,基于Q等值面,取t=36.0 s 时无人机着舰的流场,如图22所示。由图可知,无人机经过的区域其后方两侧形成两条尾迹,而其余未受干扰的区域的涡结构保持与图14(b)单独航母时类似,表明固定翼无人机对舰船流场的影响区域有限。
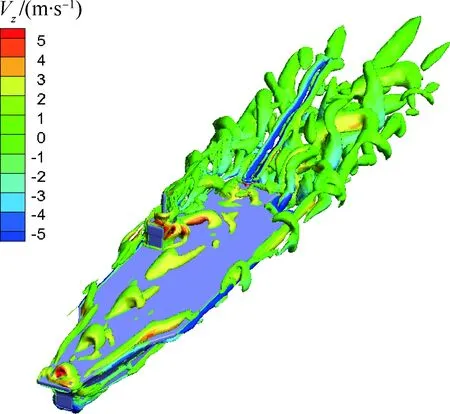
图22 耦合流场的Vz(t=36.0 s)Fig.22 Vz at coupled flow field (t=36.0 s)
4 结 论
本文对航母垂荡情况下无人机的着舰进行了模拟。首先,对舰船流场的计算方法进行了研究,对嵌套网格的可靠性进行了验证,接着对比了水面对舰船空气流场的影响,然后研究了静止航母和运动航母流场的差别,最后对航母垂荡处于不同相位时无人机着舰过程中的气动特性进行了分析。
1) 航母甲板一般距海平面较远,水面对甲板上的流场影响有限,当不考虑船和水的相互作用时,可忽略水的影响。另外,对于像舰载机着舰的多体运动问题,采用局部加密的嵌套网格有助于减少网格量。
2) 航母尾迹是一种时空上不断变化的流场,非定常特性明显。对于静止航母而言,尾迹3个方向速度均存在周期性明显的波动,且波动的幅值随着远离航母逐渐减小;而当航母垂荡时,尾迹水平方向的速度周期性减弱,但垂向速度的波动幅值显著增强,流动变得更加紊乱。
3) 无人机在着舰的过程中升力和俯仰力矩受尾迹的影响较大。升力的变化趋势与垂向速度的变化保持一致。对于静止航母,无人机在靠近其尾部的过程中升力会先减小然后再增大;而当航母处于垂荡状态时,无人机的升力和俯仰力矩会出现明显的波动,使得着舰更加困难。
4) 在耦合流场中,对于无人机运动经过的区域,其周围流场下洗明显增强,与孤立航母时的流场存在较大差异;而在远离无人机运动区域的地方,耦合流场的流动结构与孤立航母时的情况类似。

