结冰飞机着陆阶段飞行安全包线确定及操纵应对策略

周驰，李颖晖，郑无计，武朋玮，董泽洪

空军工程大学 航空工程学院，西安 710038

近年来由结冰所导致的飞行事故持续发生，结冰不仅会破坏飞机的动力学特性，同时也会对驾驶员的操纵造成严重影响。在未察觉结冰的情况下，飞行员的操纵极易使飞行状态超出飞行安全包线，最终引发飞行事故[1]。美国国家航空航天局(NASA)及联邦航空管理局(FAA)统计的1976—1994年间所发生的飞行事故，有16起与飞机结冰有关，并导致了139人死亡[2]。美国Safety Advisor[3]对1990—2000年间因气象原因造成的飞行事故进行了统计，其中结冰事故就占了12%。飞机遭受结冰影响，不仅升力减小，阻力增大，同时失速迎角也会相应减小，此时飞控系统可能会给机组提供一个错误的操纵指导，从而给飞行安全造成重大隐患，因此飞行包线确定对于提升飞行安全具有重要意义。传统的安全包线通常是在飞机的欧拉角、负载、飞行速度等飞行参量上加以限制，并认为只要不超出这些限制，飞机就能安全飞行[4]。但在环境因素(结冰、强风)等影响下，传统的安全包线就不再适用。1994年，美国鹰航公司的一架ATR72-212飞机坠毁于印第安纳Roselawn地区，当时飞机的飞行迎角仅为5°，这远低于飞控系统提供的迎角限制值18.1°，可是在机翼重度结冰的影响下，飞机仍然因失速而导致事故发生[5]。

为了保障飞行安全，必须建立能够考虑多种外在因素影响的飞行安全包线。近年来，国内外对于安全包线的确定方法进行了较为广泛的研究，其中ROA(Region Of Attraction)方法[6-7]被用于安全包线的确定，但是ROA方法主要是基于Lyapunov能量函数[8]确定包线，函数的确定方法本身存在较强的保守性。Zheng等[9]提出了基于流形理论将飞行系统在特定飞行状态下的稳定域作为飞行安全包线，该方法虽然得到了较为精确的飞行系统的安全包线，但该方法主要是基于飞机的动力学特性确定包线，对模型的精度要求较高，因此也很难被工程应用。国内外在对于可达集方法确定安全包线上也进行了大量研究[10-13]，其中可达集的确定主要基于Mitchell的水平集工具箱[14]。但这些研究大多只是确定了飞行器完成机动动作的安全包线，并没有在操纵策略上有具体的研究，特别是对于着陆阶段的研究较少。

结冰会导致飞行安全包线收缩虽然已是业界共识，但国内外对如何确定结冰时安全包线的研究较少且局限性较大[15-17]。本文基于可达集理论，提出了将正向可达集与反向可达集的交集作为安全集，即飞行安全包线，并将其应用于结冰飞机着陆阶段。可达集的确定是基于水平集方法计算Hamilton-Jacobi方程的最优解，具体求最优解的过程采用了最优控制的方法。其中反向可达集的计算是在最优控制作用下从选定的初始集出发，计算能到达目标集的集合。另外飞机着陆时其飞行状态不可能一直能保证从初始状态开始按照预定轨道到达目标集，当遇到突发状况时，可以通过从初始状态出发计算正向可达集，这样又能重新找到新的安全初始状态。在着陆阶段，安全的着陆过程也被定义为能从初始状态安全到达指定目标状态的过程，飞行安全包线作为正向可达集和反向可达集的交集，只要使飞行状态永远保持在安全包线以内，就能保证飞机安全着陆。本文以NASA的项目飞机GTM(Generic Transport Model))作为背景飞机，通过对飞机的气动参数进行多项式拟合，建立了结冰飞机纵向通道的动力学模型。然后分别对轻度结冰和重度结冰飞机的安全包线进行了确定。最后以安全包线作为飞行安全的评价标准，对具体的飞机着陆过程进行了试验仿真验证，并提出了相应的操纵策略。

1 结冰飞机非线性模型建立

结冰会破坏飞机的动力学特性，导致升力减小、阻力增大，同时失速迎角也会大幅减小，如图1 所示，图中：CL为升力系数，α为迎角。因此飞行安全包线也会发生明显变化，为了确定结冰后的安全包线，首先应该建立结冰飞机的动力学模型。

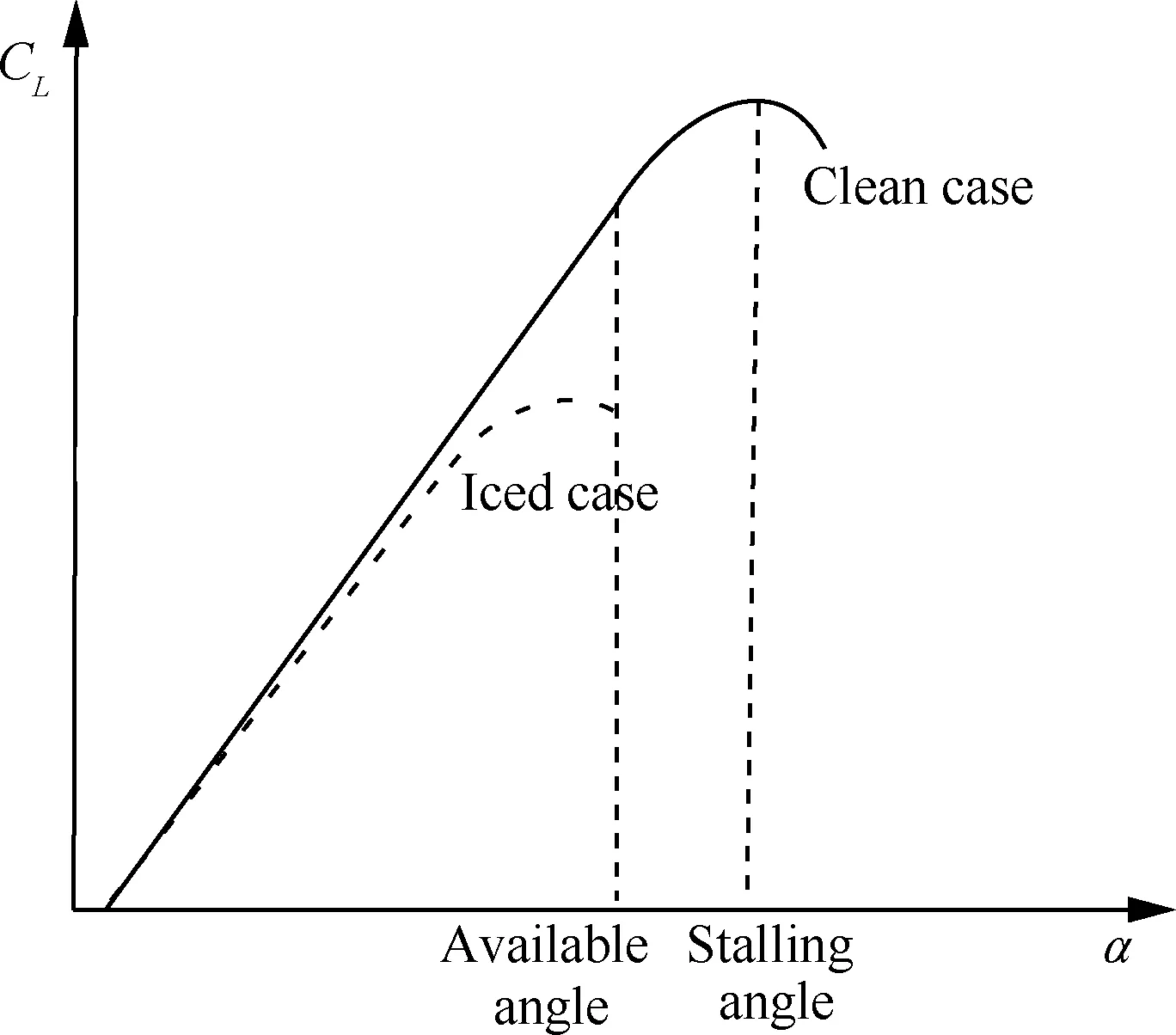
图1 结冰前后升力系数变化示意图Fig.1 Sketch map of variation of lift coefficient of aircraft before and after icing

结冰飞机着陆阶段飞行安全包线变化的过程中，通常飞机刚体模型主要包含6个自由度，但飞机在着陆阶段主要是针对纵向通道进行控制，因此本文不考虑飞机横侧向通道的状态参数变化；另外本文所涉及的控制是对飞行系统进行外环控制，不考虑飞机系统内环控制的影响，因此假定驾驶员的操纵将直接改变迎角，不考虑飞机自身的转动特性[11,18]。本文研究的模型简化为如下形式。

1.1 纵向通道飞机动力学模型建立

本文采用的结冰飞机非线性动力学方程为

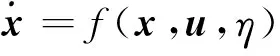
(1)

式中:状态变量x中包含飞行速度V，航迹倾角γ和高度H；控制量u由推力T和迎角α组成；η作为结冰因子表示飞机的结冰程度。建立的飞机三维非线性动力学模型表示为

(2)

式中:m为飞机质量;L为升力;D为阻力。升力和阻力可以表示为

(3)

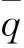
1.2 结冰飞机多项式系数模型建立

通过对飞行数据进行参数拟合[20]能够得到气动数据随迎角α、俯仰角速度q以及升降舵偏角δe变化的精确的多项式形式的解析表达式，具体表达式为

(4)

式中：多项式系数xi(i=1,2,3,4)和zi(i=1,2,3,4)是结冰因子η的函数，文献[1]指出，可通过式(5)体现结冰程度对飞机气动特性的影响。

C(A)iced=(1+ηKC(A))C(A)

(5)

式中：KC(A)用于表示结冰后飞行参数的变化，对于特定的飞机通常为常数；C(A)为结冰前力或力矩系数。结冰因子η作为一个时变量，随着结冰程度的加剧，从0到ηmax变化。其中η=0表示飞机无结冰，η=ηmax表示飞机已经完全结冰。

2 安全包线确定

飞行安全包线对于保障飞行安全尤为重要，传统的包线主要是对飞行姿态加以限制，并认为只要不超过限制就能确保安全。但是传统方法却不适用于因环境因素引起的变化，特别是结冰导致的飞机机体结构变化，而基于可达集理论确定的飞行安全包线能够解决这一问题。下面针对可达集理论计算安全包线进行具体介绍。

2.1 安全集定义

可达集的概念可表示为从初始集出发在某个控制作用下在一定时间内到达目标集的过程。对于飞机着陆来说就是在飞控系统或驾驶员作用下从着陆的初始状态到达预定的目标状态的过程。在数学上飞机的动态特性可以表示为

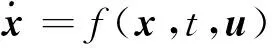
(6)

式中：x∈Rn为n维状态空间;t为时间；u∈U为控制量。其中f:Rn×[0,T]×U→Rn有界且为Lipschitz连续。状态轨迹可以定义为ξx0,t0,u(·)(t):t→x∈Rn，其中x0代表在时间t=t0时的状态，u(·)为此时的控制输入。初始集和目标集分别表示为I,Γ∈Rn。

正向可达集可定义为在时间t0从初始集出发在时间t处到达的状态集合，而反向可达集定义为从时间t出发在时间tf时到达目标集的状态集合，数学表达式为

正向可达集：

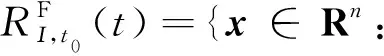
[Ι,U]|ξx0,t0,u(·)(t)=x}

反向可达集：

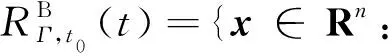
本文的研究主要是为了确保结冰飞机能在控制作用下安全着陆，反向可达集虽然理论上总能保证飞机在一定时间内通过某个控制从初始集到达目标集，但是其中的某些状态点可能会超出飞机本身的限制(如飞行速度低于失速速度，迎角大于失速迎角等)。特别是对于着陆阶段，飞行状态不可能一直保证从初始状态开始按照预定轨道到达目标集，飞机为了便于进行状态切换，必须不断地寻找新的状态点，甚至反向寻找新的合适的初始状态，这样就需要计算正向可达集。因此本文将正向可达集与反向可达集的交集作为安全集，安全集也定义为飞行安全包线，在安全包线内飞机能够通过可达集算法中的最优控制方法进行任意的状态切换，从而实现飞机的安全着陆。安全集如图2所示。图中绿色部分为正向可达集，红色部分为反向可达集，黄色部分为初始集，而安全集为绿色与红色相交部分。

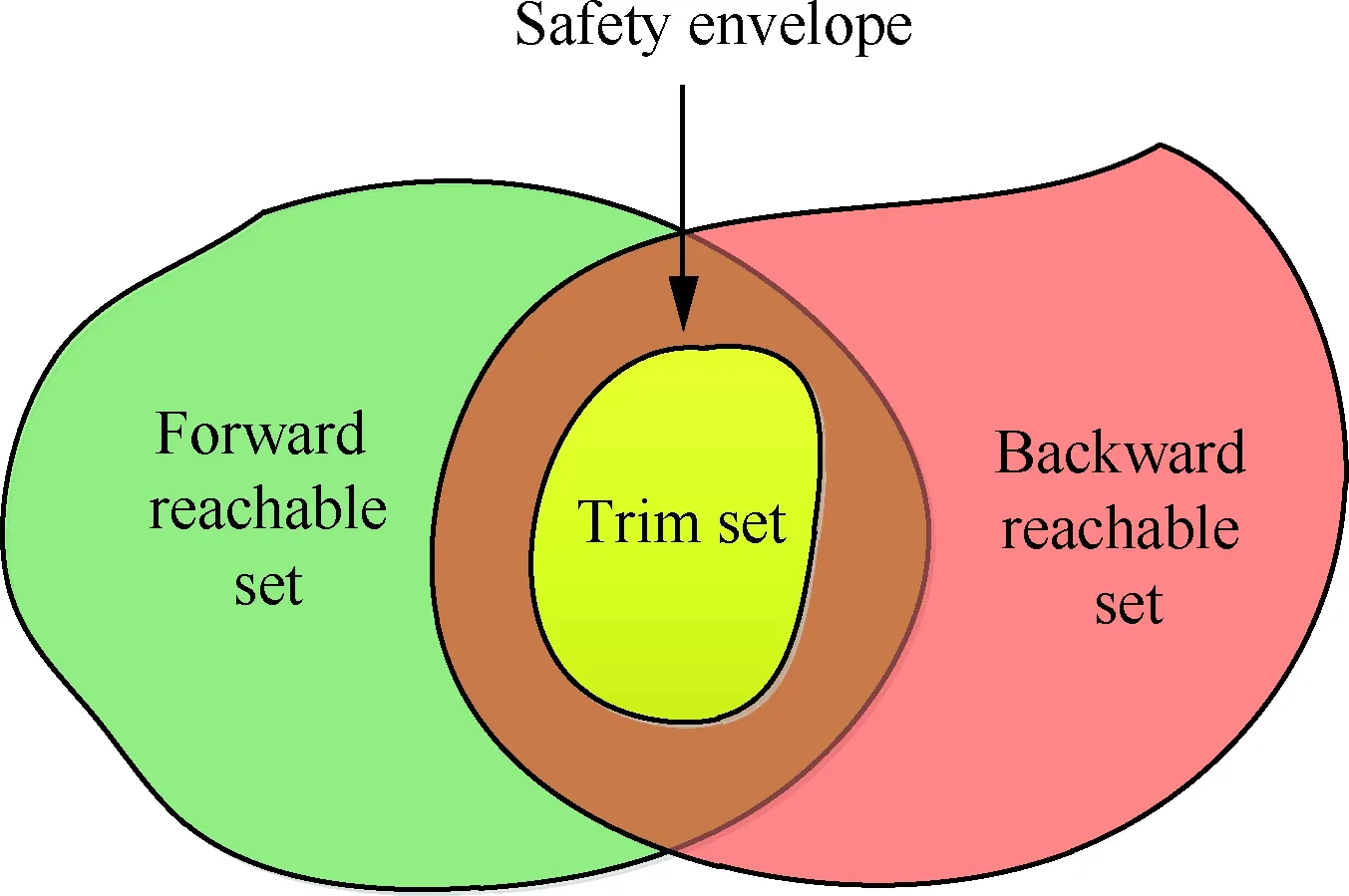
图2 安全集示意图Fig.2 Sketch map of safety sets

2.2 水平集方法

目标集和可达集都可由水平集方法表示，水平集方法是一种用于跟踪界面移动，计算隐式曲面演变的数值方法[21]。其基本思想是把低维动态曲线当作零水平集，然后将其扩充到高维水平集函数上，通过求解满足水平集函数的发展方程，推进水平集演化，此时零水平集也在不断演化，当演化趋于平稳就得到界面的形状。水平集方程可以表示为

(7)

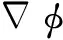
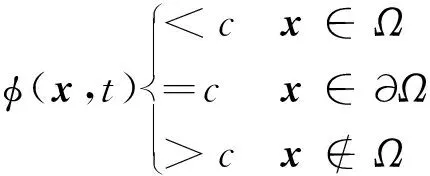
(8)

式中：Ω∈Rn表示一个有界的开区域，∂Ω∈Rn表示其边界。当c=0时，目标集和可达集的边界可由式(8)中的零水平集函数表示[22]。目标集可表示为

Γ={x∈Rn|φ(x,0)≤0}

(9)

可达集可以通过解如下的Hamilton-Jacobi方程得到：

(10)

式中：

(11)

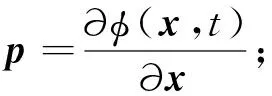
(12)

对于函数φ(x,t)，可达集的隐式表达式为

R(t)={x∈Rn|φ(x,t)≤0}

(13)

从式(11)和式(12)可知，哈密尔顿方程H(x,p)的最大值是通过最优控制u*(x,p)得到，下面介绍如何得到最优控制。

2.3 计算最优控制输入

最优控制u*(x,p)代表在某一个状态x下能使哈密尔顿方程H(x,p)达到最大的控制。最优控制输入u*(x,p)的物理意义可表示为：在控制u*(x,p)的作用下，从初始状态x出发的轨迹始终能保持在可达集内部并最终到达目标集。通常求解最优控制输入的过程是一个非凸最优化问题，需要对整个域空间进行搜索，得到能使哈密尔顿方程达到最大的控制。

对于式(1)的方程，迎角α和推力T被作为控制变量。因此最优控制输入的计算可转化为求解使H(x,p)达到最大的迎角α和推力T的组合。对于本文的模型，可以简化为求系统的最优解问题，过程如下：

结合式(2)和式(11)，令

(14)

式中：p1和p2为p的分量。

对于最优控制输入，在迎角处求偏导，得到

(15)

对式(15)进行分析，能使式(14)取最大值的最优控制如下：

1)当α*=αmin，若p1>0，T*=Tmax；若p1<0，T*=Tmin。

2)当α*=αmax，若p1cosαmax+(p2/V)sinαmax>0，T*=Tmax；若p1cosαmax+(p2/V)sinαmax<0，T*=Tmin。

3)当T*=Tmin，若p1>0，α*=αmax，0或α1；若p1<0，α*=αmax，0。

4)当T*=Tmax，若p1<0，p2>0，α*=αmax；若p1>0，p2<0，α*=0；若p1<0，p2<0，α*=αmax，0；若p1>0，p2>0，α*=0，α2。

其中α1和α2为解式(15)得到的极值点。对以上控制输入进行分析可知，要使Hamilton-Jacobi方程达到最大的控制输入可以从以下的6个组合内得到：

(αmin，Tmin),(αmin，Tmax),(αmax，Tmax),(αmax，Tmin),(α1，Tmax),(α2，Tmax)。

3 着陆阶段安全分析

本文的案例模型主要参考的是GTM纵向通道模型，在本节中首先基于可达集理论确定飞行安全包线，然后分别研究了襟翼和结冰对安全包线的影响，最后通过对具体的着陆阶段进行时域仿真分析，提出了不同结冰条件下的驾驶员应对策略。

3.1 襟翼对安全包线的影响

由于襟翼与着陆过程密切相关，因此本节对襟翼的影响进行具体的分析。襟翼偏角δ通常是从0°到最大值之间变化，本节把襟翼偏角划分为3个卡位：0°、15°和30°，针对不同卡位计算了相应的升力和阻力。升力和阻力系数曲线分别见图3和图4。从图中可看出，随着襟翼偏角的增大，升力和阻力都会相应提高。

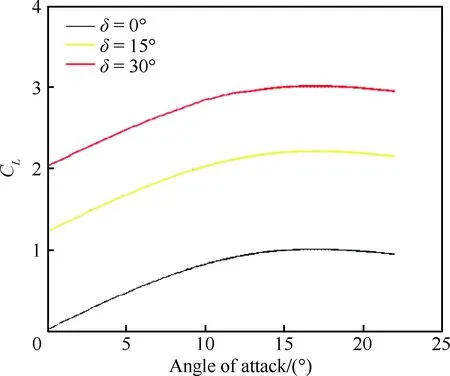
图3 不同襟翼偏角下的升力系数Fig.3 Lift coefficients for different flap deflections

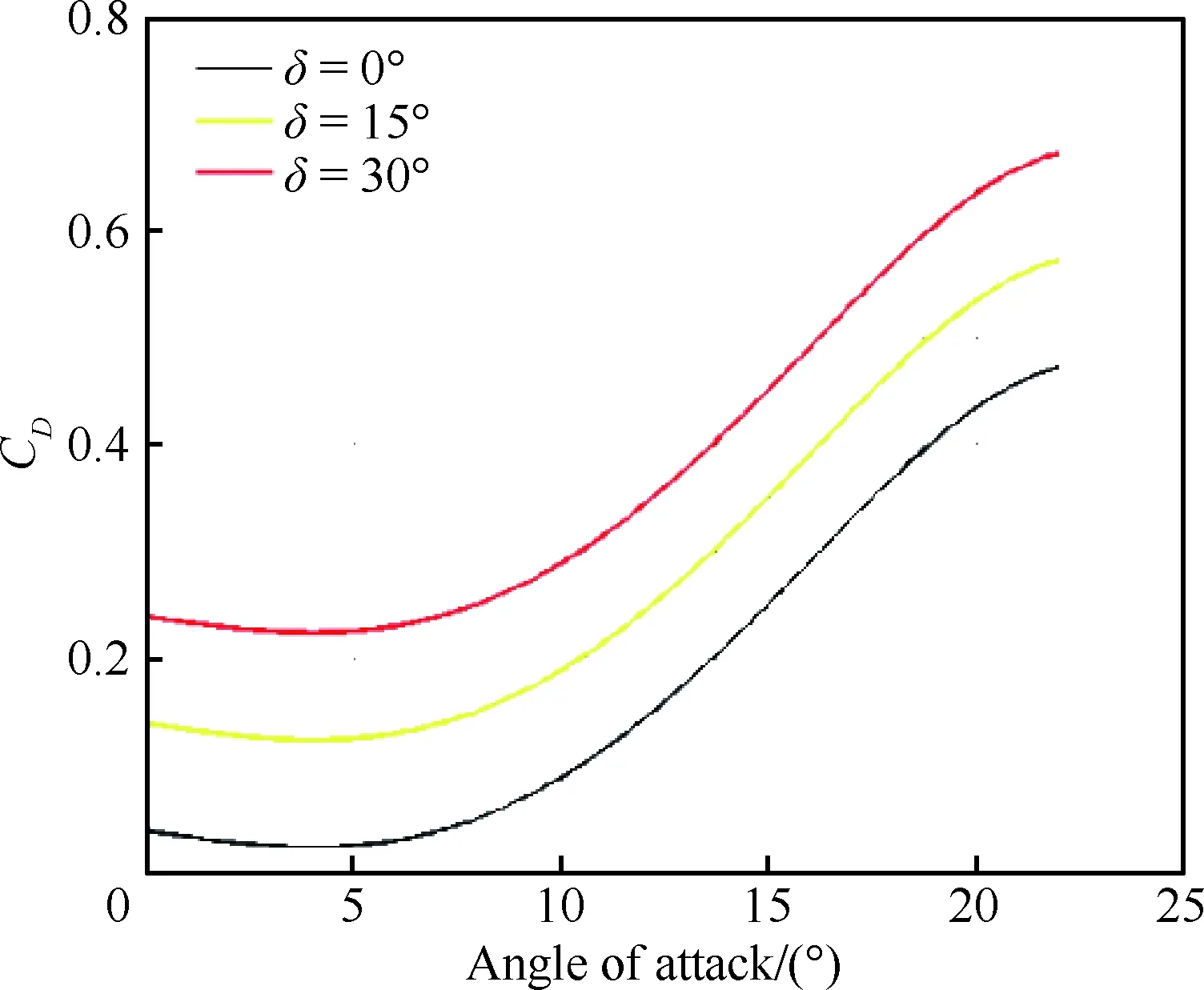
图4 不同襟翼偏角下的阻力系数Fig.4 Drag coefficients for different flap deflections

对于飞机而言，失速速度可表示为

(16)

式中：CLmax为最大升力系数，为了保证安全，适航标准要求飞机在着陆阶段的最小飞行速度不小于1.23VSR(基准失速速度)。这意味着在某个时刻如果飞机的飞行速度低于1.23VSR，其飞行状态很可能在安全包线以外，本文采用的GTM在不同卡位下的飞行参数限制如表1所示。

表1 GTM在不同襟翼偏角下的飞行参数限制Table 1 Flight parameter limitation ofGTM under different flap deflections

表1中：Vmin、Vmax、γmin和γmax分别为在计算飞机着陆阶段可达集时给出的飞行参数约束，并将这些约束作为初始集。其中Vmin的选取标准是使其至少大于1.23VSR，Vmax为根据着陆情况给定的一个最大安全初始速度。从表中可看出最大升力系数随着襟翼偏角的增大而增大，而飞机的失速速度随之减小。不同卡位下的可达集如图5所示。图5中蓝色区域和红色区域分别表示正向可达集与反向可达集，通过对图5分析可知可达集随着襟翼偏角的增大而增大。

图6为不同卡位(δ=0°，15°，30°)下的飞行安全包线，分别由黑色、红色、黄色区域表示。对着陆阶段而言，增大襟翼偏角能够提升飞机升力，从而减小失速速度，这样就能确保飞机着陆时拥有一个更大的可操纵的速度范围，安全包线也因此增大，因此增大襟翼偏角在一定程度上有助于提升飞行安全。

3.2 结冰对安全包线的影响

按3.1节的分析，襟翼对于提升着陆安全有积极作用。因此，下面对结冰影响的分析是在保证着陆时襟翼偏角为15°的条件下进行的。在区分结冰严重程度上课题组在先前已经进行了一定的研究，本文主要参照的是文献[16]中的结冰程度区分标准，即随着结冰程度加剧(结冰因子不断变大)，系统工作点的稳定性质会发生变化，最终将工作点由稳定变为不稳定时的结冰因子定义成重度结冰。因此针对本文所采用的飞机模型，提出了将η=0.1定义为轻度结冰，η=0.2定义为重度结冰。不同结冰条件下的升力系数拟合曲线如图7所示。其中黑线、黄线、红线分别表示的是无结冰(η=0)、轻度结冰(η=0.1)、严重结冰(η=0.2)时的升力系数曲线。对图7分析可知，当结冰趋于严重时，失速迎角将会快速减小。

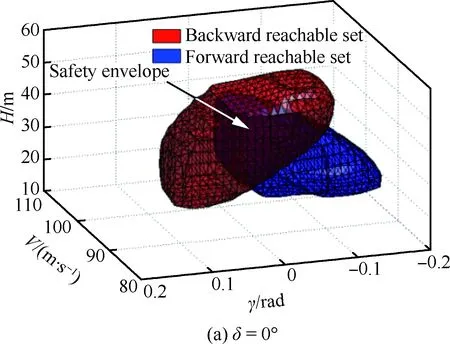
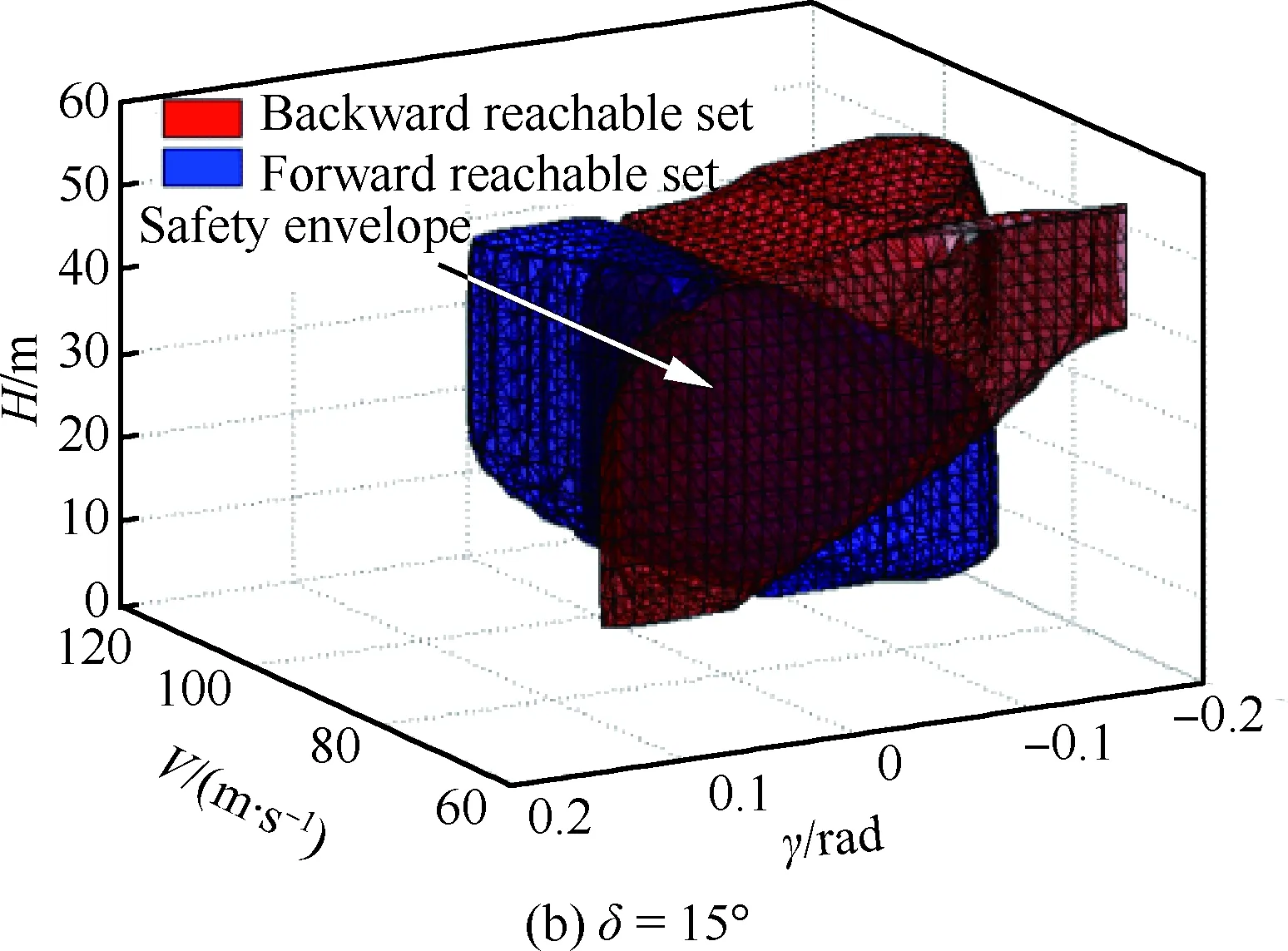
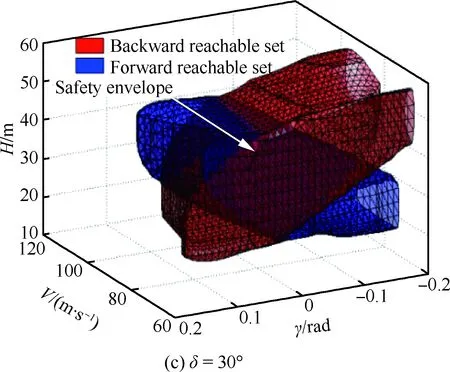
图5 不同卡位下的可达集(δ=0°，15°，30°)Fig.5 Reachable sets for different modes (δ=0°, 15° and 30°)

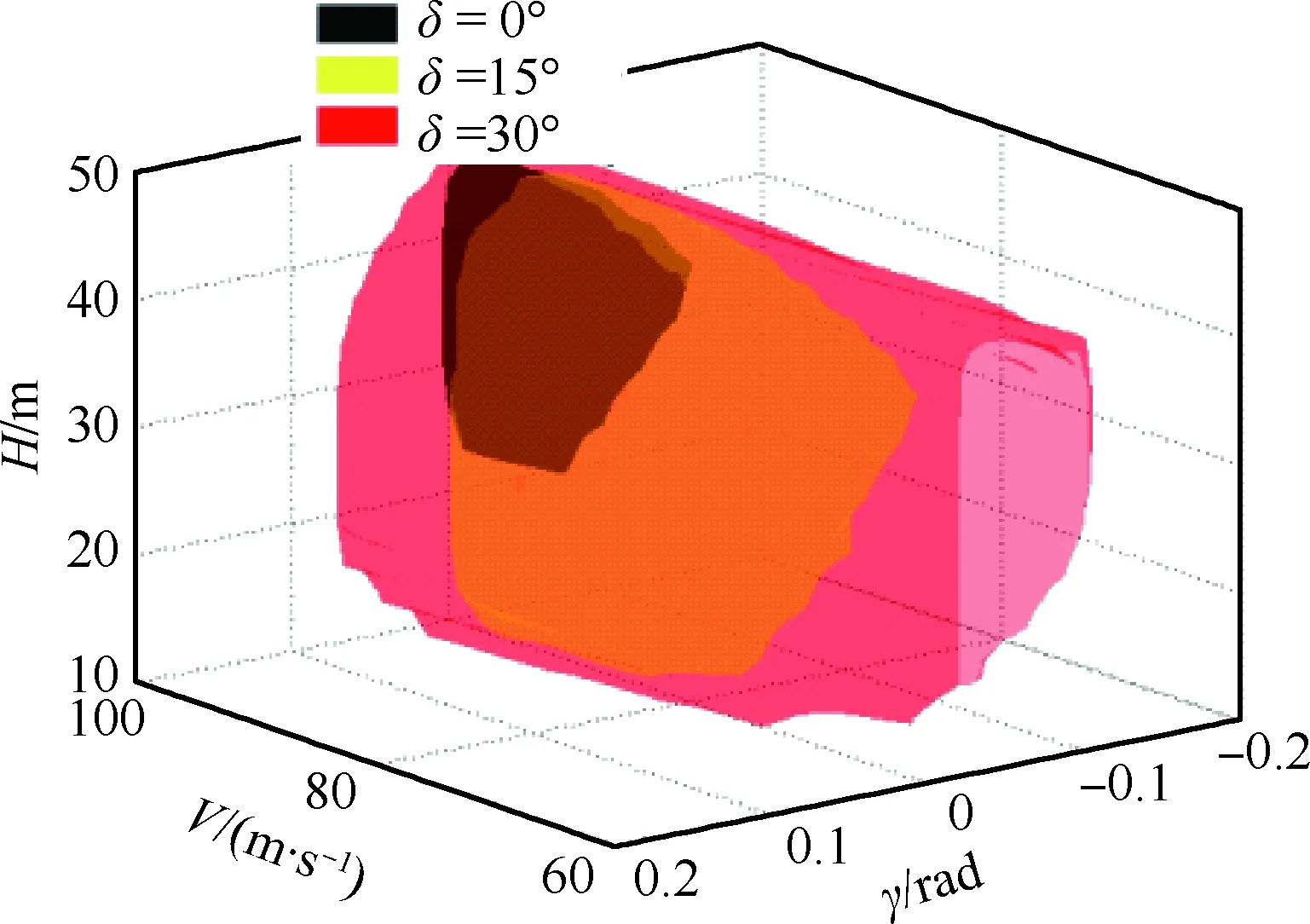
图6 不同卡位下的飞行安全包线(δ=0°,15°，30°)Fig.6 Flight safety envelopes for different modes (δ=0°, 15° and 30°)

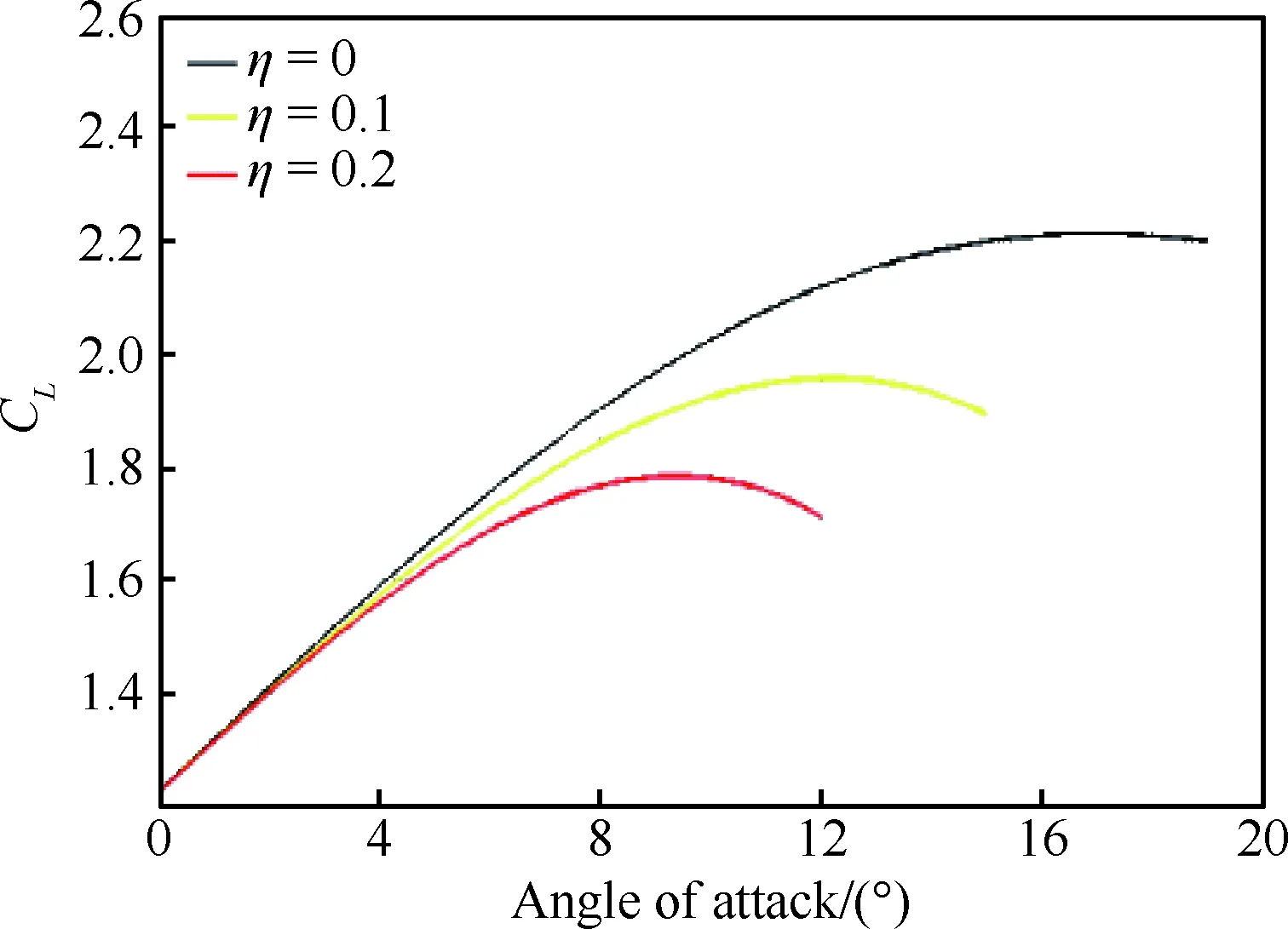
图7 不同结冰程度下的升力系数Fig.7 Lift coefficients of different degrees of icing

结冰程度增大，最大升力系数随之减小，失速速度也将发生变化，GTM在不同结冰程度下的飞行参数限制如表2所示。

表2 GTM在不同结冰程度下的飞行参数限制Table 2 Flight parameter limitation of GTMunder different degrees of icing

对于着陆阶段，失速速度随着结冰程度增加而变大，这使得飞机很难达到安全的着陆状态范围，因此，此时的飞行包线也将减小。图8描绘了在不同结冰程度下的飞行安全包线变化(η=0,0.1，0.2)，分别由红色、黄色、黑色区域表示。对于轻度结冰(η=0.1)，安全着陆速度能到达75 m/s，这能够保证飞机以正常方式安全着陆。此时，驾驶员仍能够通过正常操纵使飞行状态维持在安全包线以内。对于严重结冰(η=0.2)，安全包线收缩严重，安全着陆速度范围也随之减小，能保证安全着陆的最小速度已经超过80 m/s，驾驶员已经很难在最优控制指导下找到安全的着陆轨迹。此时对于驾驶员操纵已经非常困难，着陆风险也随之增加。因此驾驶员要改变操纵行为，只有当结冰处理后才能继续着陆。

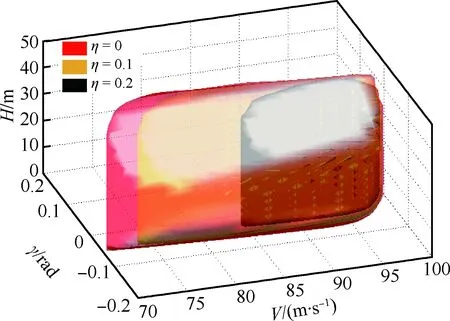
图8 不同结冰程度下的飞行安全包线Fig.8 Flight safety envelope affected by degree of icing

3.3 驾驶员操纵策略时域仿真

本节主要是针对不同的结冰程度提出相应的操纵策略并对其进行时域仿真验证。对于轻度结冰，时域仿真从状态点A(V=91 m/s，γ=-0.034 9 rad,H=40 m)开始到达终点B(V=75 m/s，γ=0 rad,H=0 m)，具体见图9。红色和黄色区域分别代表无结冰和轻度结冰时安全包线，黑线代表最优控制下的着陆轨迹，这条轨迹能始终保持在安全包线以内。这表示轻度结冰程度下，飞机仍然能够通过最优控制方法至少找到一种控制使飞机安全着陆。从而验证了轻度结冰条件下驾驶员仍然能够通过正常操纵安全着陆。

图9 轻度结冰条件下着陆轨迹Fig.9 Landing trajectory in mild icing condition

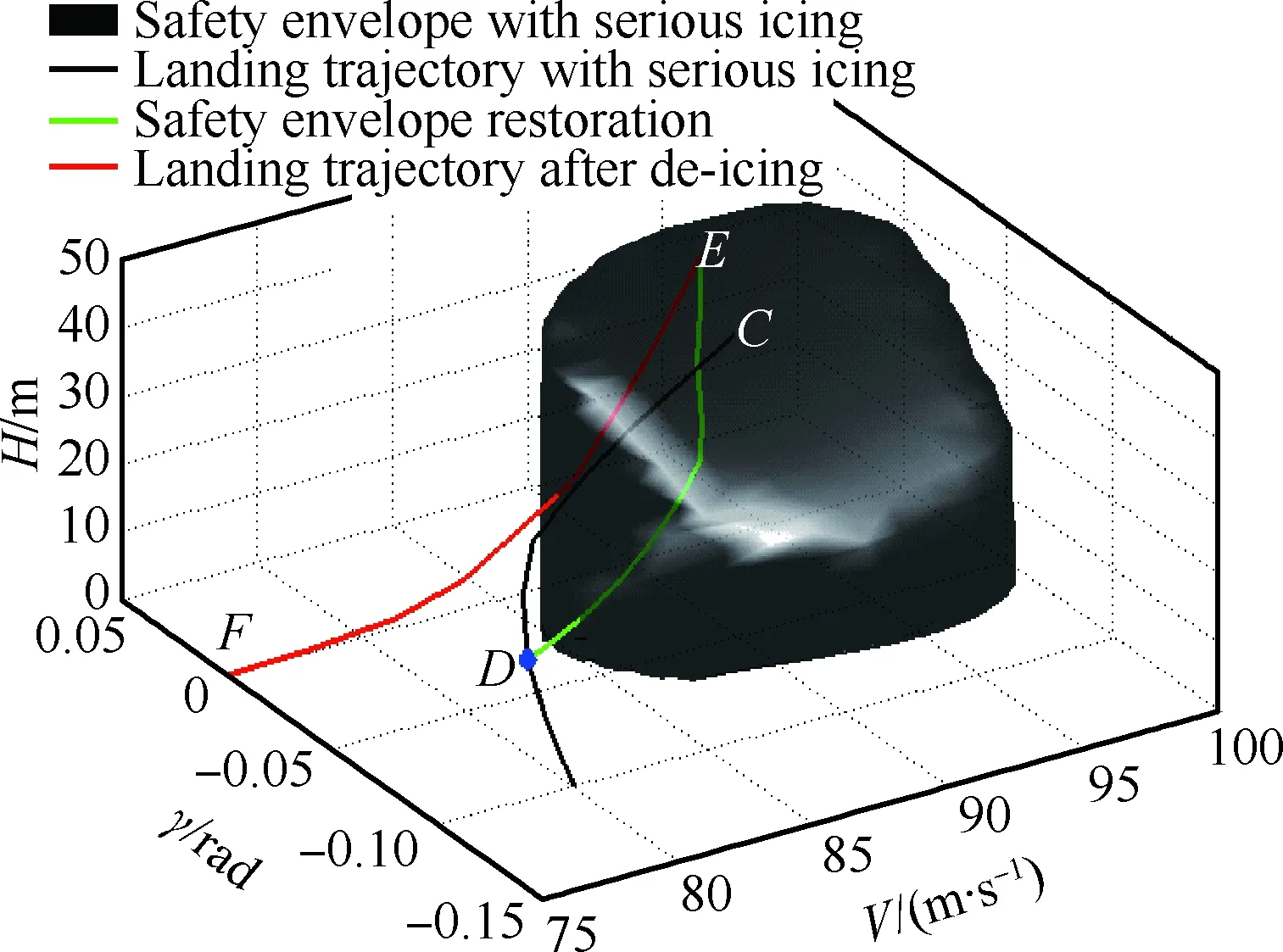
图10 严重结冰条件下着陆轨迹Fig.10 Landing trajectory in serious icing condition

对于严重结冰，从初始点C(V=90.77 m/s，γ=-0.044 9 rad,H=41.39 m)处进行时域仿真，具体如图10所示。黑色曲线代表驾驶员未觉察到结冰时，正常操纵下飞机的着陆轨迹。从图中可看出，在严重结冰时，飞行安全包线已经收缩严重，此时已经很难找到一种控制使飞机仍然能够保持在安全包线以内，如若继续着陆，飞机将会承受坠毁的风险(如黑色曲线所示)。

由前面分析可知，严重结冰时飞机应该停止继续着陆，并进行边界恢复操纵，此时可以在状态点D(V=81 m/s，γ=-0.065 rad,H=10 m)处进行边界恢复。基于最优控制理论在状态点D处先以最大推力使飞机重新起飞，然后不断调整推力T进行边界恢复，具体控制输入见图11。图10 中的绿线代表边界恢复曲线，曲线从D开始在图11的控制作用下重新回到边界内的状态点E(V=92.31 m/s，γ=0.007 2 rad,H=44.72 m)。飞机可以在点E附近进行除冰处理，当飞机结冰程度低于轻度结冰(η=0.1)时，飞机可重新进行着陆操纵。图10中的红色曲线(曲线从起点E到终点F)为飞机在除冰处理后，重新在最优控制下的着陆曲线。

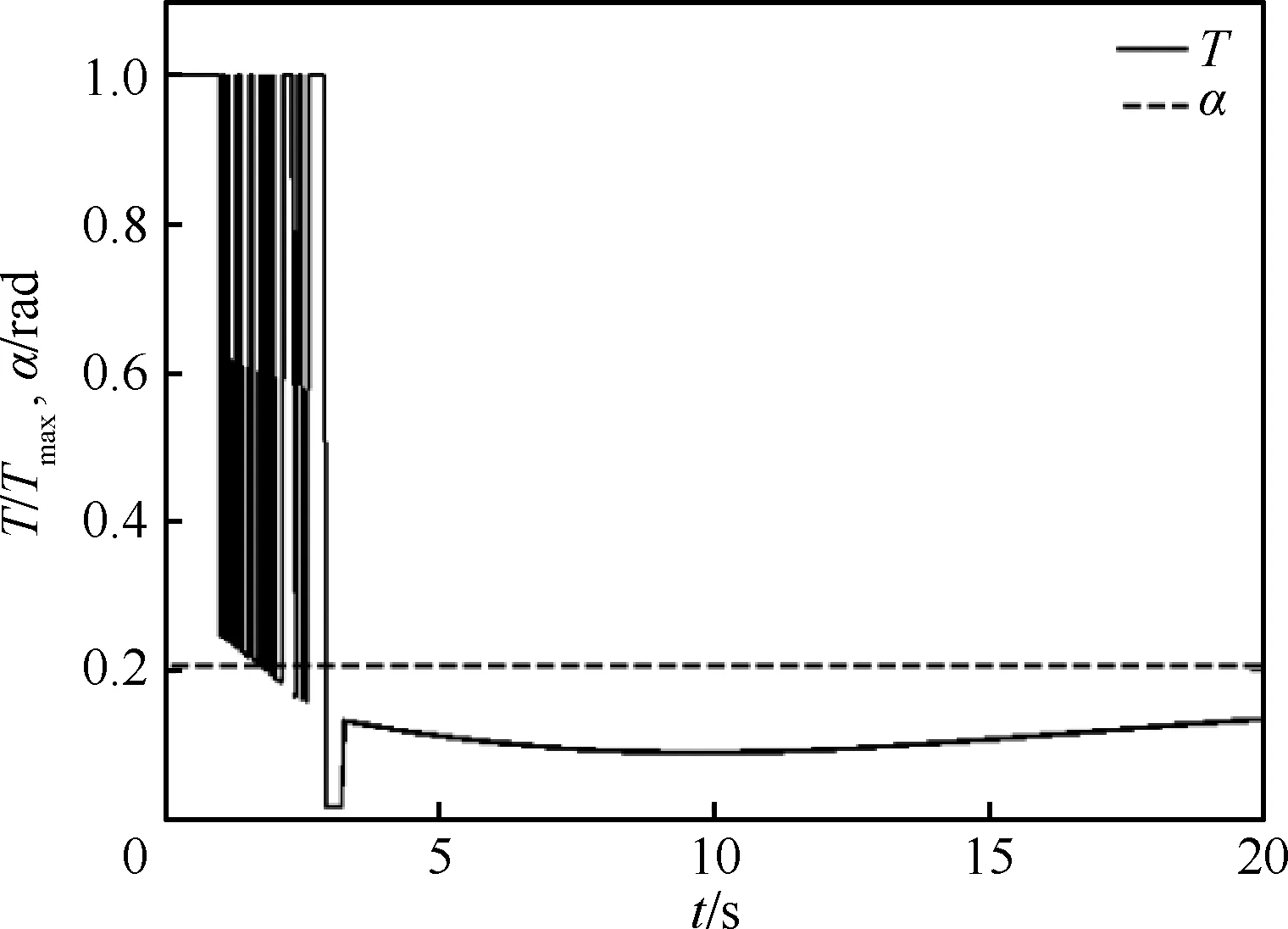
图11 最优控制输入时域响应曲线Fig.11 Time domain response curves of optimal control inputs

以上对飞行状态进行边界恢复的控制输入主要是在理想状态下(不考虑驾驶员的操纵延迟和发动机推力的响应延迟等因素)，通过最优控制使飞机由图10中飞行安全包线外的状态点D直接到达包线内的状态点E。在进入安全包线后的爬升阶段，在最优控制指导下对飞机推力的控制也在不断切换，从而出现了图11中的剧烈抖动，这种操纵输入在飞行实践中可能并不存在。前文中这样设计只是在理论上对操纵进行了实现，为了满足工程实践需求，现给出如下操纵策略(此操纵应对策略来源于前面的理论分析)。首先在状态点D处以最大推力和最优迎角快速到达包线内的状态点G，如图12所示。然后在状态点G处利用传统的驾驶员操纵方法使飞机爬升至状态点H处，其中整个爬升阶段的飞行状态都保持在安全包线以内，爬升轨迹由图中蓝线表示。具体驾驶员操纵见图13所示。最后在状态点H附近进行除冰处理，待除冰结束后，重新按照传统操纵方法进行着陆。图12中的黄色曲线表示驾驶员按照传统操纵方法实现的着陆轨迹。通过与最优控制方法所确定的安全着陆轨迹对比可知，在安全包线内，传统的驾驶员操纵方法也能使飞机安全着陆，这进一步说明了本文提出的安全包线可对结冰条件下的驾驶员操纵进行指导。

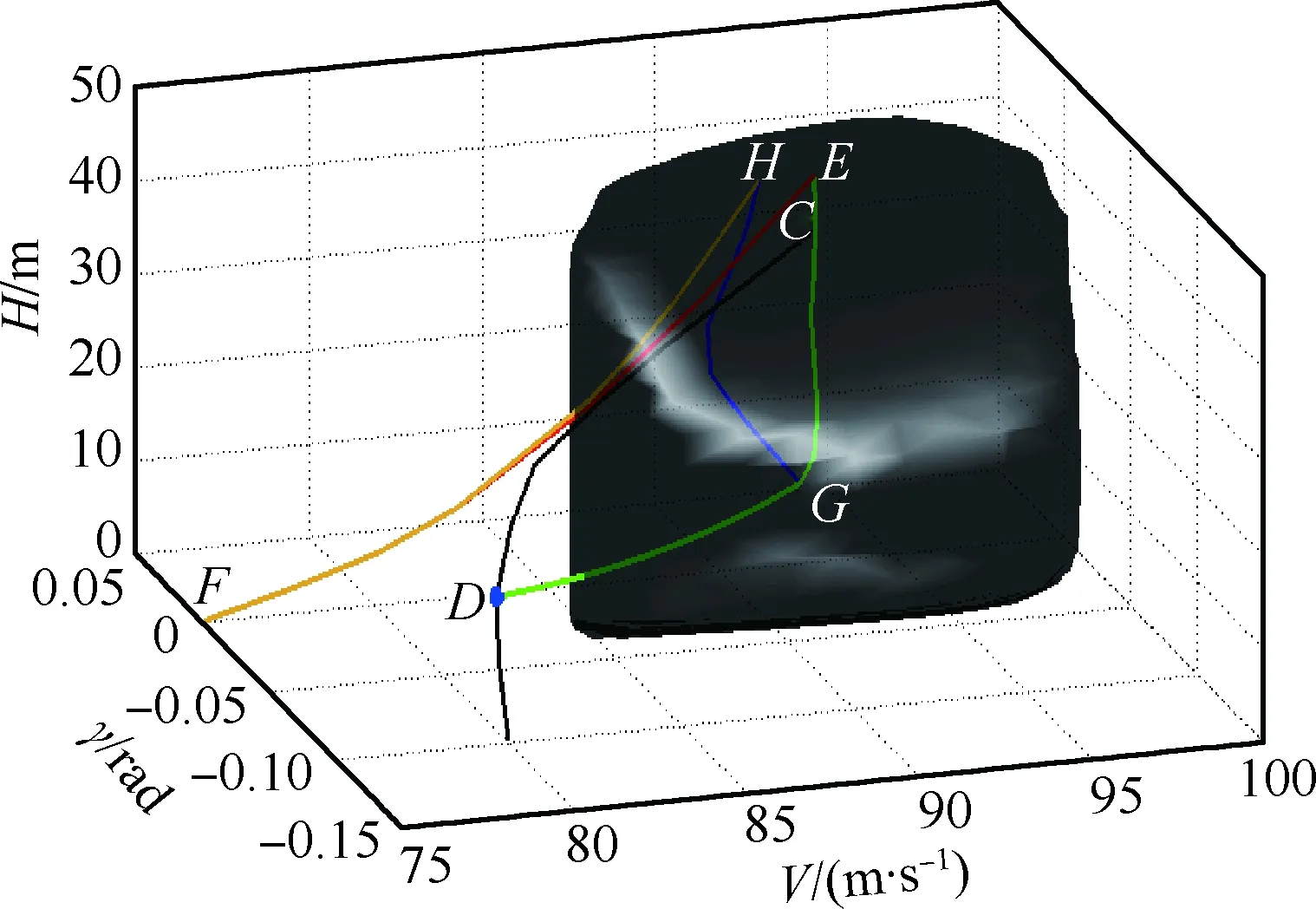
图12 最优控制与传统操纵方法着陆轨迹对比Fig.12 Comparison of landing trajectory between optimal control and traditional manipulation method

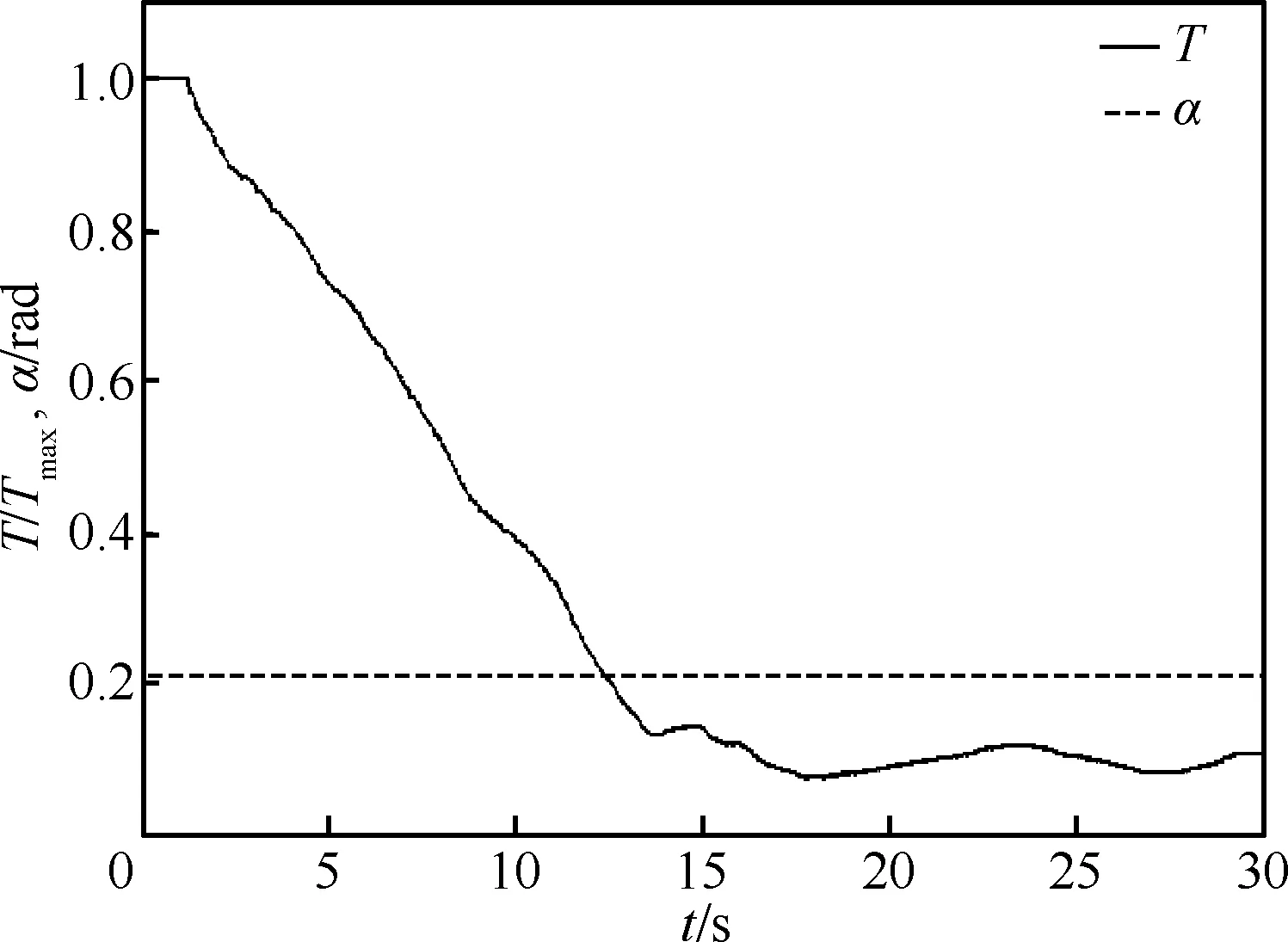
图13 传统驾驶员操纵时域响应曲线Fig.13 Time domain response curves of traditional manipulation

4 结 论

本文以GTM为研究对象，提出了基于可达集理论确定结冰飞机在着陆阶段的安全包线，通过对结冰后的飞机进行时域操纵验证，给出了在不同结冰条件下的安全操纵策略，主要成果如下：

1) 驾驶员在未察觉到结冰时操纵极易使飞行状态超出安全包线，基于可达集理论确定的安全包线能够突破传统包线的限制，适用于不同程度的结冰条件安全性分析。

2) 将正向可达集与反向可达集的交集作为飞行安全包线，可以确保飞行状态能始终在最优控制下保持在安全包线之内，这对于确保着陆安全具有重要意义。

3) 不同程度的结冰条件应给出不同的应对策略。对于轻度结冰，在飞行包线内仍然能通过最优控制使飞机安全着陆。而对于严重结冰，飞行包线收缩严重，常规操纵已经很难保证飞机继续安全着陆，此时必须在着陆轨迹的某个状态点处进行边界恢复操纵，使飞行状态重新回到安全包线内，待除冰完成后再继续进行着陆。