基于射线追踪的快速雷达图像仿真方法

谢志杰，岳 慧，袁黎明，应小俊

(上海航天技术研究院 电磁散射重点实验室,上海 200438)

0 引言

随着高分辨雷达卫星(如TerraSAR-X)的投入应用，合成孔径雷达(SAR)图像的方位向和斜距向分辨率达到1 m[1]。雷达分辨率的提升，以及雷达图像日趋复杂，对雷达图像解译的需求日益增加。同时，目标识别所需的先验数据，以及隐身目标设计等，同样对雷达图像提出了大量需求。因此，本文提出了一种基于射线追踪(SBR)的快速雷达图像仿真方法。

SBR方法是由LING等[2-4]提出的用于计算腔体和由多种复杂部件组合而成的电大尺寸目标雷达散射截面(RCS)的高频近似方法。SBR方法分为射线追踪、场强追踪和远场积分3个步骤。

本文提出了一种基于SBR的快速雷达图像仿真方法。该方法利用射线来模拟电磁波对目标的入射[5]，对每一条射线在雷达成像平面内的投影坐标进行求解；之后利用场强追踪模块来求解射线管的出射场强；最后对所有射线管的贡献在图像域进行累加，并通过加窗处理得到1幅雷达图像。通过对具有不同传播路径的射线进行聚类，可实现对散射贡献的分离，从而建立目标部件与强散射源的对应关系，并对复杂目标的散射特征和雷达图像进行解译。

1 快速雷达图像仿真方法

对基于SBR的快速雷达图像仿真方法进行介绍。

1.1 场景模拟

利用SBR求解每一条射线在雷达成像平面的投影坐标。射线追踪模块是在开源代码POV-Ray基础上改进而来的[5]。首先，定义垂直于入射方向的虚拟孔径面(等相位面)，并对虚拟孔径面进行射线管划分。对每一个射线管，分别以射线管中心为起点，入射方向为射线方向，对射线进行追踪。当与目标相交时发生反射，再对反射射线进行递归追踪直到射出目标区域。在此过程中，记录射线管的所有反射位置。

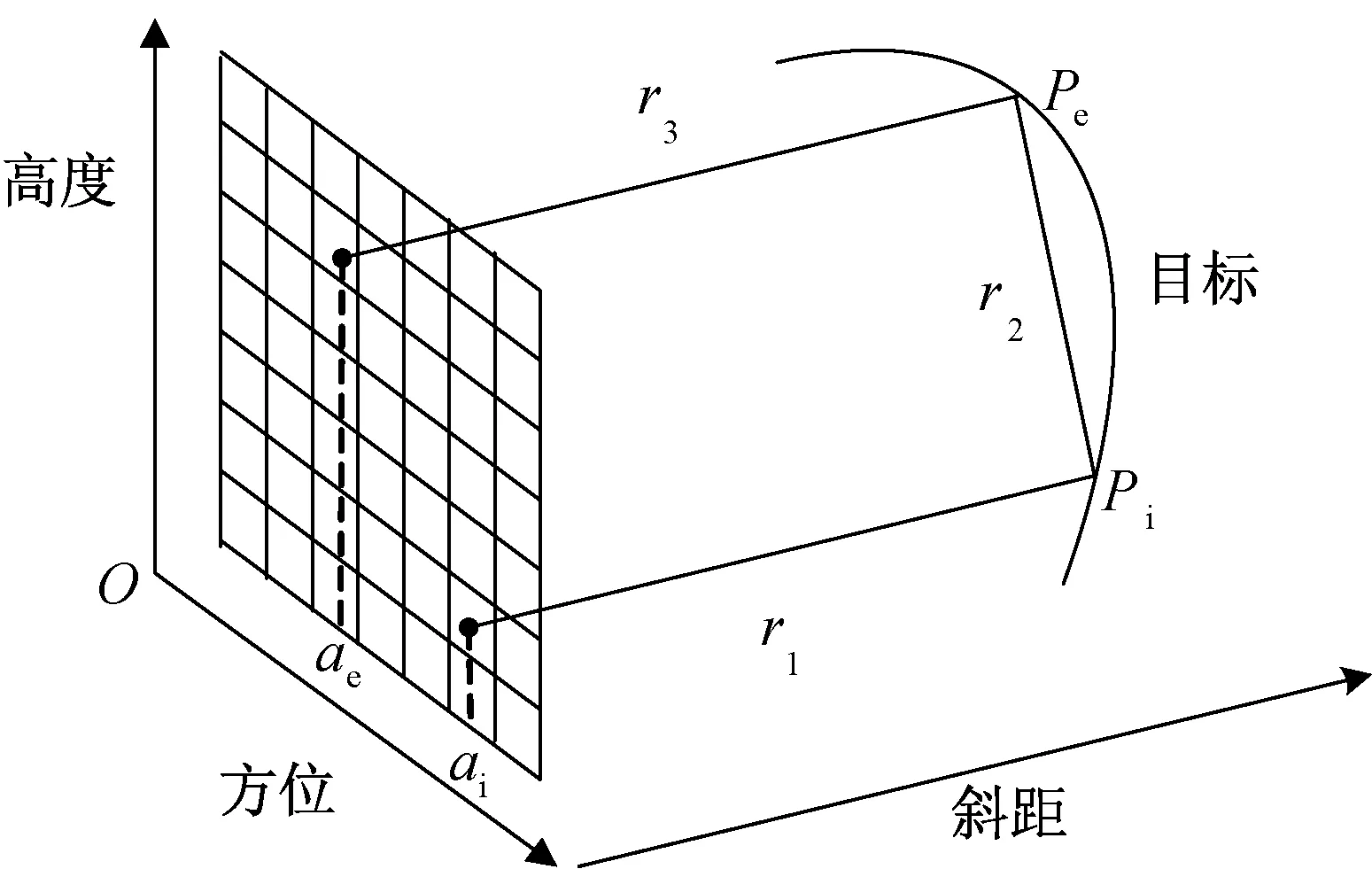
图1 射线追踪示意图Fig.1 Schematic diagram of ray tracing

射线追踪的示意如图1所示。图中：由左侧虚拟孔径面发出的射线，经过距离r1到达入射点Pi，发生反射后又经过距离r2到达出射点Pe，最后从Pe经过距离r3返回虚拟孔径面。

由雷达成像得到目标三维散射特征在雷达成像平面的二维投影。雷达成像平面有斜距向和方位向2个坐标轴。利用射线追踪机制对每一条射线在雷达成像平面上的投影坐标进行了求解。

对于每一个射线管需要分别计算其在雷达成像平面上的斜距向坐标和方位向坐标。为了计算射线管对应的斜距向坐标，对射线追踪的代码进行了修改，使其可以提取每一个反射点的深度信息，即射线从上一个反射点(或虚拟孔径面的入射点)到当前反射点的距离信息。在单次反射情况下，射线管斜距向的坐标rs直接由反射点的深度决定，即

rs=r1

(1)

对于图1所示的二次反射情况，射线管斜距向坐标为当前射线从虚拟孔径面出发直到再次返回虚拟孔径面所经过距离和的1/2，即

rs=(r1+r2+r3)/2

(2)

式中：r1，r2，r3的意义如图1所示。

对于更高次的反射，目标几何结构之间的反射射线数目增加，斜距向坐标可表示为

(3)

式中：K为射线数目，其等于当前射线的反射次数加1；rk为射线的深度。

在求解多次反射方位向坐标时，可将入射点的方位向坐标与出射点方位向坐标取平均值作为当前射线管多次反射方位向坐标，即

aa=(ai+ae)/2

(4)

式中：ai为入射点方位向坐标；ae为出射点方位向坐标。对于单次反射射线，ai=ae。

1.2 场强追踪

在场强追踪部分，对每一条射线对应的出射电场幅度矢量和相位信息进行求解。

在高频入射条件下，目标对电磁波的反射遵循几何光学原理。根据Snell反射定律及边界条件，反射电场可表示为[6-7]

(5)

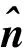
在得到最终出射点的入射电磁场之后，散射电场可利用物理光学法进行求解。在已知出射点处入射电磁场强度时，其感应电流可表示为

(6)

式中：Hi为目标表面处的入射磁场强度。射线管的散射场为

(7)

式中：Esca为射线的最终散射电场强度；Z0为自由空间的波阻抗。

在选择坐标原点为相位参考中心之后，电场相位可分几部分进行计算。入射点与出射点的示意图如图 2所示。

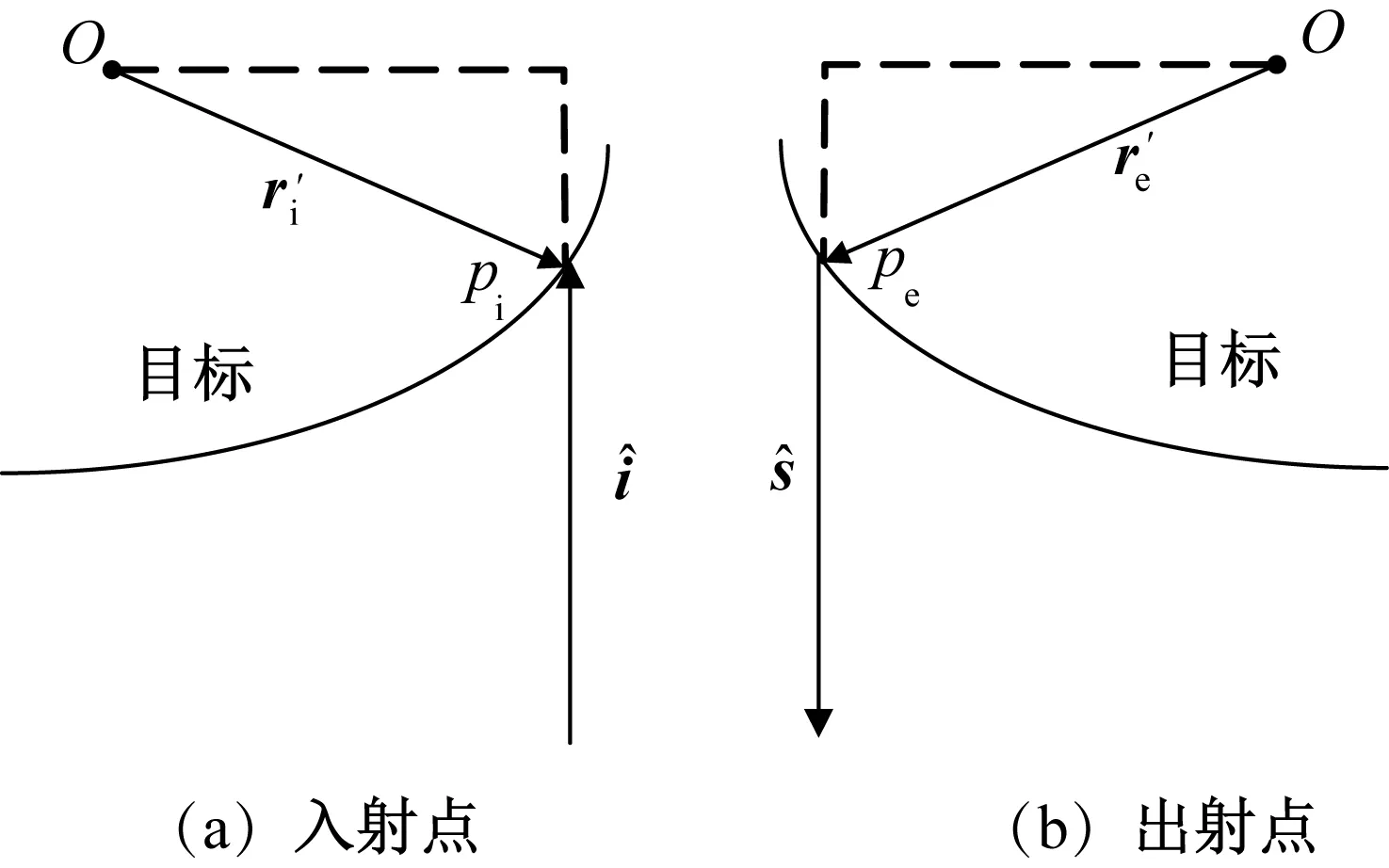
图2 入射点与出射点示意图Fig.2 Schematic diagram of incident point and exit point

对于每一条射线，由于入射点、出射点偏离相位参考中心所在的等相位面，会引入1个相位。入射点相位为

(8)

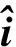
(9)

此外，射线从入射点到出射点之间的传播过程也会造成相位延时，需要添加补偿相位

pc=-l*d

(10)

式中：d为射线从入射点到出射点过程中所经过的传播距离，即入射点pi到出射点pe之间的距离，即r2(见图1)。

计算中，通过在每一条射线出射点的散射电场上乘以相位影响因子cp来表征多次反射所造成的影响，其值为

cp=ejp

(11)

式中：当前射线出射点处电场的相位p=pi+pe+pc。

1.3 快速雷达图像仿真

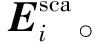
ej2k0(r-ri)δ(r-ri,a-ai)

(12)

式中：k0=2πf0/c为中心频率；Δk=2πB/c为扫频带宽；θ0为扫过角度；gi为第i条射线的散射电场；Ai为当前射线管面积。

雷达图像可通过对式(12)所得结果进行加窗处理得到，频域加窗在图像域表示为与窗函数的卷积

O(r,a)=S(r,a)*[W(Δk·r)·W(k0θ0a)]

(13)

式中：W为汉明窗的窗函数，其表达式为[8]

[D(θ-I)+D(θ+2π/I)]

(14)

式中：α为常数，通常α=0.54；D为sinc函数；I为汉明窗的点数。

快速雷达图像仿真算法避免了对每一方位和频率下的散射贡献的计算，可节省大量时间。通常，对于1个复杂目标，利用上述快速成像方法仅需几分钟即可获得1幅雷达图像。

2 仿真算例

利用本文方法对Slicy模型[9]的雷达图像进行计算。Slicy模型的几何外形如图3所示，主要由2个长方体1和2，1个1/4圆柱体3，1个角反射器4，1个实心圆柱体5，1个圆柱腔体6组合而成，x轴方向尺寸约为3 m。

图3 Slicy几何模型Fig.3 Slicy model

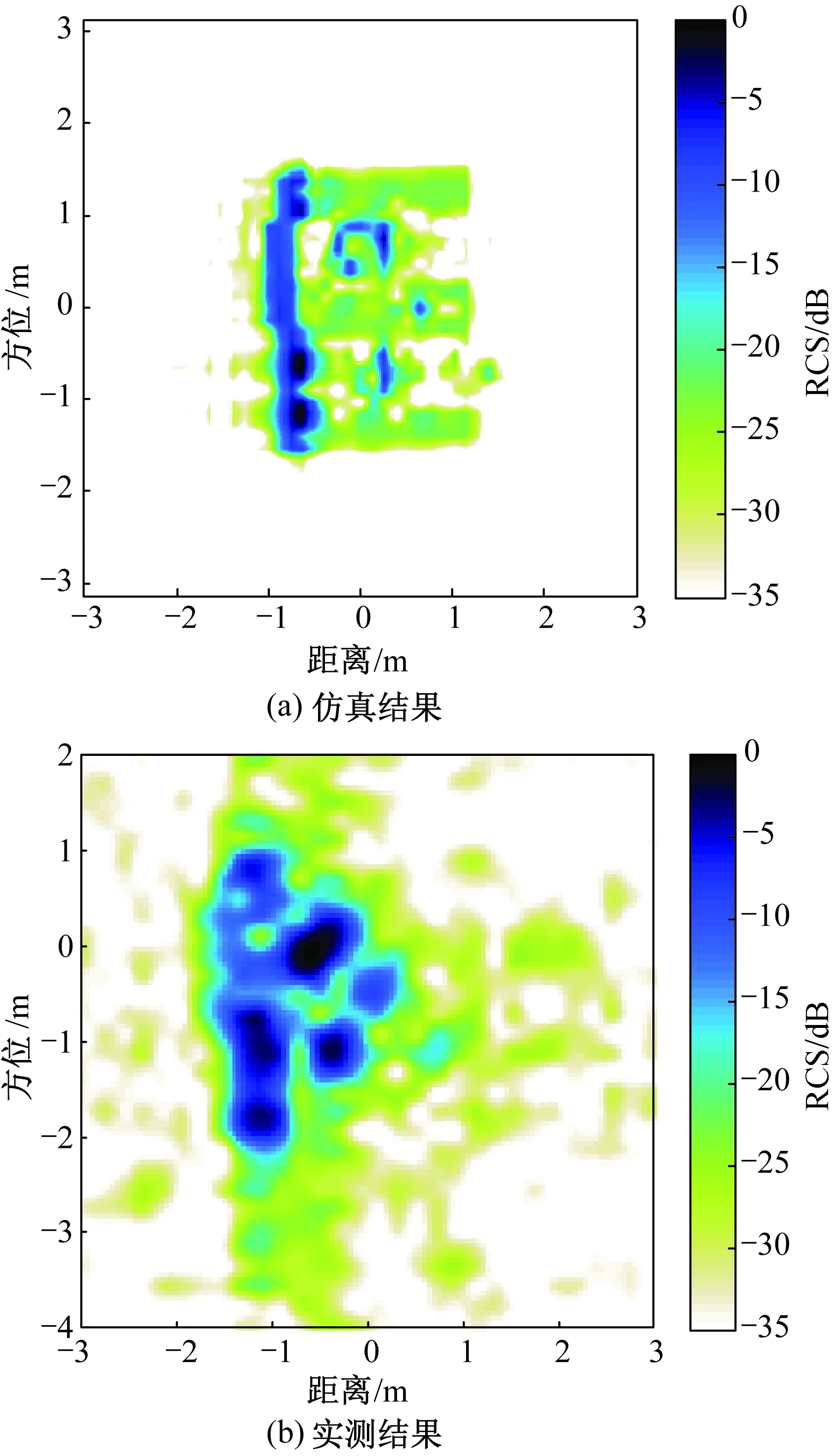
图4 Slicy模型雷达图像结果对比Fig.4 Comparison of radar images of Slicy model

当俯仰角(雷达视线与z轴的夹角)为60°、方位角(雷达视线在水平面投影与x轴的夹角)中心值为-89°、扫角宽度为4.08°、中心频率为9.599 GHz、带宽为0.591 GHz时，利用基于SBR的快速雷达图像仿真方法对Slicy模型的二维像进行计算，并将计算结果与实测数据成像结果进行对比，如图4所示，从而对本文算法进行验证。本文实测数据来源于美国国防部高级研究计划局和美国空军研究实验室联合开发的运动与静止目标的获取与识别(MSTAR)数据库[9]。

图4(a)为本文基于SBR的快速雷达图像仿真算法计算所得结果，图4(b)为MSTAR实测数据成像结果。由于实际测量中Slicy目标是放置在野外利用机载SAR进行观测，因此不可避免引入了背景。对比图4(a)和图4(b)可看到，图中各散射中心基本吻合。

为表征实测数据结果与仿真结果之间的相关性，引入归一化积相关系数[10-11]

(15)

式中：X,Y分别为图4(a)和图4(b)对应的灰度矩阵。归一化积相关系数为1时，表示2幅图像完全相同；归一化积相关系数为0时，表示2幅图像完全不相关。通过计算发现基于SBR的快速雷达图像仿真算法的计算结果与实测结果的归一化积相关系数能达到0.84。考虑到实测数据中存在较强的背景信息，已足以说明本文算法的有效性。

3 基于射线聚类的雷达图像分析

SBR方法是通过射线来模拟电磁波对目标区域的入射。所有射线集合可表示为

U={rq,q=1,2,…,Q}

(16)

式中：Q为射线的总数目；rq∈Q为Q中某条射线。

射线总集可根据传播路径不同分为数个子集，每个子集可表示为

Sj={rj1,rj2,…,rjKj}

(17)

式中：j为子集编号；Kj为该子集中的射线数目。

子集的划分可根据射线的反射次数、出射点位置等。通过对具有不同路径特点射线进行聚类，可实现散射贡献的分离，即

(18)

式中：Ork(r,a)为子集Sj中所有射线对雷达图像产生的贡献。通过这种方式可建立目标部件和散射机理与强散射中心之间的对应关系，从而可对复杂雷达图像及目标特征进行分析。

在Slicy模型仿真算例中，通过对单次反射射线和多次反射射线进行聚类，可获取2种分量所生成的雷达图像，如图5所示。图5(a)为将单次反射射线在像域的贡献进行累加得到的图像，图中显示的散射中心均为Slicy模型中各个平面或柱面单次散射造成的，由于采用斜入射，因此单次散射所形成的散射中心比较弱。图5(b)为将多次反射射线的贡献在像域进行累加得到的图像，图中各个散射中心均为多次反射造成的。图5(b)中的散射中心1为Slicy模型底座1、2形成的二面角的散射中心，散射中心2对应角反射器4，散射中心3为2个圆柱体5、6与底面之间多次反射形成的，散射中心4为2个圆柱体5、6之间多次反射造成的，散射中心5为圆柱腔体4的散射造成的。

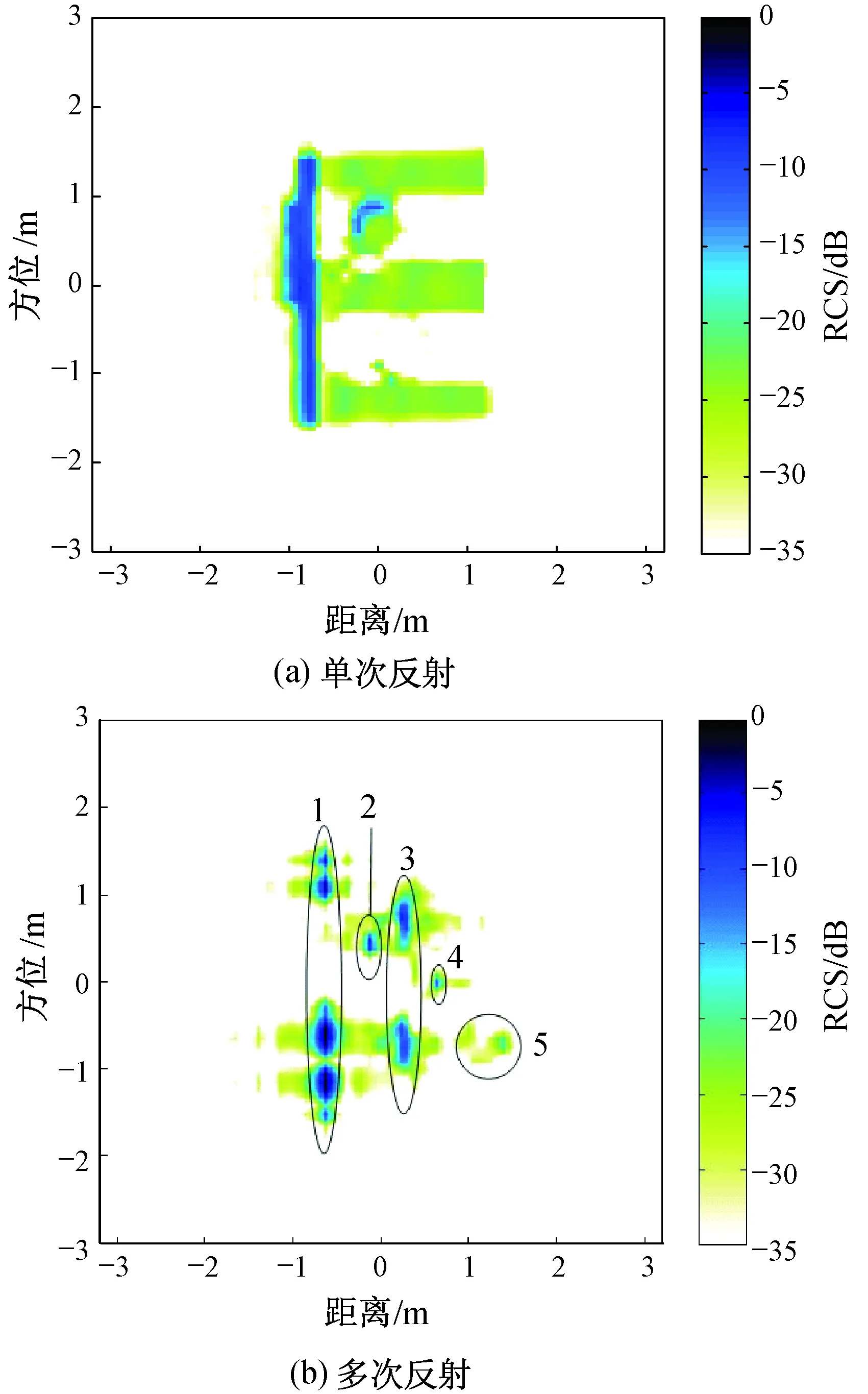
图5 分次反射的雷达图像Fig.5 Separated radar images by different ray clusters

4 结束语

本文介绍了一种基于SBR的快速雷达图像仿真方法，并利用Slicy模型的算例对该算法进行了验证。通过将射线聚类的思想引入到快速雷达图像仿真，实现了目标散射分量的分离，从而可对复杂雷达图像进行解释。后续将阻抗边界条件引入弹跳射线法，并通过对射线追踪过程进行优化与加速，从而实现对含介质复杂大场景的散射特性仿真与分析。