固本求真,追求数学课堂的深度思维
——《什么是周长》一课教学有感
浙江省义乌市教育研修院 许忠平
我们很多时候会通过概念去理解事物,可是很多时候又并未真正了解概念意味着什么。如《什么是周长》一课是属于概念教学经典课例,各种不同思路的设计版本颇多,有的基于概念的形成,有的基于概念的同化等。其实,无论采用哪种路径进行概念教学,关键在于概念本质的构建。如果能抓住最核心的本质,看事物会更精准。基于这样的思考,我进行了《什么是周长》一课的下水课,把构建概念本质和数学思维方法作为教学的重点,发展学生的思维。
一、深思慎取,操作中凸显本质
概念是反映客观事物最一般的本质属性的思维形式,正确地理解和形成一个数学概念,必须明确这个数学概念的内涵,在概念形成的过程中,抽取事物的本质属性是关键。就“周长”而言,“一周”就是其本质属性,而对于“一周”而言,学生已经有着丰富的生活经验。因此,我精心设计了两个操作活动,让学生对周长的本质属性形成初步的体验。
(一)活动一:指一指物体的一周
师:老师写两个字,你们说一说它是什么意思?(板书:一周)
生:指一个物体的边缘。
师拿着一个作业本:边缘?你能指一指吗?(生指)
师:她指得对不对?(对)谁还有别的想法?
生:就是一个物体的轮廓。
师拿着流动红旗:谁能指它的一周?(生指)
(二)活动二:描一描图形的一周
师:看来大家对“一周”的理解都很不错,那就拿出作业纸,你能用水彩笔描出下面各图的一周吗?
生描,师巡视并指导。
(大部分同学已完成)师:同桌之间说一说,你是怎么描的?
师拿了两位同学的作业纸放在投影仪上:我们请这两位同学上来介绍一下他们是怎么描的。
(生描完第二个图的时候)师:有没有不同的描法?
生上台展示描法。
师:你觉得他们描的有什么不一样?
生1:一个从左边开始描,一个从右边开始描。
生2:一个是一步描起来的,一个是分两步描起来的。
师:那他们俩描的有什么相同的地方?
生:都是描了图形的一周。
师:我们请女同学来描第三个图形,注意,要描出它的一周(语速慢且沉重)。(生描)
生:我有意见,角不是三角形,没有一周的。
师:你觉得三角形才有一周,给你一支笔,那你能把它变为三角形吗?
师:现在这个图形有一周了吗?
生齐答:有!
师:我们来看一下最后一个图形,先请这两位同学描一描,大家仔细观察,他们的描法一样吗?
生齐回答:不一样!
师:你同意哪位同学的描法?同桌交流一下,为什么?
生:把里面描起来就不是图形的一周了。
师:你能上来指一指哪些线指的是图形里面的线,哪些线是指图形的边线吗?(生上台指)
师对着画错的同学:你觉得自己对吗?(生摇头)没关系,刚开始学习还有点陌生,等一下就理解了。
师:刚才描的过程当中,大家都很认真,描了之后,你觉得描图形一周的过程中要注意什么?
生1:不要把里面的线也描起来。
生2:不封闭的图形没有一周。
生3:描的时候要仔细,要沿着边线描,不要描到外面去了。
课的初始,通过认识一周来唤醒学生的认知激情,因为周长这个概念的本质是一周,而学生的已有生活经验已经无意识地经历过基本过程,只是没有形成一个清晰完整的数学概念而已。所以从课的开始,通过指物体的一周、描图形的一周这两个活动逐步引入周长的本质属性,调动了学生头脑中储存的生活经验,为学生接下来的学习做好铺垫。指一指与描一描两个活动的设计,不仅为学生创设了一个探索和发现的环境,同时使每个学生都参与到探求新知的活动中,达到旧知与新知的紧密联系与结合。
二、深耕细作,争辩中提炼本质
数学的严谨性不是绝对的,一成不变的,而是相对的、发展的,体现了人类认识逐渐深化的过程。课堂中生与生的争辩不仅能激发学生的学习热情,还能在争辩过程中发现规律且提炼出概念本质。在概念教学中,教师应把握概念的操作性特点,让学生用发展的眼光来看待问题,用一定的理由来说明自己对事物或问题的见解,揭露对方的矛盾,并在争辩后达到共同的认识。在争辩中提炼本质,培养学生的辩证思维,是概念教学中应有的价值取向。
(一)活动三:发现一周的规律
师:请同学们描出下面四个图形的一周,描好后想一想,你发现了什么?
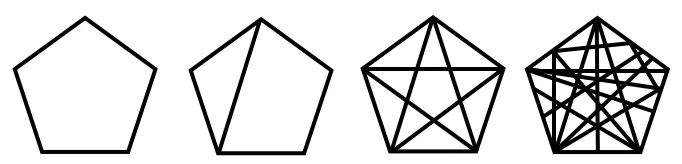
生描,师巡视并指导。
师:同桌之间说一说,你发现了什么?(同桌交流)
(请了一位同学上台)师:我们先请他介绍一下第一个图是怎么描的。
师:第二个呢?(生描)
生1:他描得不对,里面的斜线不能描起来。
生2:一周指的是外面的线,不包括里面的线。
生3:里面再多的线,我们都不能描起来。
师:你听得懂他说的意思吗?赞同吗?你能指一指剩余图形的一周吗?(生指)
师:我们还有最后一个图没有描,谁愿意上来描?
师:你发现了什么?
生1:四个图形都是五边形。
生2:图形里面有再多的线都不能算为一周。
(二)活动四:改变图形的一周
师:那我再添加一些线,图形的一周有没有改变呢?
师画,生口答。(在里面乱画)
师:你发现了什么?
生:无论里面怎么画,图形的一周都不会改变,如果画外面就可以改变了。
师:那你愿意上台来画一画吗?
师:这位同学这么画,改变图形的一周了吗?(变了)谁还愿意再来变一变?(生积极举手并上台画)
师:这么多同学画的方法,它们什么变了呢?
生1:形状变了。
生2:一周的长度变了。
生3:周长变了。
师:周长变了?那什么是周长呢?
生:一周的长度。
师(笑):你太厉害了,你的回答和书本上是一样的!大家给他点掌声。(师板书:一周的长度叫周长)
师:原来图形一周的长度就是图形的周长,周长就是我们今天学习的新知识。(板书课题)
当学生对一周有了初步的认识后,可以通过四个有联系又有区别的图形,让学生再次认识一周的本质意义。我通过让学生描一描、说一说、辩一辩、改一改、画一画等环节,经过一次次的论证,发现周长的规律是那么顺理成章。像这样的争辩环节既突出了本节课的重点,又突破了本节课的难点,提炼出周长概念的本质。
三、深图远虑,应用中探究本质
每一个数学概念都是下一个概念的基础,因此它又是具体的,概念的具体性决定了它的应用广泛性。练习的环节既是对知识巩固的环节,又是对知识与技能目标达成度实施测评的环节。教师应该利用概念具体性的特点,为学生提供认识事物数量、数形关系及转换的不同路径和独特视角。我没有设计精良的练习,而是利用教材中的教学内容,通过活动挖掘出更多的技能,让学生从不同思维解决了图形的周长的问题,让学生在应用中探究概念的本质,使学生具有数学的眼光。
活动五:数图形的周长
师:打开数学书45页的最后一题,数一数,下面图形的周长分别是多少厘米?
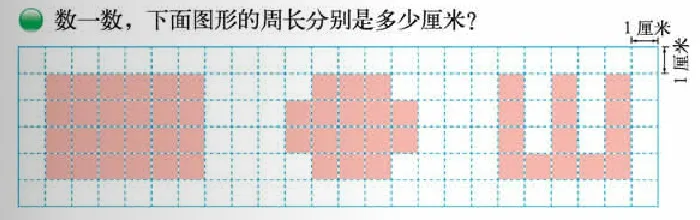
生数,师巡视并做相应的指导。生汇报。
师:我们请一位同学上台来说一说是怎么数的。
生1:我先看到右上角的标注,一格表示一厘米,然后我一边画格子,一边数,1厘米,2厘米,3厘米……19厘米,20厘米。
师:有没有不一样的方法?
生2:只要数两边就够了,因为这个图形是一个长方形,有两条长和两条宽,我们只要数一条长和一条宽就可以了。我数出来的长是6厘米,宽是4厘米,然后用6×2+4×2这个算式求出周长。
师:这位同学从长方形的特征上求出了它的周长,她的方法在今后的课中还要学习。第二个图的周长怎么求呢?
生1:第二个图,我先在角上做一个标记,然后一格一格地数。
师:这位同学在数之前做了一个记号,这个记号有什么好处?
生3:不做标记会一圈一圈不停地数。
生4:容易多数或少数,有了标记会更加清楚。
师:还有没有不同的方法?(等待了几秒钟)
生:先算出上面的两段线的长度,算式是4×2=8;再算左右两段线的长度,算式是2×2=4;接着算四个角上线的长度,算式是2×4=8;最后把它们都加起来就可以了。
师:第三个图的周长是30厘米,你们同意吗?
生:同意!
在教学中,我虽然只利用了一份材料,但是却利用这份材料挖掘出了更多的数学思维。数图形的周长,尤其是数组合图形的周长,对学生来说,一格一格地数是最容易理解的,但是很容易数错。根据学生的特点,先让学生说一说怎么数,数的时候要注意什么来加强数格子的技能。而在追问还有没有别的方法时,这样再次勾起了学生的思考,学生根据图形的特征发现规律,原来除了一格一格地数,还可以根据图形的特征,通过计算得出图形的周长,这样不仅提高了解决问题的能力,还为学习长方形的周长做好了铺垫。
四、深思长计,总结中揭示本质
课堂总结是所有教学环节的最后一部分,也是众多教学环节中比较重要的一环。如果因为教师自身感到某个数学本质不好解释,所以就放弃对它的诠释,那就放弃了一次让学生真正体验“数学化”思想的过程,失去了一次让学生数学理性思维提升的过程。可以说,好的课堂总结可以拓宽学生的视野、思维,是一个自愿拔高的行程。对于周长来自平面图形,有别于立体图形,只有在不断的疑惑与对比中,才能进一步明晰周长概念的本质属性。
活动六:指立体图形的周长
师:谁来指出这个盒子的周长?
一部分学生指了盒子其中一个面的周长,一部分学生把盒子每个面的周长都指了指。
师:为什么同一个盒子,大家指的周长却是不一样呢?(教室顿时安静了)
师指着其中一个面:如果指出盒子这个面的周长,你会指吗?
师请了几位同学指了指。
师:你有什么发现?
生1:大家指的周长都是一样的。
生2:老师让我们指指定的一个面的周长时,大家指的周长都是一样的。
生3:如果把盒子的盖子去掉,其他四个面也都去掉,只剩下最后一个面时,我们就可以指出它的周长了。
生4:如果把盒子压扁,那就可以指出它的周长了。
师:同学们真会思考,什么时候有周长,就像刚才同学们说的,把盒子压平了以后,盒子的周长就出现了,在数学中,我们叫平面图形(板书平面图形),即平面图形一周的长度叫周长。而一个盒子是立体图形,我们找出它只能每个面的周长。
大部分教师在课堂小结时都会问学生本节课学了什么,有什么收获,是对这堂课的一个总结,具有首尾呼应的作用。当我拿着一个长方体盒子时,在场的老师都“愣”住了。图形的一周不是指过了吗?图形的周长不是已经学习了吗?为什么还要回过头来重新指图形的一周呢?经过几位学生指长方体的周长出现的多种问题,让在座的学生和老师再次感受到了我对概念定义及其本质认识的深度,即平面图形一周的长度叫周长,周长的前提条件是平面图形。
数学教学是数学活动的教学,是师生之间、学生之间交往互动与共同发展的过程。纵观整堂课,我通过六个活动,在指一指、描一描、辩一辩、数一数等活动中,让学生感受到了周长的本质。我根据学生的特点引导学生发现问题、探究问题,让学生经历了旧知的唤醒、概念的本质属性从模糊到清晰,从清晰到提升,把概念教学推向了一个新的高度。

